Классфификация кинематических цепей

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ двухмассовой модели

В структурной схеме рис. 1.7 управляющим воздействием является электромагнитный момент двигателя М(р), возмущающим воздействием – статический момент Мс(р), а регулируемыми координатами (переменными состояния) – скорости первой ω₁(р) и второй ω_2­­­­­(р) масс или соответственно углы поворота φ₁(р) и φ₂(р) этих масс.

На основании этой структурной схемы можно получить передаточные функции по управляющему и возмущающему воздействиям. Получим передаточную функцию по управляющему воздействию для выходной координаты ω₂(р):

при Мс(р) =0

Передаточная функция замкнутой системы:

Получим в общем виде передаточную функцию по управляющему воздействию для выходной координаты ω₁(р):

при Мс(р) = 0

Теперь найдем передаточную функцию по возмущающему воздействию для выходной координаты ω₂(р):

при М (р) =0

, У всех один знаменатель

; обазначим:

-

где J=J₁+J₂ – суммарный момент инерции двухмассовой системы,

Ω₁₂ – собственная частота колебаний 2массовой сист..

α_В.Т – коэффициент затухания механических колебаний.

В результате получаем

В итоге получаем:

ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛОПО КРИТЕРИЮ минимум габарита ЭД

угловое ускорение:

при отсуствии нагрузки на выходном валу

фиктивный момент инее

рции

тогда следовательно

УЧЕТ ПОТЕРЬ В ПЕРЕДАЧЕ.

Потери энергии (мощности) в передаче учитывают двумя способами:

1) приближенным, т.е. с помощью КПД и 2) уточненным, т.е. непосредственным вычислением составляющих потерь. Рассмотрим эти способы.

А. Учет потерь в передачах с помощью КПД.

Механическая часть электропривода (рис.1.17) включает ротор электродвигателя ЭД с угловой скоростью w и моментом М, передаточный механизм ПМ, имеющий КПД h_п и передаточное число j, и исполнительный механизм ИМ, на валу которого приложен момент М_м и скорость вала w_м. Для наглядности обозначим статический момент в двигательном режиме , а в тормозном - . Для двигательного режима работы, исходя из закона сохранения энергии, можно записать равенство

, , где ,

- момент механизма, приведенный к валу электродвигателя.

Для тормозного режима будем иметь такое равенство

, ,

Но КПД является переменной величиной, зависящей от постоянных и переменных потерь в передаче. Определим потерю момента в передаче для двигательного режима

,

Примем допущение, что в тормозном режиме будет такая же потеря момента. Тогда статический момент в тормозном режиме можно записать в таком виде:

1) , тогда , что соответствует тормозному режиму, когда двигатель развивает тормозной момент. Применительно к грузоподъемному механизму это будет опускание тяжелого груза, когда момент от действия груза на валу двигателя М_г превышает момент потерь DМ в передаче. Получаем так называемый тормозной спуск;

2) , тогда , что соответствует не тормозному, значит, двигательному режиму. Для грузоподъемного механизма это эквивалентно опусканию крюка, когда момент от его веса на валу двигателя М_К меньше момента потерь DМ в передаче. Имеем так называемый силовой спуск.

Потери момента в передаче приближенно выражаются через две составляющие, одна из которой для данной передачи является постоянной величиной, а вторая – пропорциональна передаваемому моменту:

,

где – коэффициент постоянных потерь;

b – коэффициент переменных потерь;

М_с.ном – номинальный статический момент передачи;

М_перед – передаваемый момент, который равен моменту на выходном (по направлению передачи энергии) валу передачи.

Для установившегося двигательного режима . КПД передачи можно представить отношением мощностей в установившемся режиме:

,

где , ,

P₂ – мощность на выходном валу ПМ в установившемся двигательном режиме;

DP – потери мощности в передаче.

, Обозначим , ,

При номинальной нагрузке К_З=1 и

, ,

Таким образом, КПД передачи является функцией коэффициента загрузки и номинального КПД, так как коэффициент постоянных потерь зависит от номинального КПД и для ряда передач приводится в справочниках.

14. Уточненный метод учета потерь в передаче.

Рассмотрим сначала установившийся режим работы. Для двигательного установившегося режима имеем:

, ,

Для тормозного установившегося режима (см. Рис.1.17):

,

,

откуда

,

Теперь перейдем к переходным режимам. Для двигательного режима в переходном процессе (разгон)

,

, находим ,

где ,

- коэффициент, учитывающий момент инерции передаточного механизма;

- момент инерции ротора электродвигателя;

- эквивалентный статический момент при разгоне электропривода;

- эквивалентный момент инерции при разгоне электропривода.

Для тормозного режима в переходном процессе

,

где М – момент электродвигателя в переходном процессе,

, ,

находим , где ,

- эквивалентный статический момент при торможении электропривода;

- эквивалентный момент инерции при торможении электропривода.

Заметим, что эквивалентные статические моменты при разгоне и торможении электропривода равны статическим моментам для установившихся двигательного и тормозного режимов. Самое важное состоит в том, что непосредственный учет потерь в передаче привел к тому, что эквивалентный момент инерции при разгоне электропривода стал больше, а при торможении меньше суммарного момента инерции электропривода. Получилось, что инерционность электропривода зависит, при прочих неизменных условиях, от режима работы.

Сложность непосредственного расчета потерь в передаче состоит в том, что необходимо иметь значения коэффициентов и b.

ПРЯМЫЕ И ОБРАТНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ ДЛЯ СТАТОРА И РОТОРА ОЭМ

Преобразование, с помощью которого координаты точки А в новой системы координат выражаются через координаты x_А,y_А этой точки в старой системе координат, называется прямым координатным преобразованием. Из геометрических построений на Рис. 2.3 следует, что

Под вектором будем понимать вектор любой переменной ОЭМ, например, вектор напряжения , вектор тока , вектор потокосцепления . Под координатными осями будем понимать:

где оси u, вращаются с постоянной угловой скоростью w_К­­­ относительно неподвижных осей 1a-1b.

Угол поворота осей u, относительно неподвижных осей 1a-1b равен

j_К=w_К t (2.48)

где t – время.

Теперь, после оговоренных условий, можем записать уравнения координатных преобразований для вектора любой переменной ОЭМ:

Прямые преобразования:

а) для переменных статора: б) для переменных ротора:

(2.49) (2.50)

Обратные преобразования: б) для переменных ротора:

а) для переменных статора:

(2.51) (2.52)

где , – проекции вектора на оси координат 1a-1b ,

, – проекции вектора на оси координат 1u-1 ,

, – проекции вектора на оси координат 2d-2q,

, – проекции вектора на оси координат 2u-2 .

Для упрощения дальнейших записей обозначим:

,(2.53); ,(2.54)

,(2.55); ,(2.56)

,(2.57)

где – матрица поворота осей координат статора,

– обратная матрица поворота осей статора,

– матрица поворота осей координат ротора,

– обратная матрица поворота осей координат ротора,

Можно видеть, что

= = ,

= = ,

т. е. обратные матрицы поворота равны транспонированным матрицам. После введения этих обозначений можем записать:

Прямые преобразования: Обратные преобразования:

а) для переменных статора: а) для переменных статора:

(2.58) (2.60)

б) для переменных ротора: б) для переменных ротора: (2.59) (2.61)

Из (2.96) определяем

(2.117)

и подставляем в (2.111):

(2.118)

так как =0.

Используя (2.96) ), выражаем

(2.119)

и подставляем в (2.111):

(2.120)

где Kr = ,(2.121) Kr – коэффициент магнитной связи ротора.

Теперь из (2.95) ) находим

(2.122) и подставляем в (2.111):

где Ks = , (2.124) Ks – коэффициент магнитной связи статора.

Из (2.95) и (2.96) следует, что

(2.125)

Поскольку

, (2.153)

то

, (2.154)

где - индуктивные сопротивления рассеяния статора, ротора (приведенное) и намагничивающего контура.

Уравнениям (2.154) соответствует эквивалентная схема ОЭМ, показанная на Рис.2.7, причем

(2.155)

- комплекс ЭДС, индуктированной потокосцеплением взаимоиндукции.

ФАЗНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ

В связи с тем, что большинство электрических машин переменного тока выполняется трехфазными, возникает задача преобразования переменных (напряжений, токов, потокосцеплений) реальной трехфазной машины в переменные двухфазной обобщенной машины. Необходимо также производить и обратные преобразования переменных двухфазной машины в переменные трехфазной машины. При этом все преобразования должны быть инвариантными по мощности.

Рассмотрим сначала преобразование переменных трехфазной электрической машины в переменные двухфазной обобщенной машины. Будем полагать, что переменные и пропорциональны переменным и соответственно. Обозначим коэффициент пропорциональности .

Переменные по осям и могут иметь любую величину, соответственно и по осям .

Совместим ось обмотки статора с осью (Рис.2.8). Отметим углы оси по отношению к осям : и углы оси по отношению к осям : .

В результате можем составить матрицу поворота трехфазных осей к двухфазным:

, (2.156)

Теперь переменные статора двухфазной системы можно выразить через переменные трехфазной системы:

(2.157)

где , (2.158)

Учитываем, что

, (2.167)

, (2.168)

, (2.169)

тогда

, (2.170)

Вычислим произведение матриц:

Следовательно

, (2.171)

Из условия инвариантности следует принять

, (2.172) откуда , (2.173)

Но существует и другой подход к фазным преобразованиям, предложенный Ковачем и Рацем […]. Сущность его состоит в том, что в преобразованиях переменных от трехфазной машины к двухфазной и наоборот переменные одной фазы, например фазы (фазы ) не изменяются. Тогда при переходе от трехфазной машины к двухфазной следует взять :

, (2.174)

Для соблюдения инвариантности мощности необходимо в этом случае в формулах мощности и электромагнитного момента использовать коэффициент : , (2.175) ,(2.176)

При переходе от двухфазной машины к трехфазной в преобразованиях переменных принимают коэффициент :

, (2.177)

Если трехфазная машина имеет переменную нулевой последовательности (четырехпроводная система), то , (2.178)

и , (2.179)

При наличии нулевой последовательности в токах и напряжениях в четырехпроводной системе будет потребляться мгновенная мощность

,

Где - соответственно нулевая последовательность напряжения и тока.

35. Инвариантность мощности в преобразованиях уравнений ОЭМ от осей 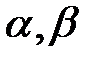к осям u-v

(2.81)

Уравнения (2.81не имеют периодически изменяющихся коэффициентов, хотя остаются нелинейными, так как имеют произведения переменных величин ( и y). Вместе с тем в этих уравнениях появляются составляющие ЭДС, связанные с вращением системы координат u- относительно исходной системы координат 1a-1b. Указанные уравнения соответствуют другой модели ОЭМ, где на взаимно перпендикулярных осях u- находятся неподвижные относительно друг друга системы обмоток, которые вращаются со скоростью относительно осей 1a-1b. Возникающие при таком вращении дополнительные ЭДС и обеспечивают инвариантность мощности при преобразованиях переменных. Покажем, что при рассмотренном координатном преобразовании соблюдается инвариантность мощности. В целях упрощения примем u_2d=u_2q=0, тогда полная мощность S:

(2.83)

Представим векторы напряжения и тока через обратные преобразования (2.63), (2.64) и учтем, что

, (2.84)

тогда

так как (2.86)

Равенство (2.87)

подтверждает инвариантность мощности при координатном преобразовании.

36 РЕЖИМЫ РАБОТЫ ЭЛЕКТРОДВИГАТЕЛЕЙ и ограничения на электромеханические преобразования энергии

Электрическая машина обратима, поэтому она может работать в двух режимах, двигательном итормозном. В двигательном режиме электромагнитная мощность принимается положительной (Р_эм = Мw >0), а в тормозном режиме -отрицательной (Р_эм = Mw < 0).

Каждый тормозной режим является генераторным, так как энергия поступает в электрическую машину с вала, преобразуется в электрическую, отдается в сеть или рассеивается в сопротивлениях, связанных с якорем. Различают три тормозных режима электрической машины:

1) Рекуперативное торможение,т. е. генераторный режим работы электрической машины параллельно с сетью. В этом ре­жиме к двигателю поступает ме­ханическая энергия, которая за вычетом потерь возвращается в сеть в виде электрической энергии (рис. 3.2).

2) Торможение противовключением,т. е. генераторный режим работы электрической машины последовательно с сетью. В режиме противовключения к электрической машине с одной стороны подводится механическая, ас другой - электрическая энергия, и суммарная энергия превращается в потери (рис. 3.3).

3) Динамическое торможение, т. е. генераторный режим работы электрической машины неза­висимо от сети. В этом режиме подводимая к валу механическая энергия преобразуется в электрическую, а затем выделяется в виде потерь (рис. 3.4).

Электромеханическое преобразование энергии сопровождается потерями, которые выделяются в виде тепла в соответствующих ча­стях электрической машины и вы­зывают ее нагревание. Нагревание электрической машины ограничи­вается допустимой температурой. Поэтому первым ограничением преобразования энергии в электродвигателе будет ограничение по нагреву: мощность, момент и ток двигателя не должны превышать значений, допустимых по нагреву. До­пустимые по условиям нагрева дан­ные электродвигателя называются ) номинальными.

Второе ограничение, связанное с преобразованием энергии электродвигателем, состоит в кратковременно допустимом токе и моменте: I_доп, М_доп, которые электродвигатель может безопасно выдерживать заданное время. Отношение этих величин к номинальным называют перегрузочной способностью двигателя.

Для коллекторных машин перегрузочная способность ограничивается в первую очередь условиями коммутации. Реактивная ЭДС в коммутирующей секции обмотки якоря, которая определяет искрение на коллекторе, пропорци­ональна произведению скорости со и тока якоря I. В связи с этим, исходя из допустимой степени искрения на коллекторе, в диапазоне скоростей w > w_ном следует уменьшать допустимое значение тока:

Для обычных двигателей постоянного тока при номинальной скорости

Третье ограничение при преобразовании энергии электродвигателем связа-ю с допустимой скоростью изменения тока. В коллекторных машинах для улуч­шения условий коммутации применяют добавочные полюса. Из-за магнитной инерционности искрение на коллекторе зависит от скорости изменения тока якоря. Для нормальной работы коллекторной электрической машины необхо­димо, чтобы выполнялось условие:

Следует заметить, что ограничение на скорость изменения тока существует и всиловых полупроводниковых приборах, например, тиристорах, хотя она там на порядки выше, чем в двигателях постоянного тока, для которых обычно

В бесколлекторных маши­нах переменного тока (асинх­ронных, синхронных) пере­грузочная способность выше, чем в коллекторных машинах, и ограничивается наибольшим (критическим) моментом, ко­торый может развивать маши­на при данном напряжении и токе возбуждения. •

Максимальное значение скорости двигателя ограничи­вается механической прочно­стью подшипниковых узлов и креплений ротора, а для кол­лекторных машин - главным образом, допустимым значени­ем реактивной ЭДС.

Теперь можно на плоско­сти переменных о)-М выделить облает допустимых значений для длительной и кратковре­менной работы электродвигателя (рис. 3.5),

37. МОДЕЛЬ ДПТ НВ В ОСЯХ И ЕЁ УРАВНЕНИЯ

Модель обобщенной электрической машины в осях 1α-1β, 2d-2q включает в себя все частные модели электрических машин. Модель ДПТ НВ получается из этой модели с помощью следующих изменений:

1) Обмотка статора по оси 1β включается на постоянное напряжение, а обмотка статора по оси 1α не используется;

2) Обмотки фаз 2d, 2q питаются переменными токами i_2d, i_2q от преобразователя частоты ПЧ, осуществляющего коммутацию тока в функции электрического угла φ_ЭЛ поворота ротора с угловой частотой ω_ЭЛ, где сигнал φ_ЭЛ поступает от датчика положения ротора ДПР (рис.3.6).

Если ПЧ – вентильный преобразователь частоты коммутируемый с помощью ДПР, то эта модель соответствует модели вентильного (электроннокоммутируемого) двигателя. Если же ПЧ – механический коммутатор, т.е. коллектор со щетками, то рис. 3.1 представляет собой модель коллекторного двигателя постоянного тока.

Для двухфазной модели обобщенной электрической машины в осях 1α-1β, 2d-2q была получена формула (2.25) мгновенного значения электромагнитного момента

В представленной на рис. 3.6 модели ДПТ НВ U₁α=0, i₁α=0, поэтому

(3.5)

Для непрерывного преобразования энергии электродвигателем необходимо, чтобы электромагнитный момент (3.5) не зависел от положения ротора, т.е. от φ_ЭЛ. Это возможно, если

(3.6)

тогда

(3.7)

Преобразуем токи ротора i_2d, i_2q к неподвижным осям α-β, используя общие формулы (2.50) прямого преобразования переменных ротора:

(3.8)

где Δφ_К=φ_К-φ_ЭЛ=(ω_К-ω_ЭЛ)t

Для неподвижных осей α-β имеем ω_К=0 и

Δφ_К=-ω_ЭЛt=-φ_ЭЛ (3.9)

тогда с учетом (3.6) и (3.9) имеем

(3.10)

т.е. i_2α=i_Я и i_2q=0.

Следовательно, две обмотки ротора, находящиеся на осях 2d-2q, при преобразовании к осям статора дают одну обмотку, оп которой протекает постоянный ток iя.

38. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДПТ НВ И СТРУКТУРНАЯ СХЕМА ДПТ НВ В ОСЯХ

Уравнение обобщенной электрической машины в осях α-β применительно к условиям ДПТ НВ:

(3.12)

Имеют вид

(3.13)

Учитывая, что

(3.14) пол-ем (3.15)

Изменяя обозначения переменных обобщенной электрической машины в осях α-β на привычное обозначение переменных ДПТ НВ:

(3.16) то (3.17)

Обозначим:

(3.18)

(3.19)

где е – ЭДС вращения ДПТ НВ,

Ф – магнитный поток взаимоиндукции,

k – конструктивный коэффициент определяемый как

(3.20)

N – число активных проводников обмотки якоря,

а – число пар параллельных ветвей обмотки.

На основании (3.19) имеем

(3.21)

где

(3.22)

L_Ф – эквивалентная индуктивность, определяющая связь между магнитным потоком взаимоиндукции и током возбуждения электрической машины.Величину L_Ф можно определить из кривой намагничивания электрической машины (рис. 3.9).

Теперь систему уравнений (3.17) можно записать в виде:

(3.23)

Выразим

(3.24)

и подставим в первое уравнение (3.23):

(3.25)

Обозначим

(3.26) (3.27)

тогда (3.23) можно представить в таком виде

(3.28)

где Т_В – электромагнитная постоянная времени цепи возбуждения ДПТ НВ,

Т_Я – электромагнитная постоянная времени якорной цепи.

Систему уравнений (3.28) запишем в операторной форме

(3.29)

УЧЕТ ПОТЕРЬ В ПЕРЕДАЧЕ 18

14. Уточненный метод учета потерь в передаче. 20

ПРЯМЫЕ И ОБРАТНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ ДЛЯ СТАТОРА И РОТОРА ОЭМ 42

ПРЕОБРАЗОВАНИЕ ПЕРЕМЕННЫХ ЭЛЕКТРИЧЕСКОГО РАВНОВЕСИЯ ДЛЯ ОБМОТОК СТАТОРА И РОТОРА ОЭМ

ФАЗНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ 56

35. Инвариантность мощности в преобразованиях уравнений ОЭМ от осей 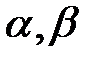к осям u-v 62

ТОРМОЗНЫЕ РЕЖИМЫ ДПТ СВ

51.ЛИНЕАРИЗОВАННАЯ СТРУКТУРНАЯ СХЕМА АД ПРИ R1=0

КЛАССФИФИКАЦИЯ КИНЕМАТИЧЕСКИХ ЦЕПЕЙ

Номинальная мощность электродвигателя Р_ном определяется выражением

Р_ном=М_номw_ном , (1.1)

где М_ном , w_ном – номинальные вращающий момент и угловая скорость ротора.

В свою очередь

М_ном=С_кD­ l (1.2)

где

С_к – коэффициент, зависящий от конструктивных особенностей электрической машины,

D – диаметр якоря,

L – длинна активной части якоря.

Отсюда следует, что для уменьшения габаритов электродвигателя (D­ l) при заданной номинальной мощности Р_ном необходимо увеличивать угловую скорость w_ном , особенно для маломощных двигателей (w_ном=100 – 600 рад/с). В тоже время для рабочих машин по технологическим условиям требуется значительно меньшая скорость, примерно, в 10 – 100 раз меньшая. Согласование механических параметров электродвигателя (скорости и момента) с механическими параметрами рабочей машины осуществляется с помощью передаточного механизма (ПМ). При этом ПМ могут изменять не только количественные параметры механической энергии, но и характер движения, преобразуя вращательное движение в поступательное.

Редукторы представляют собой зубчатые передачи, заключенные в единый корпус (Рис.1.1а). По числу зубчатых пар они разделяются на одно-, двух-, трех-, n-ступенчатые. По виду зубьев: на прямозубые, косозубые, червячные. По исполнению: на цилиндрические и конические. По принципу действия: на обычные и планетарные.

Редуктор характеризуется передаточным числом

Совместная компоновка электродвигателя и редуктора называется мотор-редуктором.

Передаточные числа редукторов находятся в пределах =1,6 – 12500. редукторы изготовляются на мощности от 0,12 до 560 кВт и выходные моменты до 1200кНм.

Ременные(цепные)передачи(Рис.1.1б) характеризуются передаточным числом

где D₁, Z₁ – диаметр (число зубьев) входного шкива (звездочки),

D₂, Z₂ – диаметр (число зубьев) выходного шкива (звездочки).

Передачизубчатоеколесо-рейка, барабан-трос преобразуют вращательное движение в поступательное и характеризуются радиусом приведения

Винтоваяичервячно-реечнаяпередачи преобразуют вращательное движение винта (червяка) в поступательное перемещение гайки (рейки). Радиус приведения поступательного движения к вращательному:

а) для винтовой передачи

,

б) для червячно-реечной передачи

где l, – линейные перемещения и скорость,

,