Определение коэффициента внутреннего трения жидкости
Цель работы: определение коэффициента внутреннего трения (вязкости) различных жидкостей двумя методами: методом Стокса[5] и методом сравнения.
Теоретическая часть
При движении жидкости между ее соседними слоями, имеющими различные скорости, возникают силы внутреннего трения (вязкости), направленные по касательной к поверхности слоев. Величина этих сил зависит от рода жидкости, от разности скоростей и расстояния между слоями и определяется формулой Ньютона:
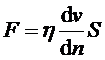, (1)
где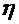 
- коэффициент внутреннего трения жидкости, 
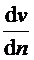- абсолютная величина градиента скорости, S- площадь поверхности взаимодействующих слоев жидкости.
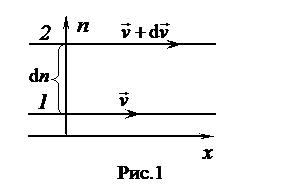Рассмотрим жидкость, движущуюся в направлении оси x (рис. 1). Пусть скорость слоя (1) равна 
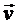, скорость слоя (2)равна 
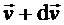, кратчайшее расстояние между слоями 
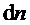. Абсолютная величина градиента скорости 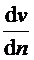определяет быстроту изменения скорости жидкости от слоя к слою в направлении нормали к слоям.
Коэффициент внутреннего трения 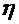зависит от природы жидкости и от ее термодинамического состояния. Его называют также коэффициентом вязкости. Динамический коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу поверхности слоя при единичном градиенте скорости. В СИ единицей динамического коэффициента вязкости является 1(Н/м2)∙с=1Па∙с (паскаль-секунда). Помимо динамического коэффициента вязкости часто пользуются кинематическим коэффициентом вязкости 
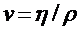, где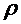 
- плотность жидкости.
Метод Стокса
Действие сил внутреннего трения появляется при движении тел в жидкости. При малых скоростях и обтекаемой форме тела,когда не возникает вихрей, сила сопротивления обусловлена исключительно вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твердому телу, увлекается им полностью. Следующий слой увлекается за телом с меньшей скоростью. Таким образом, между слоями возникают силы сопротивления. В 1851 г. английский физик Д.Г. Стокс вывел формулу для силы сопротивления, действующей на твердый шар при его медленном равномерном поступательном движении в неограниченной жидкости:
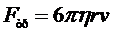, (2)
где 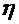– динамический коэффициент вязкости, 
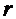– радиус шара, 
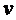- скорость шара относительно жидкости.
Пусть шарик радиусом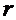 
изготовленный из материала плотностью 
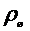, падает в исследуемой жидкости плотностью 
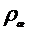. На него будут действовать три силы: сила тяжести, направленная вниз:
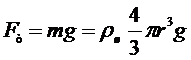, (3)
( 
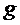- ускорение свободного падения) выталкивающая архимедова сила, направленная вверх:
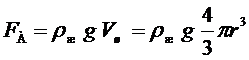, (4)
и сила внутреннего трения (2), также направленная вверх. Силы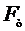 
и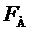 
не зависят от скорости шарика (постоянны), а сила 
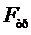увеличивается по мере увеличения скорости шарика. При некоторой скорости 
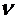наступает равновесие сил, т.е. шарик движется с постоянной скоростью 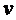(уставившееся движение). Тогда, применяя второй закон Ньютона, получаем выражение для модуля сил:
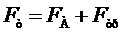. (5)
Подставим формулы (2), (3) и (4) в формулу (5):
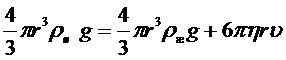, (6)
откуда:
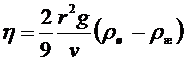. (7)
Это уравнение справедливо только тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубы радиусом R, то приходится учитывать влияние стенок трубы. C учетом поправок формула для определения коэффициента вязкости принимает следующий вид:
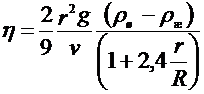. (8)
Экспериментальная часть