Закон Ампера. Взаимодействие параллельных токов

Ампер установил, что сила d 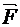, с которой магнитное поле действует на элемент проводника 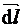с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию:

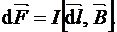. (3.12)

Направление вектора d 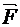может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор ,а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера вычисляется по формуле

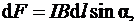(3.13)

где 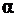– угол между векторам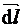и и .

Закон Ампера применяется для определения силы взаимодействия двух токов.

Действие магнитного поля

На движущийся заряд

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью 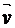, называется силой Лоренцаи выражается формулой

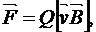(3.14)

где –индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки:если ладонь левой руки расположить так, чтобы в нее входил вектор ,а четыре вытянутых пальца направить вдоль вектора 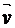, то отогнутый большой палец покажет направление силы, действующей на положительный заряд (рис. 3.7) .

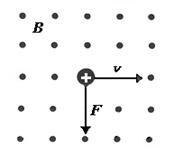
Рис. 3.7

Модуль силы Лоренца

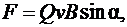
, (3.15)

где a – угол между 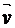и .

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Если на движущийся электрический заряд помимо магнитного поля с индукцией действует и электрическое поле с напряженностью 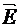, то результирующая сила 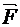, приложенная к заряду, равна векторной сумме сил – силы, действующей со стороны электрического поля, и силы Лоренца:

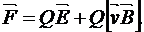. (3.16)

Это выражение называется формулой Лоренца. Скорость 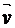в этой формуле есть скорость заряда относительно магнитного поля.

Если заряженная частица движется в магнитном поле со скоростью 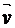вдоль линий магнитной индукции, то угол aмежду векторам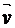и и равен 0 или p. Тогда по формуле (3.15) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует, и она движется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью 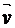, перпендикулярной вектору ,то сила Лоренца постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия

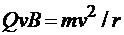
откуда

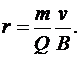(3.17)

Период вращения частицы,т. е. время Т, одного полного оборота,

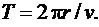
Подставив сюда выражение (3.17) получим

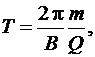(3.18)

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при 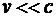). На этом основано действие циклических ускорителей заряженных частиц.

Если скорость 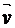заряженной частицы направлена под углом a к вектору В(рис. 3.8), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v_װ 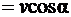;2) равномерного движения со скоростью 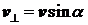по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (3.17) (в данном случае надо заменить v на 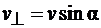). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (cм. рис. 3.8). Шаг винтовой линии

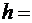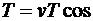v_װ a

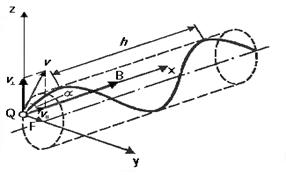
Рис. 3.8

Подставив в последнее выражение (3.8), получим

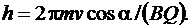(3.19)

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость 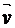заряженной частицы составляет угол a с направлением вектора неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.

Эффект Холла

Эффект Холла (1879) – это возникновение в металле (или полупроводнике) с током плотностью 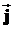, помещенном в магнитное поле ,электрического поля в направлении, перпендикулярном и .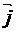

Поместим металлическую пластинку с током плотностью 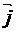в магнитное поле ,перпендикулярное 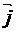(рис. 3.9). При данном направлении 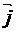скорость носителей тока в металле – электронов – направлена справа налево. Электроны испытывают действие силы Лоренца, которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникнет повышенная концентрация электронов (он зарядится отрицательно), а у нижнего – их недостаток (зарядится положительно). В результате этого между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность E_B этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, установится стационарное распределение зарядов в поперечном направлении. Тогда

eЕ_В 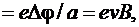или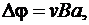

где a – ширина пластинки, Dj – поперечная (холловская) разность потенциалов.

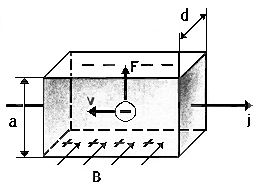
Рис.3.9

Учитывая, что сила тока 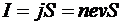( 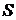– площадь поперечного сечения пластинки толщиной d, n – концентрация электронов, v – средняя скорость упорядоченного движения электронов), получим

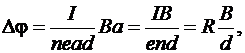(3.20)

т. е. холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d.

В формуле (3.20) 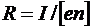– постоянная Холла,зависящая от вещества. По измеренному значению постоянной Холла можно: 1) определить концентрацию носителей тока в проводнике (при известных характере проводимости и заряде носителей); 2) судить о природе проводимости полупроводников, так как знак постоянной Холла совпадает со знаком заряда е носителей тока. Эффект Холла поэтому – наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется также для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т. д.

3.6. Циркуляция вектора для магнитного

Поля в вакууме

Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Циркуляцией вектора по заданному замкнутому контуру называется интеграл

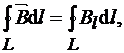
где dl – вектор элементарной длины контура, направленный вдоль обхода контура, 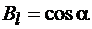– составляющая вектора в направлении касательной к контуру (с учетом выбранного направления обхода) a – угол между векторами и d .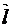

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной 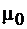на алгебраическую сумму токов, охватываемых этим контуром:

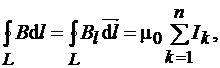(3.21)

где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным; например, для системы токов, изображенных на рис. 3.10.

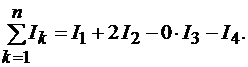(3.22)

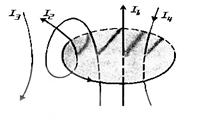
Рис. 3.10

Выражение (3.21) справедливо только для поля в вакууме, поскольку, как будет показано, для поля в веществе необходимо учитывать молекулярные токи.

Продемонстрируем справедливость теоремы о циркуляции вектора на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам (рис. 3.11).

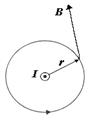
Рис.3.11

Представим себе замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора равна

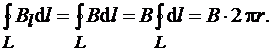
Согласно выражению (3.21),

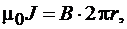
откуда

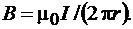(3.23)

Сравнивая выражения (1.21) и (3.21) для циркуляции векторов Еи ,видим, что между ними существует принципиальное различие. Циркуляция вектора 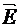электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био – Савара – Лапласа.