Уравнение неразрывности для элементарной струйки (уравнение расхода для элементарной струйки).

δQ = V₁ *δS₁ = V₂ *δS₂ → const (вдоль струйки),(5.3)

где V₁ , V₂ – мгновенные скорости в сечениях .

Уравнение неразрывности (расхода) для потока, ограниченного непроницаемыми стенками (уравнение расхода для потока).

Q = V_ср1 *S₁ = V_ср2 *S₂ → const (вдоль потока),(5.4)

где V_ср1 , V_{ср2 -} средние скорости.

Из уравнения расхода для потока следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:

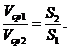
Уравнение расхода является следствием закона сохранения вещества.

5.4. Уравнение Бернулли для элементарной струйки идеальной жидкости.

При выводе уравнения Бернулли рассматривается установившееся течение идеальной жидкости под действием только силы тяжести.

Уравнение Бернулли связывает давление и скоростьидеальной жидкости для установившегося течения.

Возьмем одну из элементарных струек (рис.5.4), составляющих поток, выделим сечениями 1-1и 2-2участок этой струйки произвольной длины.

Площадь первого сечения равна - δS₁, скорость в нем - V₁ , давление – P₁, а высота относительно плоскости сравнения - Z₁.

Во втором сечении δS₂, V₂ , P₂ и Z₂.

За малый отрезок времени δt выделенный участок струйки переместится в положение 1' – 2'.

Применим к массе жидкости в объеме элементарной струйки теорему об изменении кинетической энергии: работа сил, приложенных к телу, равна приращению кинетической энергии этого тела:

δА_Р+G = δm[(V₂²)/2 - (V₁²)/2]

На жидкость действуют силы тяжести и силы давления, нормальные к поверхностям сечений рассматриваемого участка струйки.

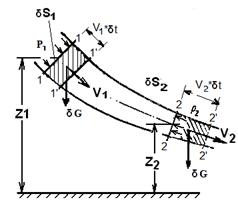
Рис.5.4.Вывод уравнения Бернулли

Определим работу сил давления, сил тяжести и изменение кинетической энергии участка струйки за время δt.

Работа силы давления жидкости в первом сечении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p₁*δS₁ на перемещение V₁δt:

А₁ = (p₁*δS₁)*(V₁δt)

Работа силы давления жидкости во втором сечении отрицательна, так как направление силы противоположно направлению перемещения, и определяется выражением (силы давления жидкости являются сжимающими)

А₁ = - (p₂*δS₂) *(V₂δt).

Силы давления жидкости, действующие по поверхности струйки, работы не производят, так как они нормальны к перемещениям.

Работа сил давления

δA_P = (p₁*δS₁) *( V₁δt) - (p₂*δS₂) *(V₂δt). (5.5)

Работа силы тяжести равна изменению потенциальной энергиивыделенного объема струйки. Из потенциальной энергии жидкости в объеме 1 - 2 вычтем потенциальную энергию жидкости в объеме 1’- 2’. При этом энергия промежуточного объема 1’- 2 сократится, и останется лишь разность потенциальной энергии элементов 1- 1’, 2- 2’.

По уравнению расходов (закон неразрывности) элементарные объемы δW и силы тяжести заштрихованных элементов 1 -1’ и 2 - 2’ равны между собой:

δW=V₁*δS₁*δt = V₂*δS₂*δt

δG = ρ*g* V₁*δS₁*δt = ρ*g* V₂*δS₂*δt . (5.6)

Работа силы тяжести будет равна произведению разности высот на силу тяжести δG:

δA_G = δG*(z₁-z₂). (5.7)

Приращение кинетической энергии участка струйки за время δt равно разности кинетической энергии объема 1’- 2’ и кинетической энергии объема 1 - 2. При вычитании кинетическая энергия промежуточного объема 1’ - 2 сократится, и останется разность кинетических энергий элементов 1 -1’ и 2 - 2’, масса каждого из которых равна δm = δG/g.

Таким образом, приращение кинетической энергии струйки

(V₂²- V₁²)* δG/(2g), (5.8)

Сложив работу сил давления (5.5) с работой силы тяжести (5.7) и, приравняв эту сумму приращению кинетической энергии (5.8), получим исходное уравнение

(p₁*δS₁) *( V₁δt)— (p₂*δS₂) *( V₂δt) +(z₁-z₂) *δG=(V²₂- V²₁)*δG/(2g). (5.9).