Силы давления жидкости, действующие на грани нормальные к осям

Оx:δР_х= р_х*δS_x, площадь грани - δS_x= (δyδz/2)=δS_n* Cos(n ^x),

Оу: δР_у = р_у*δS_у, площадь грани - δS_у= (δхδz/2),

Оz: δР_z = р_z*δS_z, площадь грани - δS_z= (δxδy/2),

на наклонную грань: δР_n= р_n*δS_n,

проекция суммарной массовой силы на ось Ох: δF_x =Xδm= Х [ρ(δxδyδz/6)].

На остальные оси проекции массовой силы Y и Z могут быть записаны в таком же виде.

Составим уравнение равновесия тетраэдра под действием поверхностных и массовых сил в проекциях на ось Ох, учитываем допущение о том, что силы давления жидкости направлены по нормалям к соответствующим площадкам. Проекция сил на ось Ох

δР_х – δР_n + Хδm = 0.

Выразим проекцию силы давления жидкости в этом уравнении через произведение давления на площадь, проекцию массовой силы через произведение проекции ускорения (единичной массовой силы) на массу

р_х(δyδz/2) –р_n[δS_n*Cos(n^x)] + Х*[ρ(δxδyδz/6)] = 0. (2.1)

где Cos(n ^x) –косинус между нормалью к площадкеδSnи осьюОх, δm = ρδW=(δxδyδz/6) - масса жидкости в тетраэдре, W = δxδyδz/6 -объем тетраэдра.

Разделив уравнение (2.1) на площадь треугольника δyδz/2, которая равна проекции площади наклонной грани δS_n на плоскость у0z, т. е. δS_n*Cos(n^x) = δSх =δyδz/2, получим

р_х –р_n + X [ρ(δx) /3] =0.

При стремлении объема тетраэдра к нулю, δx, δy, δz также стремятся к нулю. Поэтому последний член уравнения, содержащий множитель δx, стремится к нулю.

Давления р_х и р_n будут стремиться к значениям гидростатического давления в вершине трехгранного угла тетраэдра. При переходе к пределу при δх→0, получим

р_х - р_n = 0 или р_х = р_n.

Аналогично, составляя уравнения равновесия вдоль осей Оу и Оz, находим

р_х = р_у = р_z= р_n

Так как размеры тетраэдра δx, δy, δz взяты произвольно, и наклон площадки δS также произволен и, следовательно, в пределе при стремлении объема тeтраэдра к нулю, давление в его вершине по всем направлениям будет одинаково.

Закон Паскаля: В объеме покоящейся жидкости величина гидростатического давления в точке не зависит от направления площадки, для которой она вычислена. И раз не зависит, значит - скаляр.

Это свойство гидростатического давления имеет место не только при покое, но и при движении идеальной жидкости.

При движении реальной жидкости, обладающей вязкостью, возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством не обладает.

Основное уравнение гидростатики

Рассмотрим равновесие жидкости, когда на нее действует одна массовая сила — сила тяжести. На свободную поверхность жидкости, содержащейся в сосуде (рис.2.4), действует давление Р₀. Найдем гидростатическое давление р в произвольно взятой точке М, расположенной на глубинеh.

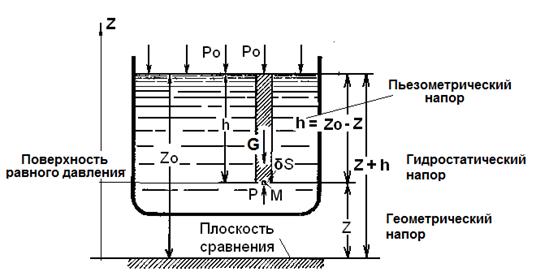
Рис.2.4 Вывод основного уравнения гидростатики. Z –геометрический напор, Zo-Z –пьезометрический напор, Z+h – гидростатический напор.

Выделим около точки М элементарнyю горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем высотой h, воспользуемся «принципом отвердевания» и получим условия равновесия выделенного объема. Сила тяжести G выделенного объема направлена вниз.

Вес жидкости G будет удерживаться силой, действующей на нижнее основание цилиндра и направленной вверх. Это будет сила давления жидкости, которая является внешней по отношению к этому объему.

Запишем условие равновесия выделенного объема в проекции на вертикальную ось. Р и Ро – давления, δS – площадь основания объема, h – высота столба, ρg(h*δS)- вес объема

РδS –P₀δS – ρg(h*δS) = 0 .

вес

Силы давления по боковой поверхности цилиндра в уравнение не входят, так как они нормальны к вертикальной оси. Сократив выражение на δS, найдем

Основное уравнение гидростатики: Р=Р₀+ρgh (2.2.)

Используя его можно определить давление в любой точке покоящейся жидкости. Это давление складывается из давления Р₀на внешнюю поверхность жидкости и давления, вызываемого весом выделенного объема жидкости, опирающегося на δS.

Давление Р₀ является одинаковым для всех точек объема жидкости, поэтому это давление, приложенное к внешней поверхности жидкости, передается во все точки объема и по всем направлениям одинаково.

Давление жидкости как видно из формулы (2.2.) возрастает при увеличении глубины по линейной зависимостии на данной глубине есть величина постоянная.