Формальные представления об активности ионов в растворах электролитов
В первой части «Курса физической химии» было введено понятие о термодинамической активности как о величине, заменяющей молярную долю в уравнении для химического потенциала вещества в конденсированной системе (ч.1, стр. 71):
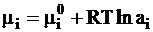 . (4 - 1)
. (4 - 1)
Формально активность вещества можно представить как произведение молярной доли вещества xi на некоторую величину f, называемую коэффициентом активности:
ai = fi×xi . (4 - 2)
При изучении термодинамических свойств растворов кроме молярной доли для выражения содержания растворенного вещества может быть использована молярная концентрация Сi или моляльность mi раствора. В связи с этим можно использовать три типа активности и соответственно три типа коэффициентов активности, которые связаны с молярными долями, молярностью и моляльностью следующими уравнениями:
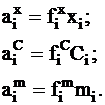
 (4 - 3)
(4 - 3)
Коэффициенты активности определяют экспериментально, используя данные по коллигативным свойствам растворов (осмотическому давлению, понижению давления пара растворителя, повышению температуры кипения и понижению температуры замерзания). Для неэлектролитов не существуют принципиальные трудности, связанные с обработкой экспериментальных данных, так как они относятся только к одному сорту частиц - молекулам растворенного вещества. В растворах электролитов, напротив, существует несколько сортов частиц (катионы, анионы) и такие характеристики раствора, как понижение температуры плавления, повышение температуры кипения, относятся одновременно ко всем частицам. По этой причине экспериментально невозможно установить термодинамическую активность отдельного сорта ионов.
При выборе способа оценки термодинамической активности всего электролита и активностей отдельных видов ионов можно исходить из следующих соображений.
Пусть имеется электролит типа CatxAnz, диссоциирующий по схеме:
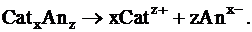
Химические потенциалы отдельных видов ионов можно выразить так:
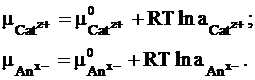
Так как химический потенциал электролита в целом определяется выражением
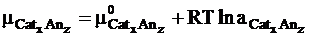
и в тоже время он равен сумме химических потенциалов составляющих его ионов
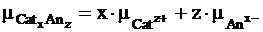 ,
,
то оказалось удобным ввести величину a±, называемую средней активностью электролита:
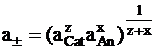 .
.
Подобным образом вводится средний коэффициент активности, средняя молярная доля, средняя молярность и средняя моляльность:
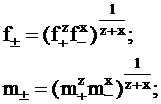 (4 - 4)
(4 - 4)
и т.д.
В частности, для бинарного электролита можно записать выражение для средней активности:
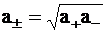 . (4 - 5)
. (4 - 5)
Для несимметричных электролитов в выражениях для средних величин появляются  числовые коэффициенты. Например, для электролита 1 - 2 этот коэффициент равен
числовые коэффициенты. Например, для электролита 1 - 2 этот коэффициент равен 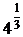 »1,587, для электролита типа 3 - 1 он равен
»1,587, для электролита типа 3 - 1 он равен 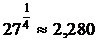 и т.д.
и т.д.
Экспериментально установлено, что коэффициент активности по мере разбавления раствора возрастает и в предельно разбавленных растворах стремится к единице.
Так как в предельно разбавленных растворах практически отсутствует взаимодействие между ионами, то коэффициент активности является поправкой на межионное взаимодействие в растворах, концентрация которых такова, что расстояние между ионами становится достаточным для возникновения взаимодействия.
Зависимость энергии взаимодействия между ионами от коэффициента активности можно установить следующим образом.
Предположим, что раствор электролита данной концентрации является идеальным и химический потенциал данного вида ионов может быть выражен уравнением:
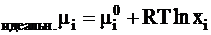 , (4 - 6)
, (4 - 6)
а химический потенциал этих же ионов в реальном растворе выразится так:
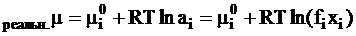 . (4 - 7)
. (4 - 7)
Отметим, что стандартное значение электрохимического потенциала 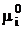 в обоих случаях одинаково. Поэтому можно записать:
в обоих случаях одинаково. Поэтому можно записать:
 . (4 - 8)
. (4 - 8)
Напомним, что химический потенциал представляет собой частную производную энергии Гиббса по числу молей данного вещества. Так как энергия Гиббса реального раствора отличается от энергии Гиббса идеального раствора на величину энергии межионного взаимодействия g, то зависимость коэффициента активности от энергии межионного взаимодействия приобретает следующий вид:
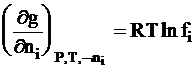 . (4 - 9)
. (4 - 9)
Как уже указывалось, энергию межионного взаимодействия можно рассчитать по теории Дебая - Хюккеля и по некоторым другим теориям. В частности, из уравнения (4 - 9) следует
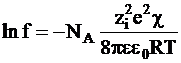 . (4 - 10)
. (4 - 10)
Так как толщина ионной атмосферы определяется по формуле:
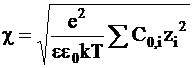 , (4 - 11)
, (4 - 11)
то коэффициент активности отдельного сорта ионов для достаточно разбавленных растворов можно вычислять по уравнению:
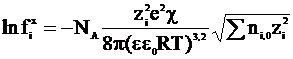 (4 - 12)
(4 - 12)
или, объединив постоянные формулы, можно воспользоваться выражением
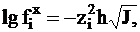 (4 - 13)
(4 - 13)
где J - ионная сила раствора, представляющая собой 1/2 суммы произведений концентраций ионов на квадрат их заряда, то есть
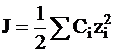 . (4 - 14)
. (4 - 14)
Средний коэффициент активности можно рассчитать по формуле:
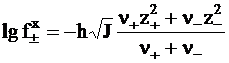 , (4 - 15)
, (4 - 15)
где n+ и n– - числа катионов и анионов, приходящихся на 1 молекулу электролита, z+ и z – - их заряды.
Для водного раствора 1,1-валентного электролита из теории Дебая - Хюккеля следует, что при 20° С h = 0,507.
