Электрические цепи с распределенными параметрами.

Электрические цепи с распределенными параметрами.

Основные понятия.

В принципе параметры любой электрической цепи (R, L, C, M, g) в той или иной мере распределены вдоль участков цепи. Соответственно токи и напряжения в такой цепи для одного и того же момента времени изменяются при переходе от одной точки цепи к соседней (в любой момент времени ток и напряжение в различных точках имеют различные значения).

В большинстве практических случаев с распределением параметров вдоль электрической цепи можно не считаться и в анализе цепей предполагать, что параметры цепи сосредоточены на ее участках.

Критерием применимости такого подхода является соотношение между скоростью изменения во времени напряжений и токов в цепи и скоростью распространения электромагнитной энергии вдоль электрической цепи.

Если это соотношение мало, то электрическую цепь рассматривают как цепь с сосредоточенными параметрами.

Если же эти скорости сравнимы, то электрическую цепь необходимо рассматривать как цепь с распределенными параметрами.

Примерами цепей с распределенными параметрами являются электрические линии с распределенными параметрами (длинные линии):

- линии передачи электрической энергии на большие расстояния;

- воздушные и кабельные линии телефонной и телеграфной связи;

- высокочастотные коаксиальные линии радиотехнических и телевизионных устройств.

Очевидно, что токи и напряжения в длинных линиях (линии с распределенными параметрами) являются функциями двух независимых переменных: времени t и координаты х, отсчитываемая как расстояние от рассматриваемой точки линии до ее начала (конца).

Соответственно процессы в длинных линиях описываются дифференциальными уравнениями в частных производных.

Если параметры линии распределены равномерно, то эта линия однородная (например, линия передачи электрической энергии, в которой сечение проводов, их взаимное расположение и характеристикой среды не изменяются по длине линии).

Если параметры линии не зависят от величины протекающих через линию токов, то это линия линейная.

Бегущие волны

Выражение для напряжения в любой точке линии (как и для тока) состоит из двух составляющих

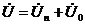или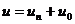

Итак,

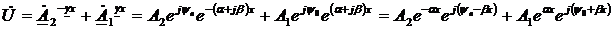
Для перехода от комплекса напряжения к функции времени необходимо умножить правые части формул на 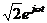и от произведений взять мнимую часть

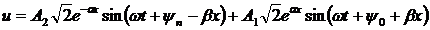
Первая составляющая представляет собой синусоиду, амплитуда которой по мере продвижения вдоль линии от ее начала (линии) уменьшается (затухает) по экспоненциальному закону ( 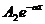), а аргумент этой синусоиды (фазы) является функцией времени и координаты.

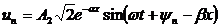
Иначе говоря, с одной стороны, в данной точке линии напряжение un является синусоидальной функцией времени (x=const, t=var).

С другой стороны, в данный момент времени напряжение un будет распределено вдоль линии также по синусоидальному закону.

В целом же, это даст перемещение вдоль линии неизменного фазового состояния напряжения (бегущей волны напряжения) от ее начала к концу с постоянной скоростью называемой фазовой скоростью Uф.

Аналогично образуется бегущая волна тока.

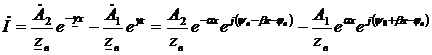
Откуда

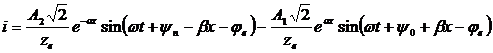
Электромагнитное состояние в любой точке линии определяется совокупностью электрического (волна напряжения) и магнитного (волна тока) полей.

Процесс перемещения электромагнитного состояния (электромагнитной волны) от источника энергии к приемнику, т. е. в нашем случае в сторону (направление) увеличения координаты х, от начала к концу линии называют падающей электромагнитной волной (прямая).

Уменьшение амплитуд падающих волн напряжения и тока по мере их продвижения вдоль линии объясняется наличием потерь в линии (х¹0).

Минимальное расстояние между двумя точками линии (имеющими одну и ту же фазу), фазы напряжения (тока) в которых отличаются на 2p, называется длина волны l.

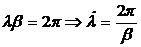
Фазовая скорость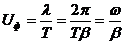

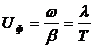
С другой стороны для линии без потерь в вакууме длина волны l равна расстоянию, на которое распространяется бегущая волна за период.

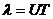, где U=300000 км/с.

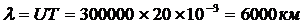
Вторая составляющая

представляет собой синусоиду, амплитуда которой возрастает по экспоненциальному закону при движении от ее начала или, иначе говоря, затухает по мере продвижения от конца к началу.

Процесс перемещения электромагнитного состояния (электромагнитной волны) от приемника к источнику энергии называется отраженной (обратной) электромагнитной волной.

Появление отраженных волн можно рассматривать как результат отражения падающих волн от конца линии.

Коэффициент отражения по напряжению qu – отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии.

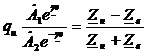
По току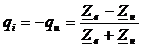

а) Если линия замкнута на конце на сопротивление, равное волновому ( 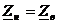), то qu=qi=0, т. е. в линии будут отсутствовать отраженные (обратные) волны. Это согласованный режим работы линии.

б) Если линия на конце разомкнута, т. е. 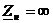, то qu=1 и qi=-1. Следовательно, на конце линии падающая и отраженная волны напряжения равны, в результате напряжение на конце линии в два раза больше падающей волны. Т. к. qi=-1, то результирующий ток равен 0.

в) Если линия закорочена на конце линии, т. е. 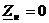, то qu=-1 и qi=1. В результате ток в конце линии равен удвоенному значению тока падающей волны, а напряжение равно 0.

Электрические цепи с распределенными параметрами.

Основные понятия.

В принципе параметры любой электрической цепи (R, L, C, M, g) в той или иной мере распределены вдоль участков цепи. Соответственно токи и напряжения в такой цепи для одного и того же момента времени изменяются при переходе от одной точки цепи к соседней (в любой момент времени ток и напряжение в различных точках имеют различные значения).

В большинстве практических случаев с распределением параметров вдоль электрической цепи можно не считаться и в анализе цепей предполагать, что параметры цепи сосредоточены на ее участках.

Критерием применимости такого подхода является соотношение между скоростью изменения во времени напряжений и токов в цепи и скоростью распространения электромагнитной энергии вдоль электрической цепи.

Если это соотношение мало, то электрическую цепь рассматривают как цепь с сосредоточенными параметрами.

Если же эти скорости сравнимы, то электрическую цепь необходимо рассматривать как цепь с распределенными параметрами.

Примерами цепей с распределенными параметрами являются электрические линии с распределенными параметрами (длинные линии):

- линии передачи электрической энергии на большие расстояния;

- воздушные и кабельные линии телефонной и телеграфной связи;

- высокочастотные коаксиальные линии радиотехнических и телевизионных устройств.

Очевидно, что токи и напряжения в длинных линиях (линии с распределенными параметрами) являются функциями двух независимых переменных: времени t и координаты х, отсчитываемая как расстояние от рассматриваемой точки линии до ее начала (конца).

Соответственно процессы в длинных линиях описываются дифференциальными уравнениями в частных производных.

Если параметры линии распределены равномерно, то эта линия однородная (например, линия передачи электрической энергии, в которой сечение проводов, их взаимное расположение и характеристикой среды не изменяются по длине линии).

Если параметры линии не зависят от величины протекающих через линию токов, то это линия линейная.