Частица в бесконечно глубокой потенциальной яме

Рассмотрим частицу, потенциальная энергия которой в интервале координат [0,l] равна нулю, а вне этого интервала бесконечно велика. Внутри такой потенциальной ямы стационарное уравнение Шредингера имеет вид такой же, как для свободной частицы (U=0):

-(ħ²/2m) 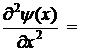E y(x) (9.4.4)

Ища решение (9.4.4) в виде осциллирующей функции 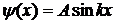, удовлетворяющей граничным условиям 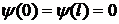, можно получить, что для частицы полная энергия квантована, то есть возможен только дискретный набор полных энергий:

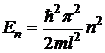, n=1, 2, 3, (9.4.5)

Целое число n, нумерующее допустимые значения полной энергии называется квантовым числом. Каждому квантовому состоянию с определенным значением полной энергии E_n соответствует своя волновая функция:

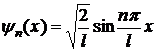(9.4.6)

Рис. 9.4.3

Первые четыре волновые функции, соответствующие уровням с n=1, 2, 3, 4, показаны на рис. 9.4.3.

Решенная выше простейшая задача отражает следующие общие свойства частицы, находящейся в потенциальной яме любой формы.

1) Частица, локализованная в потенциальной яме, может обладать только определенными дискретными значениями полной энергии E_n. Невозможно существование локализованных частиц с нулевой энергией. Состояние частицы с минимальной полной энергией называется основным состоянием.

2) Волновая функция частицы в состоянии с наименьшей полной энергией не обращается в ноль нигде в пределах потенциальной ямы. Волновые функции частицы во всех состояниях с бóльшими энергиями могут принимать нулевые значения в пределах ямы. Точки, где волновая функция обращается в ноль, называются узлами волновой функции. Количество узлов увеличивается на единицу при переходе к каждому следующему по энергии состоянию.

Теория атома

Атом водорода. Атомные спектры.

Первый постулат Бора - электроны могут двигаться вокруг атомного ядра, не излучая электромагнитную энергию, только по стационарным орбитам, определяемым из условия квантования момента импульса электрона:

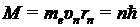, n = 1, 2, ... (9.5.1)

где m_е – масса электрона; υ_n – скорость электрона на n-й орбите; r_n – радиус n-й стационарной орбиты; n – номер стационарной орбиты; ħ − величина, связанная с постоянной Планка h соотношением ħ = h/ 2π, обычно также называемая постоянной Планка.

Второй постулат Бора - каждой разрешенной условием квантования электронной орбите соответствует определенное дискретное значение энергии. Переход с более удаленной от ядра орбиты на более близкую орбиту происходит скачкообразно и сопровождается испусканием кванта электромагнитного излучения.

Энергия испускаемого кванта Е, атакже его частота n,определяется из соотношения:

Е= Е_m - Е_n = hn, (9.5.2)

где Е_m - энергия электрона на орбите m; Е_n − энергия электрона на орбите n.

Из постулатов Бора следует, что полная энергия электрона на n-й орбите атома водорода Е_n может быть рассчитана по формуле:

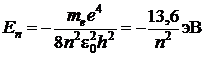, (9.5.3)

где n – номер стационарной орбиты, на которой находится электрон.

При переходе электрона с орбиты m, более удаленной от ядра, на более близкую к ядру орбиту n, согласно второму постулату Бора и выражению для полной энергии электрона на стационарной орбите, частота кванта излучения определяется соотношением:

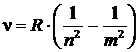. (9.5.4)

Это так называемая сериальная формула для спектра частот атома водорода, где R = 3,28984∙10¹⁵ Гц − постоянная величина, называемая постоянной Ридберга (полезно помнить, что hR = 13,6 эВ).

Теорию Бора можно успешно использовать не только для атома водорода, но и при рассмотрении водородоподобных атомов, т.е. ионов других химических элементов, состоящих из ядра с зарядом Ze и одного электрона (Не⁺, Li²⁺, Be³⁺, …), обладающих сходными оптическими свойствами. Так,сериальная формула для водородоподобных ионов имеет вид аналогичный сериальной формуле для водорода:

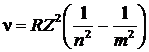, (9.5.5)

где Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода).

Теория атома Бора явилась промежуточным звеном в понимании новых квантовых закономерностей физики микромира. Принципы квантования электронных орбит, предложенные Бором в его теории атома, получили дальнейшее теоретическое обоснование в квантовой механике.