Векторное изображение электрических величин (тока, напряжения, ЭДС). Примечание комплексных чисел для расчета электрических цепей. Представление синусоидальных э.д.с., напряжений и токов

Комплексными числами

При изображении вращающихся векторов синусоидальных э.д.с, напряжения и тока на комплексной плоскости ось абсцисс плоскости декартовых координат совмещают с осью действительных или вещественных величин (ось + 1) комплексной плоскости. Тогда мгновенные значения синусоидальных величин получают на оси мнимых величин (ось+j) [18].

Как известно, каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в показательной, тригонометрической или алгебраической форме. Например, э.д.с. Emsm (cot + ц/с) изображенной на рисунке 9.1 вращающимся вектором, соответствует комплексное число.

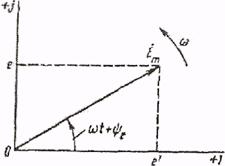
Рисунок 9.1 - Изображение синусоидальной э.д.с. вращающимся вектором на комплексной плоскости

Um=Um+jUm, (9.1)

Em ef(ωt+ψe)= Em cos(ωt+ψe)+jEmsi n+(ωt+ψe)= е'+je (9.2)

Фазовый уголь a>t+ у/, определяют по проекциям вектора на оси координат +1

tg (ωt+ψe)= е/е' (9.3)

Мнимая составляющая комплексного числа вектора на комплексной плоскости определяет синусоидальное изменение э.д.с. и обозначается символом Im

e=E_m sin(ωt+ψe)=Im E_m е'^(ωt+ψe). (9.4)

Комплексное число E ^{j(ωt+ψe )} удобно представить в виде произведения двух комплексных чисел

E_m е'^(ωt+ψe)= E_m е' ^ψe e ^ωt = E_m е^(ωt (9.5)

Первое комплексное число E_m соответствующее положению вектора в начальный момент времени, называют комплексной амплитудой

E_m = E_m е^tψe (9.6)

Второе комплексное число E^ψ является оператором поворота вектора на

угол cat относительно начального положения вектора.

Следовательно, мгновенное значение синусоидальной величины равно

мнимой части без знака j произведения комплекса амплитуды Ет и

оператора вращения

e=E_m sin(ωt+ψe)=Im E_m е^jωt. (9.7)

Переход от одной формы записи синусоидальных э.д.с, токов и

напряжений к другой осуществляется весьма просто с помощью формулы

Эйлера е^jωt - cos +/sin a.

Если, например, комплексная амплитуда напряжения задана в виде

комплексного числа в алгебраической форме

U_m =U_m+ jU_m (9.8) то, чтобы записать ее в показательной форме, необходимо найти начальную фазу <р „, т.е. угол, который образует вектор U_m с осью + 1.

В данном случае вектор U_m расположен в первом квадранте комплексной плоскости, и его начальная фаза (рисунок 9.2)определяется соотношением

Tg ψ_u=U_m /U_m (9.9)

Мгновенные значения напряжения

u=ImU_m e ^ωt =ImU_me'^(ωt+ψe)= U_m sin(ωt+ψe), (9.10)

Рассмотрим другой пример, когда комплексная амплитуда тока задана комплексным числом

I_m=-I_m+jI_m (9.11)

Вектор комплексной амплитуды тока /_т расположен во втором квадранте комплексной плоскости (рисунок 9.3). Начальная фаза этого тока

Ψ_t=180º-α (9.12)

Где tgψ_t=tg(180º-α)=- I_m/ I_m=tgα (9.13)

Если задано мгновенное значение тока в виде синусоиды / = I_msin(o)e + , то комплексную амплитуду записывают сначала показательной форме, а затем, по формуле Эйлера, переходят к алгебраической форме

I=Ie^iiψ (9.14)

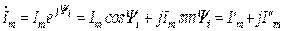(9.15)

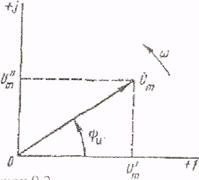
Рисунок 9.2 - начальная вектора комплексной амплитуды напряжения, расположенного в первом квадранте комплексной плоскости.

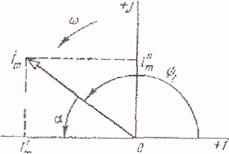
Рисунок 9.3 – первая начальная фаза вектора комплексной амплитуды тока, расположенного во втором квадранте комплексной плоскости

Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов. Например, для определения комплексной амплитуды результирующего тока (см. рисунок 9.4) достаточно сложить два комплексных числа, соответствующих комплексным амплитудам токов ветвей

I_3m= I_m +I_2m =I_3me^fψ3 (9.16)

Для определения комплексной амплитуды результирующей э.д.с. (см. рисунок 9.4) достаточно определить разность комплексных чисел, соответствующих комплексным амплитудам э.д.с. Е\_т и Е\_т.[18].