К р и о г е н н а я т е х н и к а

Кафедра криогенной техники

Лось В.И.

К р и о г е н н а я т е х н и к а

конспект лекций для студентов,

Обучающихся по специальности 8.090520

"Холодильные машины и установки"

Под редакцией профессора В.А. Наера

Одесса - 2002

Составитель – Лось Валерий Иосифович

доцент кафедры криогенной техники

Рецензент – Наер Вячеслав Андреевич

доктор технических наук, профессор,

заведующий кафедрой «Криогенная техника»

Конспект лекций по дисциплине «Криогенная техника» включает темы, связанные с особенностями поведения веществ при низких температурах, методами достижения низких температур, расчётом и анализом циклов криогенных установок, а также с теоретическими основами разделения смесей. Основная цель состояла в сжатом изложении основных направлений криогенной техники для студентов, специализирующихся в области умеренного холода, но желающих составить представление об этой области низкотемпературной техники.

В конспекте излагается третье начало термодинамики и рассматриваются особенности поведения тел вблизи абсолютного нуля. При изложении раздела, посвящённого методам достижения низких температур, использован материал, обобщённый и достаточно полно изложенный в учебнике Архарова А.М., Марфениной и Микулина Е.И «Криогенные системы». Разделы, связанные с рассмотрением циклов криогенных установок и теоретических основ разделения смесей, изложены таким образом, чтобы студент получил основное представление о методах сжижения и разделения газовых смесей. Для углублённого изучения, рассматриваемых в конспекте вопросов, приведен список соответствующей литературы.

Конспект лекций по дисциплине «Криогенная техника» для студентов специальности 8.090520 «Холодильные машины и установки» рассмотрен на заседании кафедры «Криогенная техника» (протокол № 2 от 10 октября 2002 года) и утверждён методической комиссией института низкотемпературной техники.

Председатель методической комиссии

доктор технических наук, профессор Е.С.Авдеев

о г л а в л е н и е

Введение.................................................................................................................................................................................... 3

1. ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ....................................................................................................................... 3

2. МЕТОДЫ ДОСТИЖЕНИЯ НИЗКИХ ТЕМПЕРАТУР.............................................................................................. 3

2.1. ПРОЦЕССЫ, СОПРОВОЖДАЮЩИЕСЯ ПОНИЖЕНИЕМ........................................................................... 3

ТЕМПЕРАТУРЫ В АДИАБАТНЫХ УСЛОВИЯХ..................................................................................................... 3

2.2. ИЗМЕНЕНИЕ ОСНОВНЫХ ТЕРМОДИНАМИЧЕСКИХ ВЕЛИЧИН ПРИ СЖАТИИ РЕАЛЬНОГО ГАЗА 3

2.3. ДРОССЕЛИРОВАНИЕ................................................................................................................................................. 3

2.4. ПРОЦЕСС U = CONST.................................................................................................................................................. 3

2.5. РАВНОВЕСНОЕ АДИАБАТНОЕ РАСШИРЕНИЕ ГАЗА................................................................................ 3

2.6. ВЫХЛОП ИЛИ СВОБОДНЫЙ ВЫПУСК ГАЗА ИЗ БАЛЛОНА............................................................ 3

ПРОЦЕСС ВПУСКА............................................................................................................................................................... 3

2.7. ПРОЦЕССЫ В АДИАБАТНОЙ СИСТЕМЕ С ПЕРЕМЕННОЙ МАCСОЙ................................................. 3

2.8. РАСШИРЕНИЕ ГАЗА В АДИАБАТНОЙ ВИХРЕВОЙ ТРУБЕ РАНКА—ХИЛША................................ 3

2.9. ПРОЦЕССЫ ВОЛНОВОГО РАСШИРЕНИЯ ГАЗА............................................................................................ 3

2.10. ОТКАЧКА ПАРОВ КИПЯЩЕЙ ЖИДКОСТИ.................................................................................................... 3

2.11. ПРОЦЕССЫ ОХЛАЖДЕНИЯ С ИСПОЛЬЗОВАНИЕМ РАБОЧЕЙ СРЕДЫ В ТВЕРДОМ СОСТОЯНИИ 3

2.12. ПРОЦЕССЫ ОХЛАЖДЕНИЯ, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ СВОЙСТВ ⁴He и ³He.. 3

2.13. РАЗЛИЧНЫЕ ПРОЦЕССЫ ОХЛАЖДЕНИЯ.................................................................................................... 3

3. ЦИКЛЫ КРИОГЕННЫХ УСТАНОВОК...................................................................................................................... 3

3.1. ЦИКЛ С ОДНОКРАТНЫМ ДРОССЕЛИРОВАНИЕМ....................................................................................... 3

3.2. ПОТЕРИ ХОЛОДА В ЦИКЛАХ КРИОГЕННЫХ УСТАНОВОК.................................................................. 3

3.3. ЦИКЛ С ОДНОКРАТНЫМ ДРОССЕЛИРОВАНИЕМ И.................................................................................. 3

ПРОМЕЖУТОЧНЫМ ОХЛАЖДЕНИЕМ..................................................................................................................... 3

3.4. ДЕТАНДЕРНЫЕ ЦИКЛЫ........................................................................................................................................... 3

3.5. ДЕТАНДЕРНЫЙ ЦИКЛ СРЕДНЕГО ДАВЛЕНИЯ............................................................................................ 3

3.6. ДЕТАНДЕРНЫЙ ЦИКЛ ВЫСОКОГО ДАВЛЕНИЯ.......................................................................................... 3

3.7. ДЕТАНДЕРНЫЙ ЦИКЛ НИЗКОГО ДАВЛЕНИЯ............................................................................................... 3

3.8. Газовые криогенные циклы....................................................................................................................... 3

4. Теоретические основы разделения смесей....................................................................................... 3

4.1. Термодинамические диаграммы смесей...................................................................................... 3

4.2. Теоретические основы процесса ректификации.................................................................. 3

4.3. Методы расчета процесса ректификации..................................................................................... 3

литература.............................................................................................................................................................................. 3

Введение

Криогенная техника – самая молодая отрасль холодильной техники. Развитие криогенной техники тесно связано с прогрессом новых отраслей промышленности. Интенсивное развитие криогенной техники в значительной степени обязано широкому использованию продуктов разделения воздуха, природного газа и различных газовых смесей в химической, металлургической и других отраслях промышленности.

В настоящее время в значительных масштабах используются температуры жидкого водорода ( 20,4 К). Всё большее значение приобретают температуры жидкого гелия ( 4,2 К) в практической радиотехнике, в радиоэлектронике.

Значительное количество воздухоразделительных и газоразделительных установок находится в эксплуатации. Установки такого рода отличаются большой энергоёмкостью. Поэтому серьёзное значение имеет использование методов анализа энергетической эффективности процессов и определения оптимальных режимов работы установок. Достаточное внимание в криогенной технике уделяется вопросам теплообмена и разделения, так как эти процессы, играя существенную роль в технике глубокого охлаждения, часто определяют конструктивное и аппаратурное решение всей установки.

Курс лекций содержит изложение термодинамических основ криогенной техники, достаточно подробное рассмотрение методов получения низких температур. Должное внимание уделяется расчёту и анализу теоретических и действительных циклов криогенных установок, анализу процессов разделения смесей. Основное внимание при этом уделено основному промышленному методу разделения смесей – ректификации. Изучение этого вопроса завершается рассмотрением методов расчёта числа теоретических тарелок.

ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ

Открытие третьего начала термодинамики связано с нахождением химического сродства—величины, характеризующей способность различных веществ химически реагировать другс другом. Эта величина определяется работой химических сил при реакции.

Первое и второе начала термодинамики позволяют вычислить химическое сродство только с точностью до некоторой неопределенной функции . Чтобы определить эту функцию, нужны в дополнение к обоим началам термодинамики новые опытные данные о свойствах тел. Поэтому Нернстом были предприняты широкие экспериментальные исследования поведения веществ при низкой температуре. В результате этих исследований и было сформулировано третье начало термодинамики:

по мере приближения температуры к 0 К энтропия всякой равновесной системы при изотермических процессах перестает зависеть от каких-либо термодинамических параметров состояния и в пределе (T =0 К) принимает одну и ту же для всех систем универсальную постоянную величину, которую можно принять равной нулю.

Общность этого утверждения состоит в том, что, во-первых, оно относится к любой равновесной системе и, во-вторых, что при Т 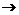0 К энтропия не зависит от значения любого параметра системы. Таким образом, по третьему началу,

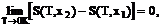(1.1 )

или

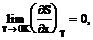(1.2 )

где х—любойтермодинамический параметр.

Предельное значение энтропии, поскольку оно одно и то же для всех систем, не имеет какого-либо физического смысла и поэтому полагается равным нулю. Как показывает статистическое рассмотрение этого вопроса, энтропия, по своему существу, определена с точностью до произвольной постоянной (подобно, например, электростатическому потенциалу системы зарядов в какой-либо точке поля). Таким образом, нет смысла вводить некую «абсолютную энтропию», как это делал Планк и некоторые другие ученые.

Постоянство энтропии (S 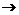0) при Т 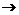0 К, согласно (1.1), означает, что изотермический процесс T=0 К является одновременно и изоэнтропийным, а следовательно, и адиабатным. Таким образом, по третьему началу нулевая изотерма совпадает с нулевой изоэнтропой и адиабатой.

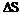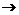Существует ряд веществ (некоторые сплавы, глицерин, СО, NO и др.), для которых при T 0 К стремится к отличной от нуля величине.

Как показал тщательный анализ, это кажущееся противоречие с третьим началом связано с «замораживанием» некоторых веществ в метастабильных или неравновесных состояниях, в которых при низкой температуре эти вещества могут находиться длительное время (несколько дней или недель), прежде чем придут в стабильные равновесные состояния. Когда измерения были проведены с большими промежутками времени, то оказалось, что разность энтропии 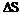во всех случаях исчезает при T 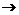0 К.

В настоящее время справедливость третьего начала обоснована для всех термодинамически равновесных систем.

Из третьего начала непосредственно следует недостижимость температуры 0 К.

Действительно, охлаждение системы осуществляется повторением следующих другза другом процессов адиабатного расширения (при котором понижается температура) и изотермического сжатия (при котором уменьшается энтропия). По третьему началу при изотермических процессах, когда температура приближается к 0 К, энтропия перестает изменяться при сжатии. Поэтому состояние с S=0 за конечное число указанных процессов недостижимо, а следовательно, недостижим и 0 К, так как согласно тому же началу состояние с T =0 К совпадает с состоянием S=0. К температуре 0 К можно лишь асимптотически приближаться.

Это следствие третьего начала по своему содержанию эквивалентно третьему началу, т. е. если третье начало неверно, то можно достичь температуры 0 К, и если можно достичь 0 К, то разность значений энтропии при 0 К должна быть отлична от нуля. По этой причине третьим началом термодинамики часто называют принцип недостижимости 0 К. Именно так сформулировал это начало Нернст, который не любил понятия энтропии и не употреблял его. Однако, формулировка третьего начала в виде закона о поведении энтропии при T 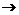0 К более удобна, так как непосредственно приводит к лаконичной математической записи , приведенной ранее.

Сказанное позволяет сформулировать следующее положение:

ДРОССЕЛИРОВАНИЕ

Адиабатное расширение газа в открытой системе в условиях стационарного течения без совершения внешней работы и прира­щения скорости на контрольной поверхности называется дроссели­рованием. Следует подчеркнуть, что стационарность течения пред­полагает в первую очередь постоянство давлений до и после дрос­селирования, а условие отсутствия приращения скорости течения на контрольной поверхности не исключает возможности ее мест­ного увеличения (или уменьшения) внутри системы, например, в самом дроссельном устройстве.

Для практического осуществления этого процесса на пути газа устанавливают какое-либо гидравлическое сопротивление: дрос­сельный вентиль, заслонку, калиброванное отверстие и пр.

Дж. Джоуль и У. Томсон исследовали этот процесс следующим образом . По медной трубке медленно протекал уста­новившийся поток газа (начальная температура T₁), проходя че­рез пробку, защищенную экранами. В опытах фиксировали изменения температуры при изменении перепада давле­ний Dр = p₁ — р_2.

Рассмот­рим элементарный объем мед­ленно текущего потока газа в двух сечениях, располо­женных по обе стороны от пробки и достаточно удален­ных от нее, где движение можно считать стационарным. Если скорости газа в рассматриваемых сечениях одинаковы, то для процесса дросселирования при l = 0 и q = 0 получим

i₂=i₁=const или u₁ + p₁v₁= u₂+ p₂v₂ = const. (2.2)

Так как никаких предположений о свойствах газов не делали, то полученный результат справедлив как для идеального, так и для реального газа: при дросселировании энтальпия газа не изменя­ется. Для идеального газа изменение внутренней энергии и эн­тальпии в любом процессе определяется выражениями du = c_v dT и di = c_p dT , откуда следует: если di = 0, то dT и du также равны нулю.

Для реального газа из уравнения (2.2) не следует постоянство температуры и внутренней энергии при дросселировании. При расширении реального газа увеличиваются расстояния между молекулами и совершается работа против молекулярных сил при­тяжения. Кроме того, в потоке реального газа работа гидродина­мических сил каждой единицы массы на входе и выходе из конт­рольной системы, равная произведению pv, различна из-за разной сжимаемости. Эти работы предопределяют изменение внутренней энергии и температуры, поэтому в общем случае для реального газа при дросселировании

di = 0 (i = const); dT ¹о; du ¹о . (2.3)

Таким образом, температура реального газа при дросселиро­вании может как понижаться, так и повышаться.

Процесс дросселирования необратим. Для идеального газа он необратим полностью, так как не сопровождается эффектами, ко­торые могли бы способствовать возвращению в исходное состояние. Приращение энтропии максимально и равно убыли энтропии при изотермическом сжатии идеального газа. Процесс дросселиро­вания реального газа частично обратим, так как сопровождается изменением температуры; при этом создается «тепловой резервуар» с температурой более высокой или более низкой и существует возможность использования перепада температур для получения работы (эту работу можно использовать для частичного возвращения газа в исходное состояние). Приращение энтропии при дросселирова­нии реального газа не равно изменению энтропии при его изо­термическом сжатии.

Определим изменение температуры реального газа при дрос­селировании

(¶Т /¶р)_i = a_i = (1/Ср) [Т (¶v/¶Т)р - v] (2.4)

Величина (¶Т/¶р)_i = a_i — дифференциальный эффект Джо­уля—Томсона, определяющий изменение температуры при беско­нечно малом падении давления в процессе дросселирования.

Практически при дросселировании всегда имеется конечная разность давлений, поэтому для такого процесса

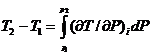(2.5)

Это выражение определяет так называемый интегральный эффект Джоуля—Томсона (изменение температуры при конечной разности давлений). Интегральный эффект дросселирования определяют обычно по таблицам или диаграммам (рис. 2.2).

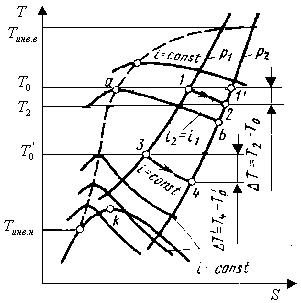Рис.2.2. Процесс дросселирования в диаграмме Т—s

Знак эффекта дроссели­рования может быть различным.

Если DТ/Dp = (T₂ — T₁)/(p₂ — p₁) > 0, то Т₂< T₁ (охлаждение), поскольку всегда p₂<p₁;

если DТ/Dр < 0, то Т₂> T₁, что соответствует нагреванию.

Из­менение знака дроссельного эффекта называют инверсией. В то­чке инверсии (¶T/¶p)_i=0. Кривая, на которой (¶T/¶p)_i=0 ,называется кривой инверсии.

Кривая инверсии разграни­чивает области положительного (охлаждение) и отрицательного (нагревание) дроссель-эффекта.

На рис. 2.3. приведены кривые инверсии для некоторых газов. Область под кривой инверсии соответствует положительному дрос­сельному эффекту.

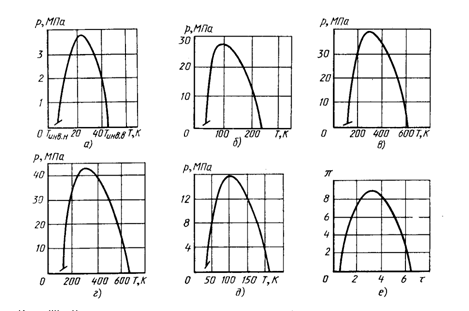
Рис. 2.3. Кривые инверсии для некоторых газов

а - гелия; б - неона; в - азота; г - воздуха; д - водорода; е - газа ван дер Ваальса

(в приведенных координатах)

Для каждого вещества сущест­вует максимальная температура инверсии Т_инв.в, выше которой при любых давлениях дроссель-эффект отрицателен. Эта темпе­ратура называется верхней температурой инверсии. Существует и так называемая нижняя температура инверсии Т_инв.н в обла­сти жидкости.

В координатах Т — s кривая инверсии проходит через экстремальные значения изоэнтальпии (i = const) и асимптотически приближается к Т_инв.в. как к тем­пературе инверсии малых давлений. Температуры инверсии для разных газов различны.

Для некоторых газов (воз­дух, азот, кислород) верхняя температура инверсии выше сред­ней температуры окружающей среды, для других (гелий, неон, водород) - ниже. Для охлаждения газа при дросселировании необходимо, прежде всего, понизить его темпера­туру до значения ниже верхней температуры инверсии Т_инв.в Если это условие выполнено, то возникает вопрос: до какого дав­ления p₁ следует сжать газ, чтобы достичь максимального инте­грального эффекта DT при известной начальной температуре T₀ (где То — обычно температура окружающей среды или тем­пература предварительного охлаждения). Продифференцировав выражение для интегрального дроссель-эффекта по

р и приравняв нулю полученное выражение, найдем

(¶Т / ¶р)_i. = 0. (2.6)

Это выражение является условием того, что искомая точка находится на кривой инверсии, а искомое давление равно давлению инверсии при данной температуре. Однако, в циклах с дросселированием практически (экономически) целесообразное давление сжатия может быть меньше давлений точки инверсии, например, в случае сжатия воздуха (при Т = 300 К ограничи­ваются давлением p » 20 МПа вместо 39 МПа). В гелиевых и водородных циклах с дросселированием оптимальные давления сжатия близки к давлениям инверсии.

При небольших давлениях значение a_i, для данного газа за­висит практически только от температуры. В области газообраз­ных состояний при снижении температуры дифференциальный эффект дрос­селирования возрастает.

При увеличении плотности газа a_i начинает зависеть от дав­ления. Экспериментально установлено, что a_i уменьшается при увеличении давления, а зависимость a_i от р близка к линейной. Влияние давления на a_i практически может сказываться только при сравнительно высоких давлениях .

Из изложенного ясно, что для увеличения интегрального эф­фекта начальную температуру процесса дросселирования следует понижать. Однако, надо четко понимать, что в низкотемпературных циклах с дросселированием холодопроизводительность теорети­ческого цикла без потерь холода не зависит от температуры начала дросселирования (процесс дросселирования в цикле не является холодопроизводящим). Увеличение интегрального эффекта дрос­селирования при снижении температуры открывает лишь прин­ципиальную возможность увеличения холодопроизводительности. Практически для этого необходимо так называемое предвари­тельное охлаждение. Роль предварительного охлаждения сво­дится к созданию теплового резервуара с температурой Т'_о, бо­лее низкой, чем температура окружающей среды T₀. При этом в области положительного дроссель-эффекта увеличивается раз­ность энтальпии сжатого и несжатого газов при одинаковой тем­пературе, что и обусловливает увеличение холодопроизводительности в цикле. Эту разность энтальпии, часто используемую при инженерных расчетах, обозначают в общем случае Di_T и называют изотермическим эффектом дросселирования. Зна­чение Di_T находят по таблицам или тепловым диаграммам как разность энтальпий сжатого и несжатого газов при данной тем­пературе.

Термины «тепловой» или «изотермический эффект дросселиро­вания» можно объяснить следующим образом. Если сравнить два состояния, соответствующие точкам 1 и 2 , то разность энтальпии i_1' – i₂, определяет количество теплоты, ко­торую можно отнять у тела, находящегося при температуре окру­жающей среды, используя эффект снижения температуры при дросселировании. С другой стороны, Di_T равна изменению энтальпии при изотермическом сжатии или расширении газа. Для того, чтобы в условиях стационарного течения расширить газ без совершения внешней работы и изменения температуры, т. е. изотермически, необходимо было бы подвести количество теплоты, равное Di_T0. При положительном дроссель эффекте Di_T опреде­ляет вклад компрессора в холодо-производительность цикла.

2.4. ПРОЦЕСС U = CONST

Если процесс расширения газа осуществить при тех же усло­виях, что и процесс дросселирования (без теплообмена с окру­жающими телами и без совершения внешней работы ), но в отличие от дросселирования расширять газ в закрытой системе, т. е. не в условиях стационарного течения, а в устройстве с жесткими стенками, то полная внутренняя энергия газа в такой системе будет постоянна. Это процесс расширения u= const; какого-либо характерного названия он не имеет. Схема реализации процесса u = const воспроизводит схему опыта Джоуля—Гей-Люссака (рис. 2.4).

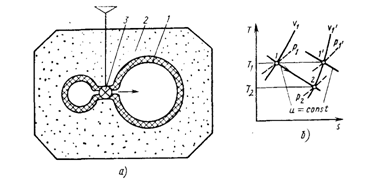
Рис.2.4. Схема реализации процесса u = const (а) и его изображение в диаграмме T—S (б)

Исследуемая система 1 состоит из двух сосудов с жест­кими стенками. Сосуды контактируют один с другим и изолиро­ваны от окружающей среды слоем изоляции 2. Начальные дав­ления газа в сосудах различные, а температуры газа одинаковые; начальное стационарное состояние с температурой T₁. При по­мощи вентиля 3 можно выравнивать давления газа в сосудах. При выпуске газа из одного сосуда давление и температура в нем снижаются; в это время в другом сосуде при втекании в него газа давление и температура повышаются. После выравнивания дав­лений в течение некоторого времени происходит выравнивание температур газа, пока система не придет в стационарное состояние с температурой Т₂. Изменение температуры газа в процессе u = const можно определить из уравнения

a_u = ( ¶T/ ¶p )_u=- (¶u / ¶р)_T / ( ¶u / ¶T )_p (2.7)

Для идеального газа ( ¶u / ¶v )_T= (¶u / ¶р)_T = 0, поэтому и dT = 0 в процессе u = const. Этот результат, установленный в опытах Джоуля—Гей-Люссака при расширении газов в области малых давлений еще в 1807 г., явился доказательством фунда­ментального положения о том, что внутренняя энергия идеального газа есть функция только температуры и не зависит от давления (плотности).

Однако, если этот опыт провести при расширении сильно сжа­тых газов, то температура не будет постоянной, а снизится: T₂< T₁. Таким об­разом, в процессе u = const для любого реального газа a_u — всегда положительная величина, т. е. температура снижается.

Процесс u = const не имеет столь большого практического значения, как процесс дросселирования i = const, однако, при­веденные соображения позволяют глубже понять сущность про­цессов внешне адиабатного расширения газа без совершения внеш­ней работы в условиях открытых и закрытых систем.

ПРОЦЕСС ВПУСКА

Рассмотрим процесс внешне адиабатного расширения газа при выпуске его из какой-либо емкости (баллона, цилиндра и пр.). Такой процесс часто называют выхлопом или свободным выпуском газа. Этот процесс — один из самых распространенных. Особенно часто его используют в низкотемпературных машинах как один из рабочих процессов циклов этих машин. Схема организации процесса выхлопа весьма проста. Баллон со сжатым газом имеет выпускной клапан, после открытия которого газ быстро вытекает из баллона и направляется в трубопровод .

Процесс выхлопа является нестационарным и неравновесным адиабатным процессом расширения газа с совершением внешней работы. Теплообмен газа со стенками исключен по условию, и не­равновесность обусловлена тем, что при изменении объема силы давления газа на контрольной поверхности системы не уравнове­шены силами противодавления. Начальные параметры газа в баллоне Т_н и p_H. Баллон герметично закрыт клапаном-задвижкой. После осво­бождения задвижка начинает двигаться без трения в выпу­скной трубе. Газ оказывает на задвижку давление, которое по­степенно падает. С другой стороны, на задвижку действует постоян­ная сила противодавления, так как газ вытекает в область по­стоянного давления p_k . Когда давление в баллоне достигнет р_k , задвижка остановится. Через некоторое время после окончания процесса в результате диффузии и смешения во всех частях системы установится рав­новесная температура T_k , кото­рую можно определить из выражения

T_H / T_k = k / [ 1+ (p_k /p_H) (k – 1)]. (2.13)

Снижение температуры газа при одинаковых T_H , p_H , p_k в неравновесном адиабатном процессе меньше, чем в изоэнтропном процессе. Следует обратить внимание на то, что при DP= (p_H - p_k ) ® dp соблюдаются условия квазиравновесия. В этом случае дифференциальные эффекты процесса выхлопа a_B и изоэнтропного процесса практически одинаковы:

a_B = (dT / dp)_B = a_SH = const. ( 2.14 )

Исходя из уравнение (2.14), нетрудно построить линии a_B = a_SH= const для процессов выхлопа в координатах Т — s при заданных T_H и p_H (рис. 2.6.).

Рис. 2.6. Линии процесса выхлопа в диаграмме T-s для воздуха

Из рисунка видно, в частности, что при использовании процесса выхлопа в качестве холодопроизводящего процесса нерациональны большие степени расширения в одной ступени. Чем меньше степень расширения, тем выше эффективность процесса выхлопа.

Если процесс выхлопа рассматривать во времени, то неизбежно приходится учитывать «температурное расслоение», или возник­новение температурного градиента в потоке выходящего из бал­лона газа.

Впервые процесс выхлопа был использован Л. Кальете в 1877 г. для ожижения кислорода и других газов. Затем он при­менен Э. Ольшевским и С. Вроблевским для получения ожиженных газов. В 1932 г. Ф. Симон успешно использовал этот процесс

для ожижения гелия. В 1959 г. У. Гиффорд и Мак-Магон по­строили оригинальный криогенератор, в котором циклически повторялся процесс выхлопа. Процесс свободного выпуска газа использован и в так называемой пульсационной трубе. Процесс выхлопа является одним из важней­ших рабочих процессов поршневых детандеров.

В заключение отметим, что обратным процессу выхлопа по физическому смыслу является процесс впуска газа в какую-либо емкость. В этом случае происходит неравновесное адиабатное сжатие газа, предварительно находившегося в баллоне. Если сжимаемый газ, находившийся в баллоне, остается изолирован­ным от входящих порций свежего газа, то можно записать, что

T_k / T_H = [ 1 + (k - 1) (p_k / p_H )] / k.(2.15)

При впуске газа с температурой T_Bx температуру T_k в бал­лоне после заполнения определяют с учетом смешения газа сжимаемого и вновь поступающего. Выполнив соответствующие вычисления, получим

T_k = (k T_Bx T_H p_k / p_H) / [T_H (p_k / p_H – 1) + k T_Bx. ] . (2.16)

Рассматривая процесс впуска во времени, необходимо также учитывать возникновение температурного градиента в потоке впускаемого газа. Температура в баллоне максимальна вдали от впускного клапана в зоне сжатия газа, находившегося перед впуском. Датчики температуры могут фиксировать кратковременно местное повышение температуры. Наиболее низкие тем­пературы в струях газа вблизи от входного окна или клапана. При интенсивном смешении температурный градиент исчезает, и в баллоне устанавливается температура, теоретически определя­емая уравнением (2.16). Неравномерное поле температур в со­суде, в который входит газ, можно в определенной конструкции стабилизировать во времени и, используя повышение температуры сжимаемого газа для передачи его энергии в окружающую среду, получить охлаждающее устройство. Это показано У. Гиффордом и Р. Лонгсвортом, осуществившими подобные процессы в пуль­сационной трубе .

ЦИКЛЫ КРИОГЕННЫХ УСТАНОВОК

В криогенной технике используют разнообразные циклы криогенных установок. Они

классифицируются по различным принципам. В соответствии с этим можно выделить

основные циклы криогенных установок:

1. Простые и сложные дроссельные циклы

2. Простые и сложные детандерные циклы

3. Комбинированные циклы

4. Газовые циклы

Для описания энергетических характеристик этих циклов пользуются различными величинами: холодопроизводительность, работа, холодильный коэффициент и коэффициент ожижения.

ЦИКЛ БЕЗ РЕГЕНЕРАЦИИ

Рассмотрим цикл с однократным дросселированием без регенерации, т.е. будем полагать, что дросселируется сжатый газ от температуры окружающей среды внутри кривой инверсии (при этом будет наблюдаться охлаждение). На рисунке 3.1 дано изображение рассматриваемого цикла: 1 – 2 - изотермическое сжатие; 2 – 3 - дросселирование; 3 – 1 –

изобарный нагрев. В действительности процесс 1 – 2 – это совокупность двух процессов: 1 – 2* - адиабатное сжатие и 2* - 2 – изобарное охлаждение. В реальных установках используется многоступенчатое сжатие с промежуточным охлаждением.

Для рассматриваемого цикла величина холодопроизводительности q₀ записывается в виде

q₀ = i₁ – i₂ =D i_T (3.1)

Холодопроизводительность цикла с однократным дросселированием без регенерации определяется величиной интегрального изотермического дроссель-эффекта.

Из рассмотрения цикла видно, что параметры лишь двух точек 1 и 2 определяют энергетические характеристики цикла. Точка 1 чаще всего определяется параметрами окружающей среды и поэтому является как бы фиксированной. Таким образом,фактически, лишь положением точки 2 определяются энергетические характеристики цикла. Положение точки 2, в свою очередь, определяется Т _окр.ср. и давлением Р₂. Следовательно, лишь одна величина -давление сжатия Р₂ влияет на энергетические характери

стики цикла .

Рис. 3.1. Цикл с однократным дросселирование без регенерации

При заданной температуре Т окр.ср. максимальное давление, при котором холодопроизводительность цикла будет максимальной, соответствует давлению инверсии Ринв., которое определяется изобарой, проходящей через точку касания изоэнтальпы и изотермы окружающей среды. Например, для воздуха при Т окр.ср. = 300 К значение Ринв. = 400 бар. На приводимом рисунке видно, что с ростом давления сжатия Р₂ холодопроизводительность цикла возрастает, если давление сжатия, разумеется, не превышает давления инверсии.

Таким образом, в рассматриваемом цикле холодопроизводительность растёт с ростом давления сжатия Р₂ до тех пор, пока оно не превышает давления инверсии Р_инв.

Для криогенных веществ, у которых максимальная температура инверсии меньше температуры окружающей среды (например, для гелия, неона, водорода) невозможно получить холод в цикле с однократным дросселированием, т.к. при дросселировании от температуры окружающей среды будет наблюдаться нагрев, а не охлаждение.

Если в качестве рабочего тела для этого цикла использовать идеальный газ, то холодопроизводительность q₀ = 0 ( точка 3 совпадает с точкой 1). Напомним, что для идеального газа a_i = 0, а следовательно, a_T = 0 и Di_T = 0.

Выражения для работы и холодильного коэффициента имеют вид

(3.2 )

Вместо точного выражения для работы, приведенного выше,часто используют приближенное выражение, полагая, что сжимаемый газ при температуре окружающей среды следует законам идеального газа

l = R T_окр.ср. ln (P₂/P₁) ( 3.3 )

Ошибка, возникающая при этом, например, для воздуха составляет около 10%, если

Р2 = 200 бар.

C ростом Р2 увеличивается холодопроизводительность q0 и работа цикла l. Вблизи кривой инверсии, однако, рост холодопроизводительности q0 замедляется . Работа цикла l c ростом Р2 увеличивается . Анализ показывает, что максимум холодильного коэффициента лежит при давлении более низком, чем давление, соответствующее максимуму холодопроизводительности. Рассмотрим влияние регенерации на энергетические характеристики цикла с однократным дросселированием.

ЦИКЛ С РЕГЕНЕРАЦИЕЙ

Рассмотрим цикл с однократным дросселированием и регенерацией (рис. 3.2). Этот цикл был первым криогенным циклом, который нашёл практическое применение в технике. Цикл с регенерацией (в виде отдельной ступени с дросселированием) является элементом большей части современных криогенных установок. Впервые цикл реализовали в 1895 г. независимо друг от друга Линде в Германии и Хэмпсон в Англии.

Рассмотрим контур, выделенный пунктиром, на рис. 3.2. Запишем энергетический баланс для выделенного контура

Рис. 3.2. Цикл с однократным дросселированием и регенерацией

1 – 2 – изотермическое сжатие; 2 – 3 – изобарное охлаждение прямого потока обратным;

3 – 4 – дросселирование; 4 – 5 – процесс подвода тепла (в рефрижераторных циклах);

5 – 1 – изобарный подогрев обратного потока.

(3.4)

Из полученного выражения следует, что и в цикле с регенерацией (как и в цикле без регенерации) холодопроизводительность цикла q0 определяется величиной интегрального изотермического дроссель-эффекта. Следовательно, включение регенеративного теплообменника, не изменив численно количество получаемого холода q0, понизило его температуру, т.е. сделало холод более ценным. Используя очевидное выражение для теплового баланса регенеративного теплообменника, можно привести и иную запись для холодопроизводительности цикла

(3.5)

Последнее выражение, где холодопроизводительность определяется положением точек 5 и 4 рассматри