Основное уравнение молекулярно-кинетической теории газов. Внутренняя энергия идеального газа
1. Основное уравнение молекулярно-кинетической теории идеальныхгазов
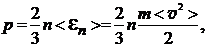
где n – концентрация молекул газа;<en> – средняя энергия поступательного движения одной молекулы;m – масса молекулы;<v2> – среднее значение квадрата скорости.
2. Средняя кинетическая энергия, приходящаяся на одну степень свободы
<e1>= 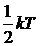 .
.
3. Средняя кинетическая энергия молекулы
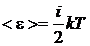 ,
,
где k = R/NА= 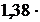 10-23 Дж/К – постоянная Больцмана;i – число степеней свободы молекулы.
10-23 Дж/К – постоянная Больцмана;i – число степеней свободы молекулы.
Для одноатомного газа i = 3; для двухатомного газа i = 5; для трёх и более атомных газовi = 6.
4. Внутренняя энергия произвольной массы идеального газа:
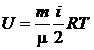 .
.
5. Зависимость давления газа от концентрации молекул и абсолютной температуры
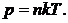
Примеры решения задач
Задача 1
Давление в сосуде с водородом равно 0,266 МПа. При этом средняя квадратичная скорость молекул равна 1400 м/с. Определить число молекул водорода в 1 см3.
| Дано: | Решение: |
V= 1 см3 = 10-6м3 р = 0,266 МПа 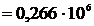 Па Па 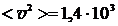 м/с м/с 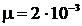 кг/моль кг/моль | Зависимость давления от концентрации n и абсолютной температуры Т имеет вид 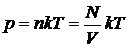 ,(1) отсюда число молекул N в данном объеме ,(1) отсюда число молекул N в данном объеме |
| N= ? |
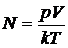 . (2)
. (2)
Неизвестную температуру Т определим, используя выражение для средней кинетической энергии поступательного движения молекулы
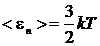 . (3)
. (3)
Приравняем 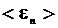 выражению для кинетической энергии молекулы
выражению для кинетической энергии молекулы
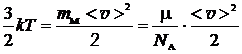 , (4)
, (4)
где масса молекулы водорода 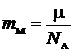 .
.
Из формулы (4) выразим Т:
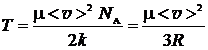 , (5)
, (5)
Подставив выражение (5) в формулу (2) и учитывая, что 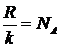 , получим:
, получим:
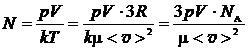 .
.
Проведем вычисления:
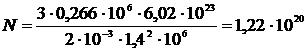 молекул.
молекул.
Задача 2
Кислород массой 1 кг находится при температуре 320 К. Определить 1) внутреннюю энергию газа; 2) среднюю кинетическую энергию вращательного движения молекул кислорода. Газ считать идеальным.
| Дано: | Решение: |
m= 1 кг Т = 320 К 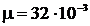 кг/моль кг/моль | Выражение для внутренней энергии идеального газа имеет вид 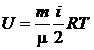 , (1) , (1) |
| 1) U= ? 2) <Eвр> = ? |
Кислород – двухатомный газ, для него полное число степеней свободы его молекул i = 5, из них 3 степени свободы приходятся на поступательное, а две – на вращательное движение
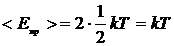 , (2)
, (2)
в данной массе газа содержится N молекул,
где
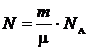 . (3)
. (3)
Средняя кинетическая энергия вращательного движения всех N молекул
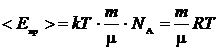 . (4)
. (4)
Проведем вычисления внутренней энергии по формуле (1), подставив в неё исходные данные:
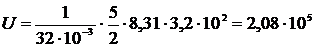 Дж = 208 кДж.
Дж = 208 кДж.
Проведем вычисление <Eвр> по формуле (4):
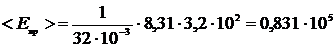 Дж = 83,1 кДж.
Дж = 83,1 кДж.
Элементы классической статистики
1. Скорости молекул:
- cредняя квадратичная
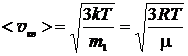 ,
,
- cредняя
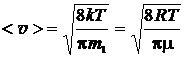 ,
,
- наиболее вероятная
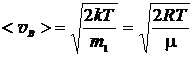 ,
,
где m1– масса молекулы, равная
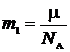 .
.
2. Средняя длина свободного пробега молекул газа
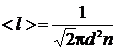 ,
,
где d – эффективный диаметр молекулы.
3. Среднее число соударений, испытываемых одной молекулой газа в единицу времени,
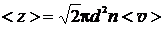 ,
,
где 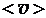 – средняя скорость молекул.
– средняя скорость молекул.
4. Барометрическая формула, выражающая зависимость давления идеального газа от высоты h над поверхностью Земли,
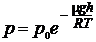
где p– давление газа на высоте h, p0– давление газа на высоте h = 0,Т– абсолютная температура воздуха на высоте h = 0.
Примеры решения задач
Задача 1
При температуре 300 К и некотором давлении средняя длина свободного пробега молекул кислорода равна 0,1 мкм. Чему равно среднее число столкновений, испытываемых молекулами в 1 с, если сосуд откачать до 0,1 первоначального давления? Температуру газа считать постоянной.
| Дано: | Решение: |
Т = 300 К <l> = 0,1 мкм = 10-7м 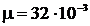 кг/моль кг/моль 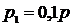 | Число столкновений молекул за 1 с можно определить по формуле 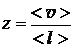 , (1) где , (1) где 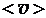 – средняя скорость молекул – средняя скорость молекул |
| <z1> ? |
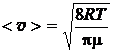 , (2)
, (2)
<l> – средняя длина свободного пробега.
Так как 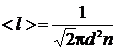 , а давление р = nkT, то длина свободного пробега молекул пропорциональна давлению.
, а давление р = nkT, то длина свободного пробега молекул пропорциональна давлению.
Тогда 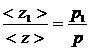 , т.е.
, т.е.
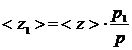 . (3)
. (3)
Подставив в формулу (3) выражение для <z>, получим:
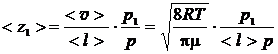 . (4)
. (4)
Проведем вычисления, подставив в формулу (4) числовые значения
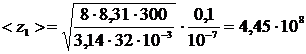 с-1.
с-1.
Задача 2
На сколько отличается атмосферное давление на вершине горы высотой 830 м от давления у подножия горы, если у подножия оно равно 100 кПа, а температура воздуха равна 290 К и не изменяется с высотой.
| Дано: | Решение: |
| h= 830 м р0= 100 кПа = 105 Па Т = 290 К | Зависимость давления газа от высоты выражается барометрической формулой 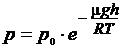 , (1) , (1) |
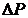 - ? - ? |
где р – атмосферное давление на вершине горы;р0 – давление у ее подножия; h – высота горы;Т – термодинамическая температура.
Находим искомое изменение давления
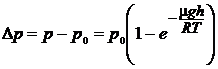 .
.
Воспользуемся разложением функции еxв ряд Тейлора и ограничимся первыми членами разложения, так как показатель экспоненты 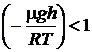 .
.
Получим:
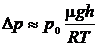 .
.
Произведем расчет, используя табличные данные:
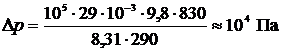 .
.
