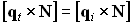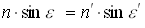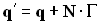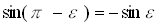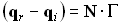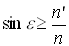Уравнение полоской и сферической волн

Отражение и преломление света на границе раздела двух сред

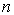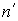Рассмотрим падение плоской волны на границу, разделяющую две прозрачные однородные диэлектрические среды с показателями преломления и . Будем считать, что граница представляет собой плоскость (так как в пределах бесконечно малой области любую поверхность можно считать плоской). Будем также считать, что сама граница раздела свет не поглощает.

После прохождения границы раздела двух сред падающая плоская волна (луч 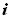) разделяется на две волны: проходящую во вторую среду (луч 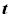) и отраженную (луч 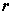) (рис.3.1.1).

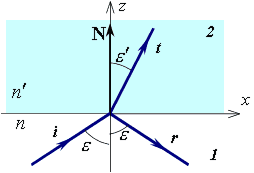
Рис.3.1.1. Преломление и отражение света на границе двух сред.

На рис.3.1.1 N – вектор нормали к поверхности в точке падения единичной длины 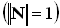. Поместим начало координат в точку падения. Определим следующие величины:

Угол падения 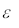– это угол между лучом 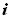, падающим на преломляющую или отражающую поверхность, и нормалью 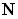к поверхности в точке падения.

Угол преломления 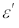– это угол между преломленным лучом 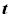и нормалью 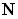к поверхности в точке преломления.

Угол отражения 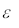– это угол между отраженным лучом 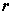и нормалью 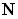к поверхности в точке отражения.

Закон преломления

После прохождения светом границы раздела двух сред необходимо определить направление распространения преломленной волны 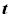и отраженной волны 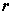, ираспределение энергии между отраженной и преломленной волной.

В соответствии с уравнением плоской волны (1.4.9) запишем выражения для комплексных амплитуд падающей, отраженной и преломленной волн:

уравнение падающей плоской волны

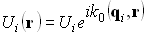(3.1.1)

уравнение преломленной плоской волны

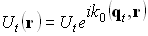(3.1.2)

уравнение отраженной плоской волны

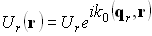(3.1.3)

где 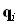, , 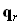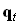– оптические векторы падающей, отраженной и преломленной волн, 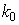– волновое число, 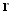– радиус-вектор произвольной точки.

Здесь мы используем соотношения скалярной теории, поскольку закон преломления одинаков для векторных и скалярных волн.

Из уравнений падающей и преломленной плоской волны следует, что на границе раздела двух сред у падающей и преломленной волн амплитуды могут быть различны, но должны совпадать значения эйконалов (этого требует условие физической реализуемости, так как иначе волна будет иметь разрыв на границе раздела):

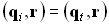(3.1.4)

Равенство (3.1.4) соблюдается на границе раздела, то есть для всех 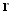, перпендикулярных вектору нормали. Таким образом, выражение (3.1.4) можно записать в виде:

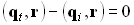при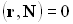

или:

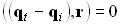при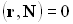

То есть 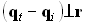, если 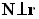. Выполнение этих условий возможно тогда и только тогда, когда 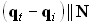. Таким образом, можно вывести формулировки закона преломления в векторной форме:

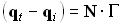(3.1.5)

где 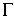– некоторый скаляр, или:

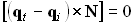(3.1.6)

или:

(3.1.7)

Так как длина оптического вектора равна показателю преломления среды ( 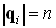, 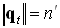), то из выражения (3.1.7) и определения векторного произведения можно вывести классический закон преломления Снеллиуса (Snell law).

Закон преломления (refraction law):

качественная часть закона:
падающий луч, преломленный луч и нормаль к поверхности раздела двух сред в точке падения лежат в одной плоскости.

количественная часть закона:
произведение показателя преломления на синус угла между лучом и нормалью сохраняет свое значение при переходе в следующую среду:

(3.1.8)

Чтобы найти скаляр 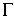, домножим скалярно выражение (3.1.5) на вектор нормали :

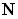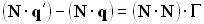
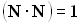, следовательно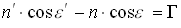

(3.1.9)

где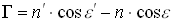

Величина 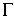имеет большое значение в математическом аппарате расчета лучей (ray tracing) на компьютере.

Закон отражения

Закон отражения можно вывести в векторной форме аналогично закону преломления, подставив вместо оптического вектора преломленного луча 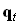оптический вектор отраженного луча 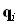(рис.3.1.2).

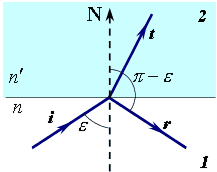
Рис.3.1.2. Отражение света на границе двух сред.

Закон отражения (reflection law):

(3.1.10)

Закон отражения можно вывести как частный случай закона преломления при 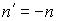(это просто прием для удобства расчета лучей вгеометрической оптике

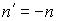, в отрицательном значении показателя преломления нет никакого физического смысла). Тогда случай отражения можно не выделять, а включать его в закон преломления при условии, что (рис.3.1.3).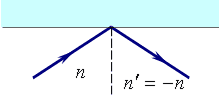

Рис.3.1.3. Отражение света на границе двух сред.

(3.1.11)

Величина 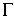в таком случае будет равна:

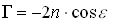(3.1.12)

Полное внутреннее отражение

Если угол падения 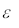невелик, то часть поля отражается, а часть преломляется. Однако, при переходе из более плотной среды в менее плотную 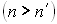, при некотором угле падения синус угла преломления по закону преломления должен быть больше единицы, что невозможно. Поэтому в таком случае преломления не происходит, а происходит полное внутреннее отражение (ПВО, entire inner reflection) (рис.3.1.4):

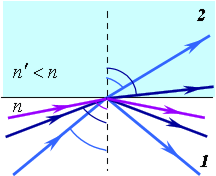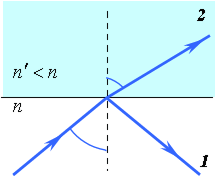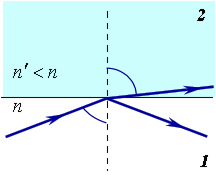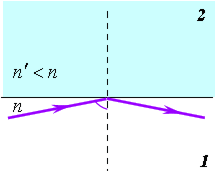
Рис.3.1.4. Полное внутреннее отражение.

Условие полного внутреннего отражения:

(3.1.13)

Явление ПВО широко используется в оптической технике благодаря тому, что при ПВО отражается 100% энергии, то есть потерь энергии нет. Таким образом, ПВО позволяет решить задачу полного отражения света: в зависимости от угла падения луч или почти полностью проходит, или почти полностью отражается.

Нарушенное полное внутреннее отражение (НПВО), которое возникает при оптическом контакте границы раздела со средой, используется в спектроскопии.

ПОЛНОЕ ВНУТРЕННЕЕ ОТРАЖЕНИЕ - отражение эл--магн. излучения (в частности, света) при его падении на границу двух прозрачных сред с показателями преломления 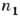и 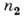из среды с большим показателем преломления ( 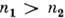) под углом 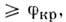для к-рого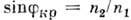 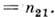Наим. угол падения 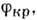при к-ром происходит П. в. о., наз. предельным (критическим) или углом полного отражения. Впервые П. в. о. описано И. Кеплером (J. Kepler) в 1600. Поток излучения, падающий при углах 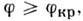испытывает полное отражение от границ раздела, целиком возвращается в среду с 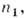т. о. коэф. отражения R = 1. В оптически менее плотной среде 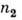в области вблизи границы существует конечное значение эл--магн. поля, однако поток энергии через границу отсутствует, т. к. перпендикулярная поверхности компонента Пойнтинга вектора ,усреднённая по времени, равна нулю. Это означает, что энергия проходит через границу дважды (входит и выходит обратно) и распространяется лишь вдоль поверхности среды в плоскости падения. Глубина проникновения излучения в среду 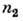определяется как расстояние, на к-ром амплитуда эл--магн. поля в оптически менее плотной среде убывает в 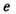раз.Эта глубина зависит от относит. показателя преломления 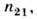длины волны 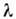p угла 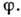Вблизи 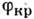глубина проникновения наибольшая, с ростом угла вплоть до 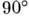плавно спадает до пост. значения.

Поле эл--магн. излучения в среде 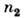существенно отличается от поля проходящей поперечной волны, т. к. в среде 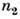компонента амплитуды электрич. вектора в направлении распространения волны не равна нулю. Все три компоненты х, у, zамплитуды волны имеют конечные значения при всех углах и в области 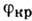могут значительно превышать 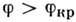по величине нач. значение амплитуды падающей волны (см. Нарушенное полное внутреннее отражение).

Схема распространения латеральной волны при полном внутреннем отражении вблизи критического угла пучка света с конечным поперечным сечением: 7 - падающий пучок; 2 - геометрически отражённый пучок; 3 - латеральная волна; Д - диафрагма.

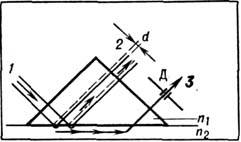
Процесс распространения эл--магн. излучения при П. в. о. в случае ограниченных пучков сопровождается продольным и поперечным смещением падающего пучка. Величина продольного смещения 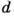зависит от состояния поляризации пучка, угла падения 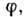величины 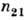и вблизи 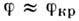равна

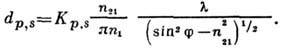
Для излучения, поляризованного в плоскости падения (р-полярнзация),для излучения, поляризованного перпендикулярно

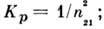
плоскости падения (s-поляризация), 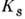= 1. Величина смещения пучка при П. в. о. коррелирует с глубиной проникновения эл--магн. излучения в оптически менее плотную среду 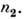Величина смещения 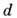сравнима с глубиной проникновения и по порядку величины близка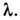

При П. в. о. p- и s-компоненты поляризованного излучения испытывают различный по величине сдвиг фаз, поэтому линейно поляризованное излучение после отражения становится эллиптически поляризованным. Разность фаз р- и s-компонент определяется из выражения

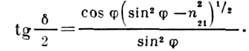
Величина 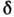имеет минимум в области углов 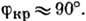Подбирая подходящий угол падения и значение 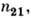можно получить сдвиг фаз, равный 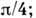для двух отражений величина сдвига удваивается. Такой приём используется в поляризац. устройствах (призма - ромб Френеля, см. Поляризационные приборы)для преобразования линейно поляризованного излучения в круговое.

Вследствие дифракции, обусловленной конечными размерами падающего пучка, при П. в. о. наряду с рассмотренным продольным смещением пучка наблюдается латеральная ("побочная") волна, распространяющаяся вдоль поверхности, к-рая играет роль своеобразного волновода (рис.). Латеральная волна возникает при угле, превышающем f_кr всего на 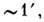и распространяется на расстояние, на неск. порядков превышающее величину продольного смещения регулярной волны, имеющей интенсивность, близкую к единице. Интенсивност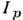и и 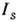пучков отражённой латеральной волны для р- и s-поляризованного излучения уменьшаются вдоль поверхности пропорционально кубу расстояния, на к-рое произошло смещение волны, и относятся между собой как 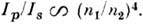В опыте с гелиево-кад-миевым лазером для границы вода - воздух латеральная волна регистрировалась на расстоянии до 7 см. Для расстояния 3 см и 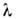= 441,6 нм интенсивность волны составляла 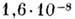от мощности падающего пучка света.

В отличие от селективного отражения металлов, к-рое может быть весьма высоким (но всегда коэф. отражения R < 1), при П. в. о. для прозрачных сред R = 1 для всех 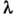и не зависит практически от числа отражений. Следует, однако, отметить, что отражение от механически полированной поверхности из-за рассеяния в поверхностном слое чуть меньше единицы на величину 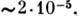Потери на рассеяние при П. в. о. от более совершенных границ раздела, напр. в волоконных световодах, ещё на неск. порядков меньше. Высокая отражат. способность границы в условиях П. в. о. широко используется в интегральной оптике, оптич. линиях связи, световодах и оптич. призмах. Высокая крутизна коэф. отражения вблизи f_кр лежит в основе измерит. устройств, предназначенных для определения показателя преломления (см. Рефрактометр ).Особенности конфигурации эл--магн. поля в условиях П. в. о., а также свойства латеральной волны используются в физике твёрдого тела для исследования поверхностных возбуждённых колебаний (плаз-монов, поляритонов), находят широкое применение в спектроскопич. методах контроля поверхности на основе нарушенного П. в. о., комбинационного рассеяния света, люминесценции и для обнаружения весьма низких значений концентраций молекул и величин поглощения, вплоть до значений безразмерного показателя поглощения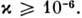

Формула тонкой линзы

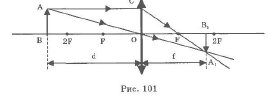
Формула тонкой линзы связывает d (расстояние от предмета до оптического центра линзы), f (расстояние от оптического центра до изображения) с фокусным расстоянием F (рис. 101).

Треугольник АВО подобен треугольнику OB₁A₁. Из подобия следует, что

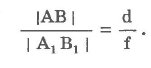
Треугольник OCF подобен треугольнику FB₁A₁. Из подобия следует, что

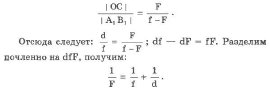
Это и есть формула тонкой линзы.

Расстояния F, d и f от линзы до действительных точек берутся со знаком плюс, расстояния от линзы до мнимых точек - со знаком минус.

Отношение размера изображения Н к линейному размеру предмета h называют линейным увеличением линзы Г.

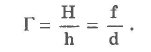
Тонкие линзы

Монохроматические волны

Монохроматическая волна - это строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.

Амплитуда и фаза такой волны могут изменяться от одной точки пространства к другой, частота же остается постоянной во всем пространстве.

Монохроматические волны не ограничены ни во времени, ни в пространстве, т.е. не имеют ни начала, ни конца. Поэтому они не могут быть реализованы в действительности. Однако эти идеализации играют громадную роль в учении о волнах и мы будем ими пользоваться.

Уравнение полоской и сферической волн

Волновые процессы представляют собой общий класс явлений.
Несмотря на бесконечное разнообразие физических процессов, вызывающих волны, образование волн происходит по одному общему типу. Возмущение, происшедшее в какой-нибудь точке в известный момент времени, проявляется спустя некоторое время на некотором расстоянии от начальной точки, т. е. передается с определенной скоростью. Рассмотрим самый простой пространственно одномерный случай: распространение возмущения вдоль оси ОХ. Тогда можно изобразить возмущение f как функцию координаты x и времени t, 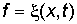. Распространение возмущения со скоростью u вдоль направления ОХ изобразится той же функцией, в аргумент которой t и x входят в комбинаци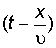и или 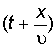в зависимости от направления распространения возмущения вдоль оси ОХ.

В этом случае волновое уравнение (2.5) имеет вид:

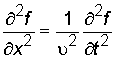, (2.6)

а его общее решение выглядит

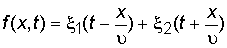. (2.7)

Если в начальный момент времени t = 0 графически изобразить функции x₁(x) и x₂(x), то в последующие моменты времени эти функции будут смещаться вдоль оси ОХ со скоростью u как целое: x₁ – вправо, x₂ – влево.

Рассмотрим гармонические монохроматические волны, т. е. синусоидальные волны с одной циклической частотой w = 2pn.

В этом случае зависимость любой величины f от времени t в общем виде выглядит так:

,

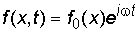где f₀ – значение рассматриваемой величины в точке с координатой x в начальный момент времени t = 0. Решение волнового уравнения (2.6), удовлетворяющее условию (2.7) и дающее гармоническую зависимость f от t, имеет вид:

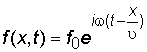. (2.8)

Выражением 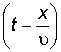в формуле (2.8) определяется фаза волны (ее состояние в данный момент времени в данной точке пространства). В данный момент времени волновой фронт – геометрическое место точек, в которых фаза колебаний имеет одно и то же значение – описывается уравнением x = const. Это плоскость, нормальная к оси OX и перпендикулярная направлению распространения волны. Таким образом, волновой фронт распространяется вправо с фазовой скоростью u. Так как волновой фронт является плоскостью, мы получили плоскую волну. Нам необходимо также выражение для плоской волны, распространяющейся в произвольном направлении, характеризуемом постоянным единичным вектором 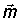. Так как уравнение плоскости, перпендикулярной вектору 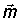, имеет вид
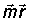= const, уравнение плоской волны можно записать в виде:

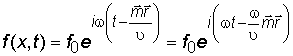. (2.9)

Электромагнитные волныпредставляют собой распространение электромагнитных полей в пространстве и времени.

Деление электромагнитного поля на электрическое и магнитное зависит от выбора системы отсчета. Действительно, вокруг зарядов, покоящихся в одной системе отсчета, существует только электрическое поле; однако эти же заряды будут двигаться относительно другой системы отсчета и порождать в этой системе отсчета, кроме электрического, еще и магнитное поле. Таким образом, теория Максвелла связала воедино электрические и магнитные явления.

- всякое изменение электрического поля возбуждает в окружающем пространстве вихревое магнитное поле, линии индукции которого расположены в плоскости, перпендикулярной линиям напряженности переменного электрического поля, и охватывают их (рис.2б).Линии индукции возникающего магнитного поля образуют с вектором «правый винт». Такие волны могут распространяться не только в газах, жидкостях и твердых средах, но и в вакууме.Скорость электромагнитных волн в вакууме с=300000 км/с. Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.Распространение электромагнитной волны в диэлектрике представляет собой непрерывное поглощение и переизлучение электромагнитной энергии электронами и ионами вещества, совершающими вынужденные колебания в переменном электрическом поле волны. При этом в диэлектрикепроисходит уменьшение скорости волны.Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 4), ориентированную перпендикулярно направлению распространения волны, то за малое время Дt через площадку протечет энергия ДWэм, равная

ДWэм = (wэ + wм)хSДt.

При переходе из одной среды в другую частота волны не изменяется.Электромагнитные волны могут поглощаться веществом. Это обусловлено резонансным поглощением энергии заряженными частицами вещества. Если собственная частота колебаний частиц диэлектрика сильно отличается от частоты электромагнитной волны, поглощение происходит слабо, и среда становится прозрачной для электромагнитной волны.Попадая на границу раздела двух сред, часть волны отражается, а часть проходит в другую среду,преломляясь. Если второй средой является металл, то прошедшая во вторую среду волна быстро затухает, а большая часть энергии (особенно у низкочастотных колебаний) отражается в первую среду (металлы являются непрозрачными для электромагнитных волн).Распространяясь в средах, электромагнитные волны, как и всякие другие волны, могут испытывать преломление и отражение на границе раздела сред, дисперсию, поглощение, интерференцию; при распространении в неоднородных средах наблюдаются дифракция волн, рассеяние волн и другие явления.Из теории Максвелла следует, что электромагнитные волны должны оказывать давление на поглощающее или отражающее тело. Давление электромагнитного излучения объясняется тем, что под действием электрического поля волны в веществе возникают слабые токи, то есть упорядоченное движение заряженных частиц. На эти токи действует сила Ампера со стороны магнитного поля волны, направленная в толщу вещества. Эта сила и создает результирующее давление. Обычно давление электромагнитного излучения ничтожно мало. Так, например, давление солнечного излучения, приходящего на Землю, на абсолютно поглощающую поверхность составляет примерно 5 мкПа.