Изучение явления дифракции и определение длины волны света при помощи дифракционной решетки

Цель работы: изучить явление дифракции; экспериментально определить границы видимой части спектра.

Приборы и принадлежности: оптическая скамья, дифракционные решетки, источник света, щелевая диафрагма, светофильтры и измерительная линейка.

Введение

Дифракцией называется явление огибания волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Так, например, если свет от источника S (рис. 1) направить на непрозрачный экран А с круглым отверстием а, сравнимым с длиной волны λ, то на экране В вокруг светлого пятна наблюдаются размытые кольца в области геометрической тени, показанные пунктирными окружностями.

Дифракция объясняется на основе волновой теории света и принципа Гюйгенса. Часть поверхности волны, дошедшей до экрана А, проходит в отверстие а.

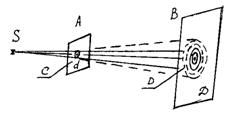
Рисунок 1

Согласно принципу Гюйгенса каждая точка волновой поверхности излучает вторичные элементарные волны, распространяющиеся от отверстия во всем полупространстве справа от экрана А. Дойдя до экрана В, они создают освещенность его за пределами светлого пятна, интенсивность которой убывает с удалением от него, причем неравномерно, образуя размытые светлые кольца. Образование этих колец обусловлено интерференцией света и объясняется с помощью зон Френеля.

Метод зон Френеля лежит в основе изучения большинства дифракционных явлений и заключается в следующем. Пусть в точке S (рис. 2) помещен точечный источник света, а в точке Р находится наблюдатель. Фронт волны через некоторое время Δt займет положение АОВ и пересечет оптическую ось в точке C.

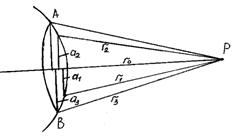
Рисунок 2

Радиусом r₀ из точки Р описываем сферическую поверхность, которая касается поверхности АОВ в точке C. Далее радиусом, увеличивающимся на λ/2, т.е. и т.д. описываем еще ряд сферических поверхностей, которые вырежут из поверхности АОВ ряд колец с радиусами а₁, а₂, а₃... и т. д. Первое кольцо называется 1-й зоной Френеля, а 2-е, 3-е и т. д. зоны Френеля будут кольцами. Каждая зона излучает свет, а так как расстояния до соседних зон отличаются друг от друга на λ/2, то в точку Р от соседних зон будут приходить лучи с разностью хода λ/2, т. е. в противоположных фазах, а при равных амплитудах будут компенсировать друг друга. Но амплитуды лучей, пришедших в точку Р, будут тем меньше, чем больше номер зоны, т. е. чем дальше расположена зона от точки Р. В теоретическом курсе доказывается, что результирующая амплитуда лучей А_р, пришедших от всех зон, если число зон стремится к бесконечности, оказывается равной половине амплитуды волны, пришедшей от 1-й зоны, или. целой амплитуде лучей, пришедших от половины этой зоны, т. е.

А_p=A₁/2 (1)

где А_Р - результирующая амплитуда колебаний в точке Р,

а₁ - амплитуда волны, пришедшей от 1-й зоны в точку Р. Источник S из точки Р будет виден в направлении прямойРОS. Следовательно, явление дифракции не противоречит закону прямолинейного распространения света.

Применим рассмотренный метод зон Френеля для объяснения светлых колец, образующихся на экране В (рис. 1). Для этого из точки Р, расположенной в центре светлого пятна D на экране В необходимо описать ряд сферических поверхностей и посчитать, сколько зон Френеля укладывается на ширине отверстия “а”. Так как “а” мало, то на нем вмещается небольшое число зон. Будем считать амплитуды волн от различных зон, пришедших в точку Р, одинаковыми. Вследствие того, что расстояние до соседних зон отличается на λ/2, лучи в точку Р попадут с разностью хода λ/2 и при сложении полностью погасят друг друга. Отсюда вытекает правило: в точке наблюдения Р лучи будут усиливать друг друга, если на ширине отверстия укладывается нечетное число зон Френеля, и ослаблять — если четное число зон.

А так как число зон на ширине отверстия “а” зависит от положения точки наблюдения Р относительно точки S, то на экране будет наблюдаться либо усиление, либо ослабление интенсивности света. Весь экран покрывается чередующимися светлыми и темными кольцами ослабевающей интенсивности при удалении от центра пятна. В центре пятна Р тоже наблюдается чередование усиления и ослабления интенсивности вследствие, того, что при приближении экрана В к источнику S число зон, укладывающихся на ширине отверстия, увеличивается, а при удалении — уменьшается.

Аналогичная дифракционная картина наблюдается также и в том случае, если вместо круглого отверстия диаметром “а”, в экране будет прорезана узкая щель шириной “а”. Кроме светлой полосы, расположенной в центре картины, ееназывают максимумом нулевого порядка, представляющей собой изображение щели, получаются светлые полосы первого, второго и т. д. порядка, расположенные по обе стороны от полосы нулевого порядка (см. рис. 3).

Чтобы рассмотреть образование этих полос, допустим, что в экране А прорезаны две щели шириной а, между которыми расположена непрозрачная полоса экрана шириной b (рис. 3). На щели падает плоская волна, ограниченная лучами 1 и 2. В теоретическом курсе доказывается, что указанные две щели можно рассматривать как два когерентных источника, каждый из которых создает свою дифракционную картину; наложение их друг на друга создает результирующую картину. Для ее наблюдения необходимо поставить линзу и сфокусировать лучи от обеих щелей на экране.

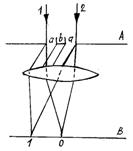
Рисунок 3

Четкую дифракционную картину можно получить при использовании дифракционной решетки, которая представляет собой прозрачную пластину с параллельными бороздками, прорезанными резцами специальной делительной машины. Бороздка отражает, рассеивает падающий на нее свет и выполняет роль темного промежутка между участками прозрачных поверхностей, которые хорошо пропускают свет и служат щелями решетки. В теоретическом курсе доказывается, что каждая из щелей решетки создает дифракционную картину. Эти картины накладываются друг на друга так, что на экране В максимумы каждой щели усиливаются, а минимумы ослабляются. В результате образуется четкая дифракционная картина, состоящая из ярких узких полос, разделенных широкими темными полосами (рис. 4).

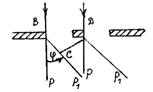
Рисунок 4 Рисунок 5

Рассмотрим пучок света, падающий на решетку перпендикулярно ее плоскости (см. рис. 5). Кроме лучей, проходящих без отклонения, за решеткой будут лучи, отклоненные на различные углы.

Выберем из всех отклоненных лучей только те лучи, которые отклонились на угол у от первоначального направления. До точки наблюдения эти лучи проходят разные пути, различающиеся на длину ВС. Если в этой разности хода укладывается четное число полуволн, то эти лучи усиливают друг друга, а если нечетное -то лучи ослабляют друг друга.

Отсюда следует записать простые соотношения для ΔВСД:

Усиление 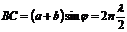(2)

Ослабление (3)

Если обозначить а + в = d, d называют постоянной решетки, то из уравнений (2) и (3) получаются условия главных максимумов и главных минимумов для решетки

max 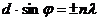(4)

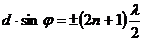min (5)

Здесь знаки ± означают, что максимумы и минимумы располагаются по обе стороны от центрального (справа и слева).

Если решетку освещать белым светом, то максимумы будут окрашенными. Белый свет вследствие дифракции волн будет разлагаться в спектр. Причем, ближе к центральному (нулевому) максимуму будут расположены максимумы для фиолетовых лучей, а дальше от него — для зеленых, желтых, красных.

Уравнение (4) можно записать 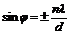(4.6)

Оно показывает, что угол дифракции лучей зависит от длины волны этих лучей. Число n называют порядком спектра. Чем больше n, тем слабее будет дифракционный максимум, n может принимать значения 0, 1, 2, 3...

В данной работе необходимо определить границы видимой части спектра, т. е. найти длины волн красного и фиолетового цветов. Из уравнения (4.4) получаем уравнение для определения длины волны света λ. 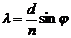(7)

d — постоянная решетки.Она дается на приборе.

N— порядок спектра. Вы берете его сами. Лучше наблюдать первый порядок, т. Е. ближайший за центральным.

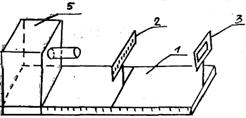
Рисунок 6

Схема установки показана на рис. 6. На оптической скамье 1 установили источник света S (электрическая лампа в кожухе с конденсором, позволяющим получать параллельный пучок лучей), непрозрачный экран 2 с узкой щелью и делениями и дифракционная решетка 3.

Пучок лучей, пройдя через щель в экране 2 попадает на дифракционную решетку. Глядя на экран через дифракционную решетку, видим яркую белую щель, по обе стороны от которой располагаются спектры. Ближайший к щели спектр является первым, далее второй и т. д. 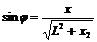(8)

Здесь L — расстояние от экрана 2 до решетки 3;

x — расстояние от щели до соответствующего максимума n-го порядка с длиной волны λ.

Но так как x<<L, то 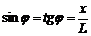(9)

Подставив в уравнение (7) значение синуса φ из уравнения (9), получим

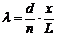(10)

Порядок выполнения работы

1. Включите источник света.

2. Получите спектры при рассматривании щели на экране 2 через дифракционную решетку 3.

3. Измерьте расстояния от щели до экрана, от щели до красной и фиолетовой линий в спектрах первого порядка.

4. Данные занесите в заранее заготовленную таблицу.

5. Для каждого цвета по уравнению (10) определите длину волны.

6. Определите погрешности измерений.

Таблица 1

№п/п	цвет	L, мм	Х, мм	λ, мм	Δλ, мм	Еλ, %	n
слева	справа	среднее
	Красный
	Фиолетов.

Контрольные вопросы

1. Объясните явление дифракции света.

2. Сформулируйте принцип Гюйгенса—Френеля.

3. В каких условиях наблюдаются дифракционные явления?

4. В чем заключается метод зон Френеля?

5. Условия получения максимума дифракции от решетки и щели.

6. Что называется дифракционным спектром? Чем он отличается от призматического или дисперсионного?

7. Как и почему располагаются цветные линии в дифракционном спектре?

ЛАБОРАТОРНАЯ РАБОТА №23