Ускорение точки при прямолинейном движении
Если вектор 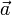 = const, т.е. не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
= const, т.е. не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
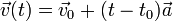
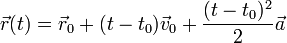 .
.
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть 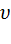 2 >
2 > 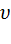 1, а направление вектора ускорения совпадает с вектором скорости
1, а направление вектора ускорения совпадает с вектором скорости 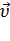 2, (т.е. а < 0).
2, (т.е. а < 0).
Если скорость тела по модулю уменьшается, то есть 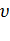 2 <
2 < 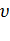 1, то направление вектора ускорения противоположно направлению вектора скорости
1, то направление вектора ускорения противоположно направлению вектора скорости 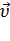 2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 13 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
2. Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 13 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рис. 13.
Ускорение точки при криволинейном движении
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих.
Действительно, при движении тела по криволинейной траектории его скорость  изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости  за некоторый малый промежуток времени Δt можно задать с помощью вектора ∆
за некоторый малый промежуток времени Δt можно задать с помощью вектора ∆ 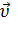 (рис. 14).
(рис. 14).
Вектор изменения скорости ∆ 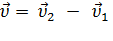 за малое время Δt можно разложить на две составляющие:
за малое время Δt можно разложить на две составляющие: 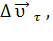 направленную вдоль вектора
направленную вдоль вектора 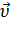 (касательная составляющая), и
(касательная составляющая), и 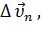 направленную перпендикулярно вектору
направленную перпендикулярно вектору  (нормальная составляющая).
(нормальная составляющая).
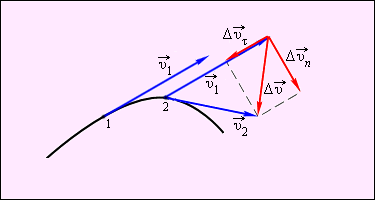
Рис. 14. Изменение вектора скорости по величине и направлению. ∆  = = 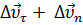 – изменение вектора скорости за время ∆t. – изменение вектора скорости за время ∆t. |
Тогда мгновенное ускорение равно:  =
= 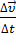 =
= 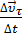 +
+ 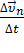 , (∆t
, (∆t  0).
0).
Направление вектора ускорения 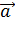 в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости 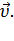 Составляющие вектора ускорения
Составляющие вектора ускорения  называют касательным (тангенциальным)
называют касательным (тангенциальным) 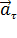 и нормальным
и нормальным 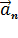 ускорениями (рис. 15).
ускорениями (рис. 15).
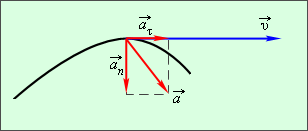
Рис. 15.
Касательное и нормальное ускорения.
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении:
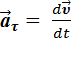 .
.
Направление вектора тангенциального ускорения  τ (см. рис. 16) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
τ (см. рис. 16) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
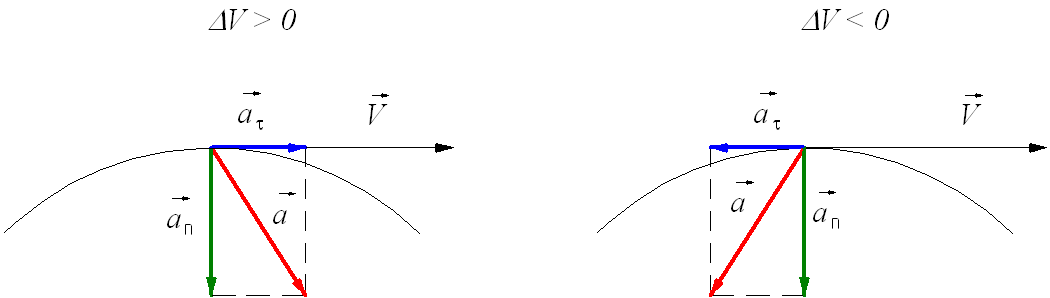
Рис. 16. Тангенциальное, нормальное и полное ускорения.
Нормальное (центростремительное) ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 15). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 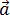 n. Вектор нормального ускорения направлен по радиусу кривизны траектории. Из рис. 15 видно, что
n. Вектор нормального ускорения направлен по радиусу кривизны траектории. Из рис. 15 видно, что 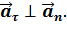
Криволинейное движение можно представить как движение по дугам окружностей (рис. 17).
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:
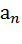 =
= 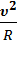 .
.
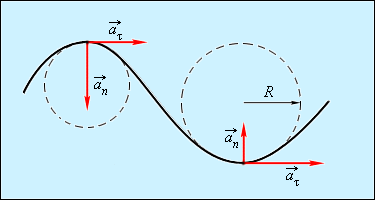
Рис. 17.
Движение по дугам окружностей.
Равнопеременное криволинейное движение
Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: aτ = const. Найдем закон этого движения, считая, что при t = 0: s = s0, а  =
=  0, где
0, где  0 – начальная скорость точки. Согласно формуле
0 – начальная скорость точки. Согласно формуле 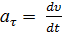 имеем: d
имеем: d 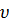 = aτ dt.
= aτ dt.
Так как aτ = const, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
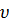 =
= 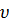 0+aτ t.
0+aτ t.
Формулу представим в виде: 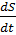 =
= 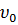 + aτ t или dS =
+ aτ t или dS = 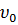 dt + aτ tdt.
dt + aτ tdt.
Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде: S = S0 + 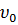 t +
t + 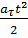 .
.
Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает – замедленным.
В частном случае при движение по окружности расположение векторов ускорений приведено на рис. 18.
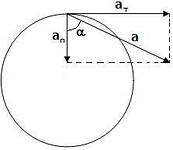
Рис. 18.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
 =
=  τ +
τ + 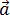 n ..
n .. Вектор 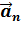 всегда направлен к центру окружности. Из рис. 15 видно, что модуль полного ускорения равен (согласно теореме Пифагора для прямоугольно прямоугольника): a =
всегда направлен к центру окружности. Из рис. 15 видно, что модуль полного ускорения равен (согласно теореме Пифагора для прямоугольно прямоугольника): a = 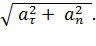
Пример . Движение точки задано уравнениями x=2t, y=3-4t2. Найти ускорение а точки.
Решение
Из первого уравнения t=x/2. Подставив во второе, получим уравнение траектории: y = 3 – x.2
Это уравнение параболы. В начале движения, при t=0, точка находилась на самом верху, в положении M 0 (x0=0, y0=3 см).
А, например, при t =0,5 c она будет в положении M с координатами x1=1 см; y1=2 см.
Проекции скорости на оси 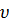 x=
x= 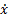 = 2см∙с-1,
= 2см∙с-1, 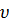 y=
y= 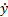 = -8t см∙с-1.
= -8t см∙с-1.
При t =0,5 c, 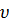 x = 2см∙с-1,
x = 2см∙с-1, 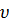 y = - 4 см∙с-1.
y = - 4 см∙с-1.
И модуль скорости: 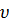 =
= 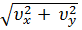 =
= 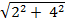 = 4,47
= 4,47  .
.
Составляющие скорости по осям и вектор её показаны в масштабе на рис. 19.

Рис.19.
Проекции ускорения ax = 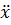 = 0, ay =
= 0, ay = 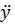 =
= 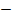 8
8 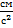 . Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
Ускорение – величина абсолютная, т.е. не зависит от выбора инерциальной системы отсчета.
Свободное падение тел. Ускорение свободного падения
Свободное падение – это движение тела под действием только силы тяжести.
На тело, падающее в воздухе, кроме силы тяжести действует сила сопротивления воздуха, следовательно, такое движение не является свободным падением. Свободное падение — это падение тел в вакууме.
Ускорение 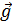 , которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.
, которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.
Ускорение свободного падения 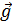 направлено вертикально вниз.
направлено вертикально вниз.
Галилео Галилей установил (закон Галилея): все тела падают на поверхность Земли под действием земного притяжения при отсутствии сил сопротивления с одинаковым ускорением, т.е. ускорение свободного падения не зависит от массы тела.
Убедиться в этом можно, используя трубку Ньютона или стробоскопический метод.
Трубка Ньютона представляет собой стеклянную трубку длиной около 1 м, один конец которой запаян, а другой снабжен краном (рис. 20).
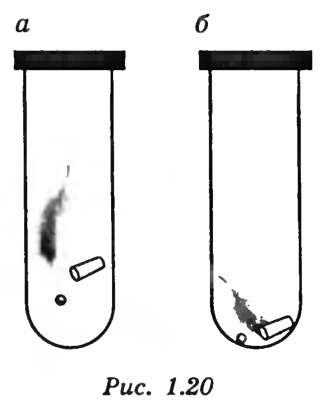
Рис.20.
Поместим в трубку три разных предмета, например дробинку, пробку и птичье перо. Затем быстро перевернем трубку. Все три тела упадут на дно трубки, но в разное время: сначала дробинка, затем пробка и, наконец, перо. Но так падают тела в том случае, когда в трубке есть воздух. Стоит только воздух откачать насосом и снова перевернуть трубку, мы увидим, что все три тела упадут одновременно.
В земных условиях g зависит от географической широты местности.
Наибольшее значение оно имеет на полюсе g = 9,81 м/с2, наименьшее — на экваторе g = 9,75 м/с2. Причины этого:
1) суточное вращение Земли вокруг своей оси;
2) отклонение формы Земли от сферической;
3) неоднородное распределение плотности земных пород.
Ускорение свободного падения зависит от высоты h тела над поверхностью планеты. Его, если пренебречь вращением планеты, можно рассчитать по формуле:
gh = 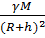
где 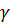 — гравитационная постоянная, М — масса планеты, R — радиус планеты.
— гравитационная постоянная, М — масса планеты, R — радиус планеты.
Как следует из последней формулы, с увеличением высоты подъема тела над поверхностью планеты ускорение свободного падения уменьшается. Если пренебречь вращением планеты, то на поверхности планеты радиусом R: g = 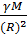 .
.
Для небольших высот (g << h) можно считать g = const, для таких высот свободное падение является равноускоренным движением.
Для его описания можно использовать формулы равноускоренного движения:
- уравнение скорости: 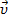 =
= 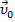 +
+ 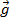 t ,
t ,
- кинематическое уравнение, описывающее свободное падение тел:
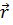 = r0 +
= r0 + 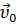 t +
t + 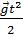
или в проекции на ось: y = y0 + 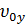 t +
t + 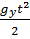 .
.
Поступательное движение твёрдого тела
Поступательное движение твёрдого тела – это движение, при котором прямая, соединяющая две любые точки тела, перемещается, оставаясь параллельной своему начальному направлению (рис. 21).
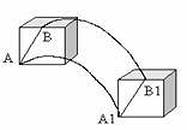
Рис. 21.
При таком движении все точки тела описывают одинаковые траектории и имеют одинаковые скорости и ускорения. Поэтому кинематическое рассмотрение поступательного движения твёрдого тела сводится к изучению движения любой его точки, как правило, центра масс (т.С).
Понятие о степенях свободы
Минимальное число параметров, задание которых полностью определяет положение тела в пространстве, называется числомего степеней свободыi.
Примеры.
· Простейшая механическая система — материальная точка в трёхмерном пространстве — обладает тремя степенями свободы, так как её состояние полностью описывается тремя пространственными координатами (рис.2), т.е. i=3.
· Абсолютно твёрдое тело обладает шестью степенями свободы, так как для полного описания положения такого тела достаточно задать три координаты центра масс и три угла, описывающих ориентацию тела (эти величины известны в быту как «наклон, подъём, поворот», в авиации их называют «крен, тангаж, рыскание»), т.е. i = iпост. + iвр. = 6, где iпост. = 3 – число степеней свободы поступательного движения центра масс тела; iвр. = 3 – число степеней свободы вращательного движения тела.
· Реальные тела обладают огромным числом степеней свободы (порядка числа частиц, из которых состоит тело). Однако в большинстве ситуаций оказывается, что наиболее важны лишь несколько «коллективных» степеней свободы, характеризующих движение центра масс тела, вращение тела, его деформацию, его макроскопические колебания. Остальные же — микроскопические — степени свободы не заметны по отдельности, а воспринимаются сразу все вместе, как, например, температура и давление.
Любая связь уменьшает степень свободы системы на единицу.
Пример.
Гармонические колебания математического маятника (рис. 22) задаются углом отклонения  от положения равновесия, т.е. i = 1.
от положения равновесия, т.е. i = 1.
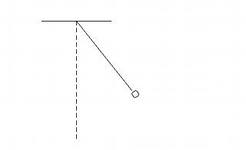
Рис. 22.
Вращательное движение твёрдого тела вокруг неподвижной оси задаётся углом поворота  (рис. 23), т.е. i = 1.
(рис. 23), т.е. i = 1.
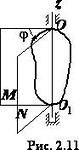
Рис. 23.
