Изучение законов колебательного движения
Цель работы: изучение колебательного движения тел на примере математического и физического маятников, определение ускорения свободного падения.
Приборы и принадлежности: математический маятник, оборотный маятник, электронный счетчик-секундомер.
Теоретические сведения
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Дифференциальное уравнение гармонических колебаний:
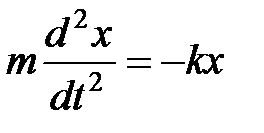
или
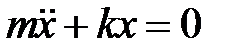 , (1)
, (1)
где m – масса колеблющейся системы; х – смещение этой системы от положения равновесия; k – коэффициент упругости; 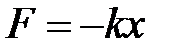 – возвращающая сила.
– возвращающая сила.
Решением дифференциального уравнения (1) является уравнение колебательного движения, которое определяют выражением
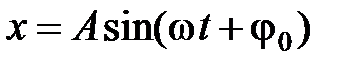 .
.
где х – изменяющаяся величина; t – время; А – амплитуда колебаний, т.е. максимальное отклонение колеблющейся величины от положения равновесия (рис.1); 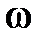 - циклическая (круговая) частота;
- циклическая (круговая) частота; 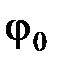 - начальная фаза.
- начальная фаза.
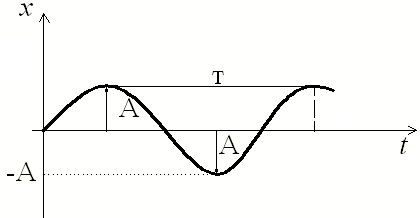 Рис.1 Рис.1 | Физический смысл циклической частоты состоит в том, что она численно равна числу полных колебаний, совершаемых за 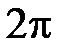 секунд, т.е секунд, т.е 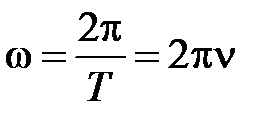 , где Т – период колебаний, т.е. время, за которое совершается одно полное колебание; , где Т – период колебаний, т.е. время, за которое совершается одно полное колебание; 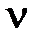 – частота колебаний, т.е. число полных колебаний, совершаемых за единицу времени; – частота колебаний, т.е. число полных колебаний, совершаемых за единицу времени; 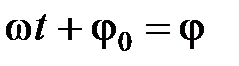 – фаза колебания в момент времени t. – фаза колебания в момент времени t. |
Фаза колебания – функция времени, она определяет значение изменяющего параметра (х – смещения; 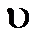 – скорости; а – ускорения) в данный момент времени. Например, фаза определяет, какую часть от амплитуды А составляет смещение х в данный момент времени:
– скорости; а – ускорения) в данный момент времени. Например, фаза определяет, какую часть от амплитуды А составляет смещение х в данный момент времени:
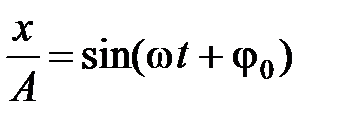 ,
,
где 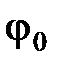 – начальная фаза колебания, т.е. фаза в момент времени t=0.
– начальная фаза колебания, т.е. фаза в момент времени t=0.
Если система совершает колебания около положения равновесия без воздействия внешних сил за счет первоначально сообщенной энергии, то такие колебания называются собственными или свободными. Дифференциальное уравнение свободных гармонических колебаний с учетом собственной частоты колебаний 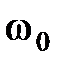
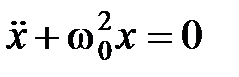 . (2)
. (2)
В качестве примера свободных колебаний рассмотрим колебания математического и физического маятников.
Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести (рис. 2, а).
В положении равновесия (точка А) сила тяжести 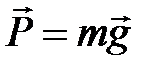 уравновешивается силой натяжения нити
уравновешивается силой натяжения нити 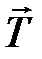 . Если маятник отклонить от положения равновесия в точку С на некоторый угол α, то составляющая силы
. Если маятник отклонить от положения равновесия в точку С на некоторый угол α, то составляющая силы 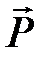 , направленная вдоль нити
, направленная вдоль нити 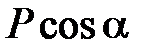 , уравновесится силой натяжения нити
, уравновесится силой натяжения нити 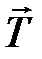 , а другая составляющая силы тяжести
, а другая составляющая силы тяжести 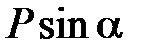 , перпендикулярная нити, стремится вернуть маятник в положение равновесия. Эта сила является возвращающей силой, или квазиупругой силой. Квазиупругая сила – сила, не упругая по своей природе, но аналогичная упругой силе по виду ее зависимости от смещения, она всегда направлена в сторону, противоположную смещению, и при малых углах отклонения α пропорциональна смещению х.
, перпендикулярная нити, стремится вернуть маятник в положение равновесия. Эта сила является возвращающей силой, или квазиупругой силой. Квазиупругая сила – сила, не упругая по своей природе, но аналогичная упругой силе по виду ее зависимости от смещения, она всегда направлена в сторону, противоположную смещению, и при малых углах отклонения α пропорциональна смещению х.
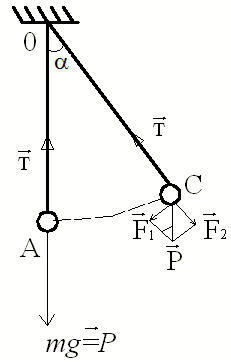 |  |
| а | б |
| Рис. 2 |
В точке С на маятник действует вращающий момент
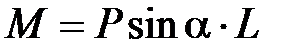 , (3)
, (3)
где L – плечо силы 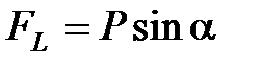 .
.
По основному закону динамики вращательного движения
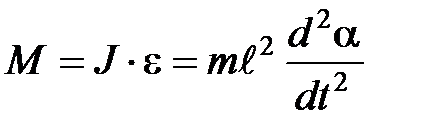 (4)
(4)
где 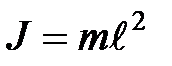 – момент инерции материальной точки;
– момент инерции материальной точки; 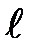 - длина нити. Приравнивая формулы (3) и (4), получим
- длина нити. Приравнивая формулы (3) и (4), получим
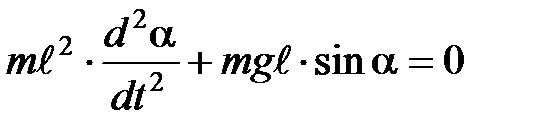
или 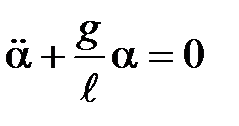 (5)
(5)
Полученное уравнение имеет вид, аналогичный дифференциальному уравнению (2), поэтому можно заменить 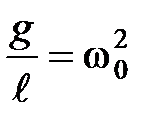 . Тогда период собственных колебаний математического маятника
. Тогда период собственных колебаний математического маятника
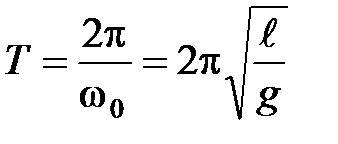 . (6)
. (6)
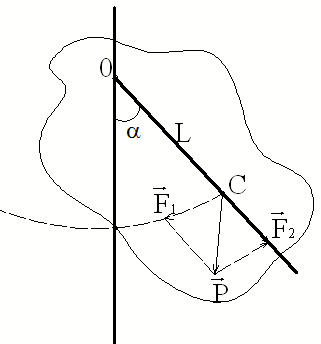
Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси подвеса О, не проходящей через центр масс тела С (рис. 2,б).
При отклонении маятника на угол α составляющая силы тяжести 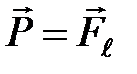
 стремится возвратить маятник в положение равновесия. Для малых углов
стремится возвратить маятник в положение равновесия. Для малых углов 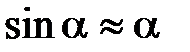
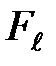
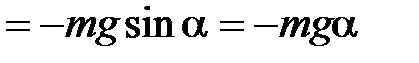 . (7)
. (7)
Возвращающий момент М, создаваемый силой 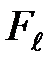
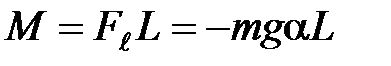 , (8)
, (8)
где L = OC – плечо силы 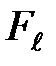 .
.
По основному закону динамики вращательного движения
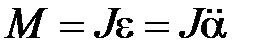 (9)
(9)
где J – момент инерции маятника относительно оси О.
Из формул (8) и (9) имеем
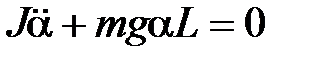 ,
,
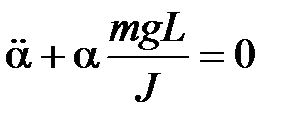 . (10)
. (10)
Уравнение (10) аналогично уравнениям (2) и (5), поэтому
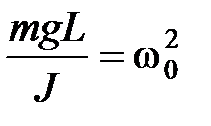 . (11)
. (11)
Отсюда период собственных колебаний физического маятника
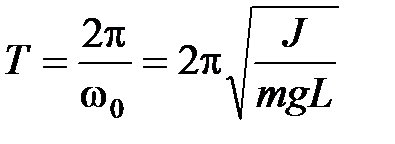 . (12)
. (12)
Выражение 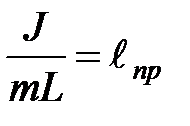 называется приведенной длиной физического маятника.
называется приведенной длиной физического маятника.
Приведенной длиной физического маятника называется длина некоторого воображаемого математического маятника, который имеет тот же период колебаний, что и данный физический маятник.
С учетом приведенной длины период колебаний физического маятника будет иметь вид
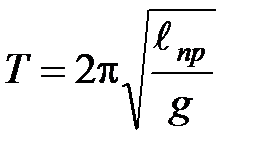 (13)
(13)
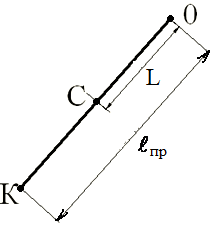 Рис. 3 Рис. 3 | Точка К на прямой, соединяющей точку подвеса О с центром тяжести С, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (рис. 3.). Приведенная длина 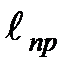 всегда больше L, поэтому точка подвеса и центр качания лежат по разные стороны от центра тяжести. всегда больше L, поэтому точка подвеса и центр качания лежат по разные стороны от центра тяжести. |
Точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. Следовательно, при переносе точки под веса в центр качания период колебаний маятника остается прежним. Это положение называется теоремой Гюйгенса.
Таким образом, если подобрать у физического маятника такие несимметричные относительно центра тяжести положения двух параллельных осей подвеса, чтобы период колебаний относительно них был одинаков, то расстояние между этими осями будет равно приведенной длине физического маятника. Измерив, это расстояние и период колебаний, можно по формуле (13) найти ускорение свободного падения g.
Описание установки
Маятник, имеющий две параллельные друг другу трехгранные призмы, на которые он может поочередно подвешиваться, называется оборотным маятником.
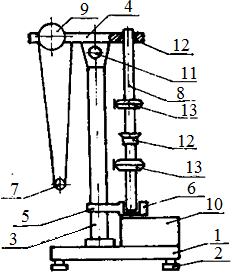
Общий вид установки, включающей в себя математический и оборотный маятники, показан на рис. 4, а.
 |  |
| а | б |
| Рис. 4 |
Основание 1 установки (рис. 4, б) оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 5 с фотоэлектрическим датчиком 6. После отвинчивания воротка 11 кронштейн можно поворачивать вокруг колонки. Натяжение воротка фиксирует кронштейн в любом, произвольно избранном положении. С одной стороны кронштейна 4 находится математический маятник 7, с другой - на вмонтированных вкладышах оборотный маятник 8.
Математический маятник представляет собой массивный шарик небольшого радиуса 7, подвешенный на длинной нити для того, чтобы колебания происходили строго в одной плоскости. Длину математического маятника можно регулировать при помощи воротка 9, а его величину можно определить при помощи колонки 3.
Оборотный маятник представляет собой стальной стержень 8, на котором могут перемещаться и закрепляться в различных положениях опорные призмы 12 и тяжелые чечевицы 13. Призмы и чечевицы закрепляются приблизительно так, как показано на рис.4,б и маятник подвешивается на кронштейне 4 на одной из призм.
На стержне через 10 мм выполнены кольцевые нарезания, служащие для точного определения длины оборотного маятника (расстояние между призмами 12).
Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки и фиксировать в произвольно избранном положении. Фотоэлектрический датчик соединен разъемом с привинченным к основанию универсальным миллисекундомером 10.
Порядок выполнения работы
Задание 1. Определение ускорения свободного падения с помощью
оборотного маятника.
1. Закрепить чечевицы 13 на стержне оборотного маятника несимметрично, т.е. таким образом, чтобы одна из них находилась вблизи конца стержня, а другая вблизи его середины Призмы маятника 12 закрепить по обеим сторонам центра тяжести, чтобы они были обращены друг к другу лезвиями. Одну из них поместить вблизи свободного конца, а вторую на половине расстояния между чечевицами. Проверить, отвечают ли грани лезвий призм нарезаниям на стержне
2. Закрепить маятник на верхнем кронштейне на грани призмы, находящейся вблизи конца стержня.
3. Нижний кронштейн вместе с фотоэлектрическим датчиком закрепить так, чтобы стержень маятника пересекал оптическую ось.
4. Отклонить маятник на 4-5° от положения равновесия и отпустить. Нажать клавишу "сброс", после подсчета измерителем 9-ти полных колебаний нажать клавишу "стоп". Секундомер покажет время 10 полных колебаний.
5. Повторить пятикратные измерения времени колебания. Результаты измерений записать в табл. 1.
6. Рассчитать период колебаний оборотного маятника Тоб по формуле
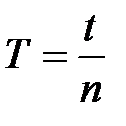 . (14)
. (14)
7. Снять маятник и закрепить его на второй призме, которая находится посередине стержня. Нижний кронштейн с фотоэлектрическим датчиком переместить так, чтобы маятник пересекал оптическую ось.
8. Отклонить маятник на 4-5° от положения равновесия, измерить время колебания t и сравнить полученный результат со средним временем колебания tоб.
9. Если t > tоб, то вторую призму, расположенную между чечевицами, переместить в направлении чечевицы, находящейся в конце стержня. Если t<tоб, то - в направлении середины стержня. Размещение чечевиц не менять.
10. Повторно измерить время колебаний и сравнить с величиной tоб. Изменять положение второй призмы до момента получения равенства t = tоб с точностью до 0,5%.
11. Получив равенство во времени, повторить пятикратно измерение времени колебания t. Результаты записать в табл.1.
12. Рассчитать период колебаний маятника Тф и занести в табл.1.
13. Определить приведенную длину оборотного маятника 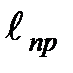 , подсчитывая количество нарезаний на стержне между призмами, которые нанесены через каждые 10 мм.
, подсчитывая количество нарезаний на стержне между призмами, которые нанесены через каждые 10 мм.
Таблица 1
| n | Призма находится в конце стержня | Призма находится в середине стержня | 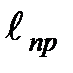 , cм , cм | ||||
| N | t, c | Tоб, c | n | t, c | Tф, c | ||
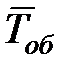 , с , с | 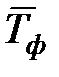 , с , с |
14.Определить ускорение свободного падения gф по формуле
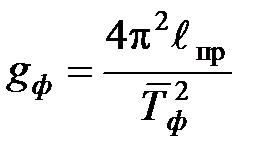 .
.
15. Рассчитать абсолютную ошибку измерения ускорения свободного падения g по формулам
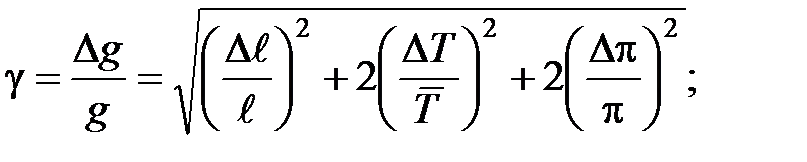 (15)
(15)
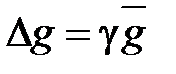 . (16)
. (16)
16. Записать окончательный результат в виде 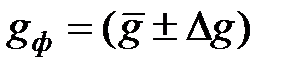 , при α = 0,95.
, при α = 0,95.
Задание 2. Определение ускорения свободного падения
с помощью математического маятника.
1.Поворачивая верхний кронштейн, поместить над фотоэлектрическим датчиком математический маятник.
2. Вращая вороток на верхнем кронштейне, установить длину математического маятника 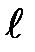 , равную приведенной длине оборотного маятника
, равную приведенной длине оборотного маятника 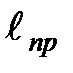 (определенной в задании 1). Обратить внимание на то, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика.
(определенной в задании 1). Обратить внимание на то, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика.
3. Ввести математический маятник в движение, отклоняя шарик на 4-5° от положения покоя.
4. Нажать кнопку "сброс". После подсчета измерителем 9-ти колебаний нажать кнопку "стоп". Результат времени записать в табл. 2.
5. Пятикратно повторить измерение времени колебания и занести в табл. 2.
6. Рассчитать период Тм математического маятника по формуле (14). Сравнить периоды колебаний математического маятника с физическим, вы вычисленным выше.
Таблица 2
| N | 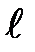 , см , см | n | t, c | Tм, c | Tф, c | ΔT, c |
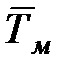 , с , с |
7. Рассчитать ускорение свободного падения по формуле
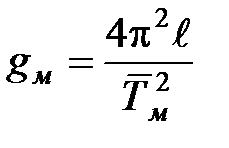
8. Вычислить абсолютную ошибку для ускорения свободного падения gм по формулам (15), (16).
9. Записать окончательный результат в виде 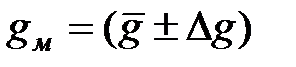 , при α = 0,95.
, при α = 0,95.
10. Сравнить величины ускорения свободного падения, полученные с помощью математического и физического маятников и сделать соответствующие выводы.
Контрольные вопросы
1. Дать определение понятий: гармоническое колебание, амплитуда, частота, период, фаза, начальная фаза. Записать уравнение гармонического колебания.
2. Нарисовать графики гармонических колебаний, отличающихся друг от друга:
- амплитудой,
- частотой,
- фазой,
- начальной фазой.
3. Как определить скорость, ускорение, энергию колеблющейся точки?
4. Что называется физическим маятником, математическим маятником, приведенной длиной физического маятника?
5. Вывести формулы периода колебаний физического и математического маятников. Сравнить их.
6. Сформулировать теорему Гюйгенса. Рассказать, где она применяется в данной работе.
ЛАБОРАТОРНАЯ РАБОТА №7
