Определение отношения теплоемкостей воздуха методом адиабатического сжатия и расширения

Оборудование: установка Клемана-Дезорма.

Теоретическое введение

Внутренняя энергия одного моля идеального газа может быть выражена уравнением:

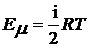, (1)

где: R - универсальная газовая постоянная, T - абсолютная температура, i - число степеней свободы.

Числом степеней свободы твердого тела называют число независимых координат, с помощью которых можно полностью описать его положение в пространстве. В общем случае молекула газа, рассматриваемая в виде жестко связанных атомов, может перемещаться в пространстве совершенно произвольно, т.е. участвовать в шести одновременных независимых движениях (рисунок 1) трех вращательных вокруг трех взаимно перпендикулярных осей ά, β, γ, проходящих через центр тяжести молекулы, и трех поступательных движений вдоль трех осей прямоугольной системы координат x, y, z. Таким образом в общем случае молекула газа может иметь шесть степеней свободы: три поступательных и три вращательных. Однако молекулы содержат различное число атомов, что и отражается на общем числе степеней свободы.

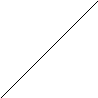
Частица одноатомного газа рас- z γ β

сматривается в виде материальной

точки. Поступательное движение та- α

кой точки определяется тремя коор-

динатами, а при ее вращении она не x

изменяет своего положения в прост- y Рисунок 1

ранстве. Следовательно, частица одноатомного газа имеет три поступательные степени свободы.

Двухатомную молекулу можно представить в виде двух жестко связанных между собой атомов (рисунок 3а). Такая молекула будет иметь три поступательные степени свободы и две вращательные вокруг двух осей β, γ перпендикулярных к линии связи между атомами. При вращении вокруг оси α совпадающей с линией связи, двухатомная молекула не меняет своего положения в пространстве. Таким образом двухатомная молекула имеет пять степеней свободы: три поступательных и две вращательных.

В трехатомной молекуле все атомы жестко связаны между собой (рисунок 3б). Такая молекула будет иметь шесть степеней свободы: три пос­тупательных и три вращательных. Такое же число степеней свободы будет иметь и все молекулы с числом атомов больше трех. После этого отступ­ления возвратимся вновь к рассматриваемому вопросу о внутренней энергии газа.

Приращение внутренней энергии газа ΔЕ при изменении его темпера­туры на ∆Т в соответствии с равенством (1) примет вид:

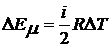. (2)

Если идеальный газ нагревается при постоянном объеме, то вся подведенная теплота затрачивается на увеличение его внутренней энергии.

Отношение приращения внутренней энергии ΔЕ_µ к изменению температуры ΔТ, вызвавшему это приращение энергии, называют мольной теплоемкостью:

.

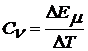Вставляя в это равенство значение ΔЕ_µ из (2), получим:

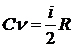. (3)

Если идеальный газ нагревается при постоянном давлении, то в этом случае затрачивается дополнительное количество тепла, идущее на совер­шение работы при расширении газа. Следовательно мольная теплоемкость газа при постоянном давлении С_p будет больше его теплоемкости С_v на величину внешней работы А, т.е. C_p = C_v + A.

Величина А = Р ΔV = Р ( V_μ' - V_μ ), где: Р - давление, V_μ'- мольный обьм газа после нагревания на один градус, V_μ- мольный обьем газа при температуре Т , т.е. при Т+1 = Т'.

По уравнению Клапейрона-Менделеева значения РV_μ и РV_μ' для температур Т и Т' выразится так

РV_μ = RT и РV_μ'=R(T + 1).

Вставляя эти значения в выражение работы А, а затем в уравнение теплоемкости С_р получим

С_р= С_ν + R. (4 )

Выражение (4) называется уравнением Майера.

Отношение теплоемкостей γ=С_р/ С_ν в соответствии с равенствами (3) и (4) примет вид

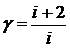. (5)

Полученное соотношение теплоемкостей (5) в дальнейшем будет применено для сопоставления с результатами экспериментального измерения.