Гидравлический удар в трубах
Резкое повышение давления воды в трубах при внезапном перекрытии трубопровода было известно в водопроводной технике давно; это явление было названо "гидравлическим ударом" (потому что оно часто сопровождается появлением звука, сходного со звуком при ударе молотка по твердому телу, а иногда и сильным сотрясением трубы).
Теоретические исследования явления гидравлического удара были начаты также давно, однако только в конце прошлого столетия эта задача была решена Н.Е. Жуковским.
Исследования Н.Е. Жуковского показали, что гидравлический удар представляет собой сложный физический процесс и что все явления гидравлического удара объясняются возникновением и распространением ударной волны, происходящей от сжатия воды и расширения стенок трубы.
Упрощенно (пренебрегая рядом факторов, и в том числе потерями напора) процесс гидравлического удара можно представить себе так.
Пусть из резервуара большой емкости выходит горизонтальная труба, по которой в стационарных условиях протекает вода со скоростью u. На расстоянии l от входного сечения находится задвижка, которую можно закрыть как угодно быстро. Предположим это закрытие мгновенным. Тогда частицы жидкости, которые непосредственно соприкасаются с поверхностью задвижки, мгновенно остановятся, затем остановится ближайший к ним слой жидкости. Произойдет очень быстрое сжатие этого слоя, и давление в нем увеличится. Назовем это увеличение давления ударным давлением. Затем остановится и сожмется следующий слой жидкости, и в нем также увеличится давление; далее сжатие будет распространяться по всей длине трубы в направлении от задвижки к резервуару.
Пусть за интервал времени Δtповышенное, т.е. ударное давление достигнет резервуара. Если обозначить расстояние от резервуара до задвижки через l, то скорость распространения ударного давления
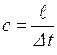 | (4.27) |
Величину с называют скоростью ударной волны.
В момент достижения ударной волной входного отверстия (т.е. резервуара) вся вода в трубе окажется сжатой, скорости всех частиц равными нулю и давление повышенным против первоначального, т.е. большим давления, обусловливаемого уровнем воды в резервуаре. Поэтому начнется отток жидкости из трубы в резервуар и постепенно вся жидкость в трубе придет в движение в направлении к резервуару; при этом давление будет уменьшаться до его первоначального значения. Когда это давление достигает задвижки, жидкость движется в трубе в сторону резервуара с некоторой скоростью, после чего начинается ее послойная остановка (начиная с сечения у задвижки) с понижением давления. Когда скорость во всей трубе станет равной нулю, пониженное давление достигнет входного сечения трубы; после этого наступит стадия послойного восстановления движения с первоначальной скоростью в сторону задвижки. Через промежуток времени Δtэту начальную скоростьu приобретает последний у задвижки слой жидкости, и так как задвижка является препятствием для передвижения жидкости, то снова возникнет "гидравлический удар", т.е. описанное явление повторится.
 Рисунок 4.2 – Гидравлический удар - Схема гидравлического удара Рисунок 4.2 – Гидравлический удар - Схема гидравлического удара |
В действительности явление удара гораздо более сложное, так как стенки трубы обладают упругостью (расширяются и сжимаются при изменениях давления в жидкости); жидкость также обладает упругостью, и, кроме того, в потоке возникают сопротивления движению жидкости, в результате чего колебания давления в трубе затухают. Расчеты этих колебаний довольно сложны, и мы их здесь не будем касаться, ограничиваясь определением повышения давления Δp в горизонтальной трубе у задвижки при мгновенном ее закрытии. С этой целью составим уравнение изменения количества движения, которое формулируется следующим образом: изменение количества движения равно импульсу силы и записывается:
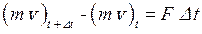 | (4.28) |
где m – масса жидкости;
v – скорость жидкости;
mv – количество движения;
F – сила действующая на жидкости;
∆t – время действия силы.
F∆t – импуль силы.
Масса жидкости в трубе m = rlπd2/4, скорость жидкости до прохождения ударной воды равна v, а после прохождения равно нулю. Давление у задвижки повышенное ∆p, а у входа в трубу повышения давления нет, поэтому во время прохождения ударной волны на жидкость действует сила F = - ∆p p d2/4. Знак минус указывает на то, что сила действует против направления движения жидкости. Повставим данные величины в уравнение (4.18):
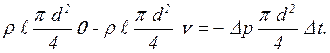 | (4.29) |
Из последнего уравнения найдём повышение давления:
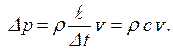 | (4.30) |
Это есть формула Н.Е. Жуковского для определения величины гидравлического удара.
Из этой формулы следует, что величина ударного давления зависит от начальной скорости движения воды в трубе и от скорости распространения ударной волны.
В то же время скорость с зависит от упругих свойств жидкости и от упругих свойств трубопровода. Действительно, при повышении давления сжимается только жидкость, но и происходит деформация трубопровода, его диаметр увеличивается. С учётом этих свойств скорость распространения ударной волны рассчитывается по формуле:
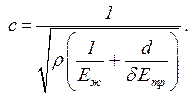 | (4.31) |
где Eж – модуль упругости жидкости;
Eтр – модуль упругости материала трубопровода;
d – внутренний диаметр трубопровода;
d – толщина стенок трубопровода.
Для нефтепроводов СМН внешним диаметром 820 мм толщина стенок трубы может составлять [9] 8, 9, 10, 11, 12 мм. Для стальных труб плотностью 7850 кг/м3 модуль упругости материала E = 206000 МПа. По нефтепроводу перекачиваются нефти с различными свойствами, поэтому модуль упругости нефти меняется. Среднее значение модуль упругости нефти [9] Eтр =1,3 109 Па. Средняя плотность нефти ro = 860 кг/м3. Расчётные скорости распространения звука в нефтепроводе приведены в таблице 1.1.
Таблица 4.3 -Значения скоростей распространения звука в нефтепроводе внешним диаметром 820 мм
| Таблица 4.4 -Значения скоростей распространения звука в нефтепроводе внешним диаметром 820 мм | |||
| Dн, мм | d, мм | do, мм | c, м/с |
| 961,8 | |||
| 983,6 | |||
| 1002,2 | |||
| 1018,3 | |||
| 1032,3 |
Если бы стенки трубы были абсолютно жесткими, то скорость распространения ударной волны совпадала бы со скоростью распространения звука в жидкости.
Таблица 4.5 -схемы распространения волн давления
| № | Действие | Изменение давления по длине нефтепровода | |||
| Прикрытие задвижки |
| ||||
| Открытие задвижки |  | ||||
| Закачка в нефтепровод |  | ||||
| Отбор из нефтепровода |  | ||||
| Отбор из нефтепровода с последующим прекращением отбора |  |
Явление гидравлического удара носит периодический характер. Действительно, после достижения резервуара ударная волна отразится и со скоростью с будет распространяться к задвижке. Общее время пробега прямой и отраженной (обратной) ударных волн составляет длительность фазы гидравлического удара Tф=2l/c. Далее циклы повышений и понижений давления будут чередоваться с промежутками времени Tф до тех пор, пока под влиянием гидравлических сопротивлений этот колебательный процесс не затухнет.
Рассмотренные выше решения справедливы при мгновенном закрытии задвижки (tз =0). Если время полного закрытия задвижки tз больше, чем длительность фазы гидравлического удара Tф, то повышение давления в этом случае можно определять по формуле
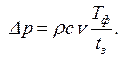 | (4.30) |
Для предохранения трубопровода следует или не допускать быстрых закрытий запорных устройств трубопроводов, или устанавливать демпфирующие воздушные колпаки. Для газопроводов и воздуховодов величина гидравлического удара обычно мала.
Примеры и задачи
Пример 4.1.
Насос перекачивает мазут по всасывающей линии трубопровода длиной ℓ, диаметром d и шероховатостью поверхности трубы 0,1 мм. Уровень жидкости в баке H, показание вакуума на входе в насос pv, а ртутного манометра hрт, коэффициент местных сопротивлений xм = 2,5.
Рассчитать расход Q.
Дано: вязкость 75 мПа∙с, плотность 890 кг/м3, ℓ = 7 м,d = 150 мм, H = 4 м,pv = 50 кПа, hрт =100 мм.
Решение:
Если жидкость несжимаемая, то силы инерции учитываются инерционным напором. Тогда для горизонтального трубопровода Ź1=Ź2, постоянного диаметра v1=v2, после выключения насоса р1=р2=ра, уравнение Бернулли для
Пример 5.2.
Центральный насос перекачивает нефть с кинематическим коэффициентом вязкости 3,5*10-5 м2/с по горизонтальному трубопроводу длиной 100м, диаметром 200мм и расходом 10 л/с. После выключения центробежного насоса давления на входе в насос и на выходе из трубопровода упало до атмосферного. Потерями напора в насосе и сжимаемостью нефти пренебречь. Найти закон изменения скорости жидкости в трубопроводе.
Решение :
Если жидкость несжимаемая, то силы инерции учитываются инерционным напором. Тогда для горизонтального трубопровода Ź1=Ź2, постоянного диаметра v1=v2, после выключения насоса р1=р2=ра, уравнение Бернулли для нестационарного движения запишется :
hτ +hi=0
Так как режим движения ламинарный:
Re= v*d = 4Q = 4 * 10-2 =1.81· 103 <Reкр=2000
υ πdυ 3.14 * 0.2 * 3.5 * 10 -3
потери напора на трение определяются по формуле(5.9):
hτ=128lυQ = 32lυ v,
πd4g d2g
а инерционный напор по формуле (10.7),тогда :
32 l υ v + l ∂ v = 0
d2g g ∂ t
Интегрируя это выражение при условии
t=0; v=vo= 4Q = 4 * 10 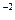 =0.318 м/с
=0.318 м/с
πd2 3.14 * (0.2)2
получаем v=vo l-32υt/d 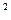 =0.318 * l-0.028t м/с
=0.318 * l-0.028t м/с
Пример 4.3.
Найти потери давления при движении воздуха в вентиляционном канале 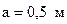 ,
, 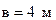 при температуре
при температуре 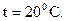 Расход воздуха при заданных условиях
Расход воздуха при заданных условиях 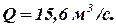
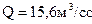
Решение:
Заданному состоянию воздуха соответствует кинематический коэффициент вязкости 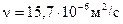 и плотность
и плотность 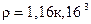
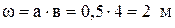
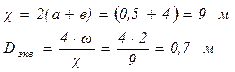
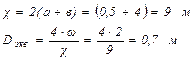
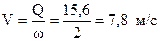
Находим число Рейнольдса, характеризующее поток воздуха в канале:
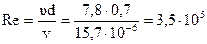
Определим относительную шероховатость канала (при абсолютной эквивалентной шероховатости 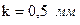 ):
):
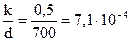
Находим величину коэффициента гидравлического трения по обобщенной формуле
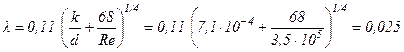
Определяем потерю полного давления на 1 пог. м канала:
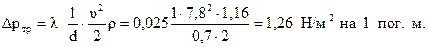
Пример 4.4.
Воздух при t=2°C движется по трубопроводу диаметром d=0,1м и длиной 15км. Давление в начале трубопровода 4,41Мпа, а в конце 0,29 Мпа. Определить массовый расход. Трубопровод изготовлен из новых стальных сварных труб.
Решение задачи.
Используем формулу (53).
Здесь неизвестны плотность газа в начале трубопровода r1 и коэффициент трения.
Определяем плотность газа в начале трубопровода.
r1 =р1/RT =4,41×106/287/275=56,6кг/м3.
Здесь R=287 – газовая постоянная для воздуха, T=273+2=275 –абсолютная температура.
Предполагаем турбулентный режим движения, задаемся величиной
l =0,02 и вычисляем в первом приближении массовый расход:
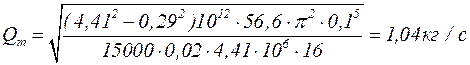 .
.
Определяем число Re и режим движения газа:
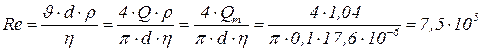 .
.
Коэффициент динамической вязкости определяем по справочным данным.
При р=98кПа и t=2°C - n=13,9×10-6м2/с, плотность r=1,27кг/м3, следовательно:
h = n×r = 13,9×10-6 × 1,27 = 17,6×10-6 Па×с.
Уточняем значение коэффициента трения. При турбулентном режиме:
l=0,11(68/Re+Dэ/d)0,25 = 0,11(68/7,5×105 +0,1×10-3/0,1)0,25 = 0.0199=0,02.
Для новых стальных сварных труб Dэ =0,1мм.
Таким образом, значение коэффициента трения практически не изменилось и массовый расход газа определен правильно.
Задача 4.1
При мгновенном закрытии задвижки давление в трубопроводе повышается на величину Δp. Как изменится повышение давления, если время закрытия задвижки составляет 1 с, 2 с, 3 с, 4 с. Длина трубопровода 1,2 км, а скорость звука в нем 1200 м/с.
Ответ. Не изменится; не изменится; уменьшается в 1,5 раза, в 2 раза.
Задача 4.2
По стальному трубопроводу длиной 1,5 км, диаметром 200 мм и толщиной стенок 6 мм перекачивается нефть плотностью 830 кг/м3 и модулем упругости 1,15 * 109 н/м2. Модуль упругости стали считать в 300 раз больше модуля упругости нефти. Определить скорость распространения гидравлического удара в трубопроводе и повышение давления в нем, если за время 5 с скорость нефти в трубопроводе уменьшилась на 1 м/с.
Ответ . 1120 м/с; Δp=0,498 106 Па
Задача 4.3
Клапан поршневого насоса, подающего жидкость в напорный трубопровод длиной 100м, диаметром 150 мм, срабатывает при расходе жидкости 1,5 10-3 м3/с. Определить изменение давления после клапана в напорной магистрали, если клапан закрылся за 0,1 с. Скорость распространения гидравлического удара 1200 м/с, а плотность жидкости 1000 кг/м3 .
Ответ : Δp=-1.02 105 Па
Задача 4.4
По трубопроводу длиной 3 км перекачивается жидкость со средней скоростью 3 м/с. На расстоянии 1км от входа в трубопровод находится задвижка, которая закрывается в течение 2-х секунд. Найти перепад давления на задвижке после ее закрытия, если скорость распространения гидравлического удара равна с=1300 м/с, а плотность жидкости 860 кг/м3.
Ответ: Δp=5,93 106 Па
Задача 4.5
При включении насоса расход жидкости меняется по линейному закону и за время to=5 с возрастает от нуля до 10-2 м3/с. Определить давление , которое должен создавать насос в любой момент времени 0<t<to для обеспечения заданного закона изменения подачи, если перекачивается жидкость плотностью 103 кг/м3 по горизонтальному трубопроводу длиной 5 км, диаметром 100 мм. Скорость распространения гидравлического удара равна 1400м/с. Потери напора не учитывать.
Ответ: Δp=0,356 105 t Па
Задача 4.6
По горизонтальному трубопроводу длиной 1 км, диаметром 200 мм центробежный насос перекачивает несжимаемую жидкость со средней скоростью vо=2 м/с. Определить закон изменения скорости жидкости со временем и скорость жидкости в момент времени t=5 с после остановки насоса. Коэффициент гидравлического сопротивления принять равным λ=0,02, а движение считать турбулентным.
Указание. При остановке насоса давление считать равным атмосферному.
Ответ: v=1.33 м/с v= vo
(1+λvo/2d*t)
Задача 4.7
Определить потери напора в газопроводе низкого давления, транспортирующем газ при 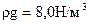 и
и 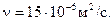 диаметр газопровода
диаметр газопровода 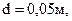 Расход газа
Расход газа 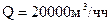 Длина участка l=
Длина участка l= 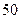 м.
м.
Задача 4.8
Определить потери давления в газопроводе высокого давления диаметром 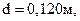 по которому транспортируется газ
по которому транспортируется газ 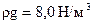 и
и 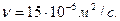 Абсолютное давление газа в начале участка
Абсолютное давление газа в начале участка 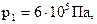 расход газа
расход газа 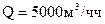 Длина участка газопровода
Длина участка газопровода