Экономические приложения дифференциальных уравнений.

Пусть y(t) – объем продукции некоторой отрасли, реализованной к моменту времени t. Будем полагать, что вся производимая отраслью продукция реализуется по некоторой фиксированной цене p, т.е. выполнено условие ненасыщаемости рынка. Тогда доход к моменту времени t составит .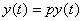

Обозначим через I(t) величину инвестиций, направляемых на расширение производства. В модели естественного роста полагают, что скорость выпуска продукции (акселерация) пропорциональна величине инвестиций, имеет место дифференциальное уравнение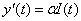

Полагая, что величина инвестиций I(t) составляет фиксированную часть дохода, получим 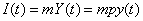, где коэффициент пропорциональности m (так называемая норма инвестиций) – постоянная величина, 0<m<1.

Подставляя последнее выражение для I(t) в дифференциальное уравнение, получим 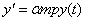, обозначим k= 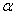mp, тогда .

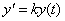Это дифференциальное уравнение – с разделяющимися переменными. Решим его:

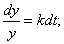
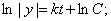
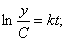
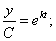
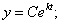
При начальных условиях 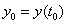решение можно записать в виде .

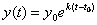Замечание. Уравнение 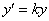описывает также рост народонаселения, динамику роста цен при постоянной инфляции, процесс радиоактивного распада и др.

На практике условие насыщаемости рынка может быть принято только для достаточно узкого времени интервала. В общем случае кривая спроса, т.е. зависимость цены реализованной продукции от ее объема является убывающей функцией p = p(y). Поэтому модель роста в условиях конкурентного рынка примет вид 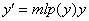оставаясь по-прежнему уравнением с разделяющимися переменными.

Так как все сомножители в правой части уравнения положительны, то 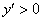, и это уравнение описывает возрастающую функцию y(t). При исследовании функции y(t) на выпуклость естественно используется понятие эластичности функции. Дифференцируя уравнение 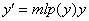получим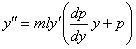

Так как эластичность спроса определяется формулой 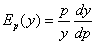, получим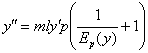

Условие 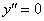равносильно равенству .

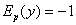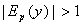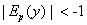Таким образом, если спрос эластичен, т.е. или , то 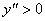и функция выпукла вниз; в случае если спрос эластичен, то функция выпукла вверх.

Пример. Найти выражение для объёма реализованной продукции 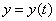, если известно, что кривая спроса 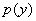задаётся уравнением 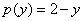, норма акселерации 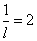, норма инвестиций , .

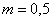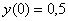Решение:

Используя формулу, отражающую модель роста в условиях конкурентного рынка

,

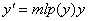получим

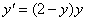
Решаем: разделим переменные:

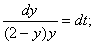
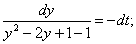
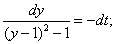
интегрируя, получим:

.

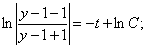
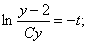
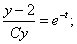
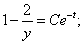
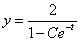Учитывая, что 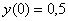, получаем, что .

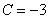Таким образом .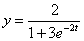

Пример 54 Найти функцию дохода 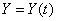, если известно, что величина потребления задаётся функцией 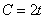, коэффициент капиталоёмкости прироста дохода , .

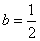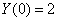Решение:

Известно, что функция дохода равна

,

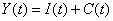где 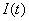– сумма инвестиций, 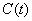– величина потребления.

А также имеет место дифференциальное уравнение

,

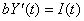где 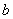– коэффициент капиталоёмкости прироста дохода. По условию задачи составим дифференциальное уравнение:

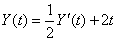, или

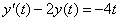
Итак, функция дохода удовлетворяет линейному неоднородному уравнению первого порядка. Будем искать его решение в виде .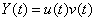

Тогда 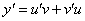, подставим в уравнение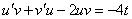

1) 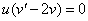2)

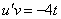
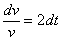
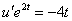
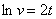
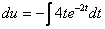
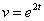
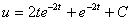
Общее решение 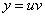или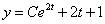

Используя начальные условия 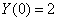, найдём 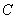: 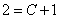или .

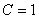Итак, функция дохода имеет вид .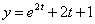

Начиная с середины 1950-х годов в макроэкономической теории

стали пользоваться неоклассическими моделями экономического роста, в частности моделями Солоу, в которых коэффициент капиталовооружённости 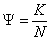(стоимость основного капитала, приходящаяся на одного занятого в производстве) есть ведичина переменная, меняется в зависимости от состояния экономической коньюнктуры.

Основное уравнение модели Солоу есть частное дифференциальное уравнение первого порядка

,

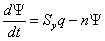где q – средняя производительность труда ( или стоимость дохода , произведённого одним работающим )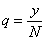

n – годовой темп прироста населения (условно 0<n<0,03)

Sy – функция сбережения, 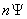– инвестиции.

Данное уравнение показывает, как должна изменяться во времени капиталовооружённость 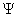труда , чтобы существующий равновесный рост обеспечивал полное использование производственных мощностей, и в том числе – полную занятость.

Именно при условии 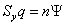будем иметь место равновесный рост с постоянной капиталовооружённостью и постоянной производительностью труда.

Эту закономерность легко пояснить на графике.

Если левая часть выражения больше правой 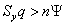, то сбережения превышают инвестиции, то есть приращение капитала, необходимого для поддержания соответствующего уровня капиталовооружённости 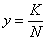. То есть в этом случае выполняется неравенство 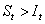, что требует повышения капиталоёмкости (от 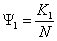до ).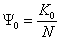

Напротив, если 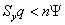, то для достижения равновесия экономики и полной занятости следует понизить капиталовооруженность труда 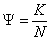, что автоматически достигается рыночными изменениями ценовых параметров.

На рисунке линия 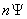– прямая, так как условно предполагается, что прирост населения постоянен, линия 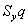– выпуклая.