Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Характеристическое уравнение. Вид общего решения однородного уравнения.

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.

Пусть дано ЛОДУ второго порядка

,

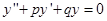Где p и q постоянны.

Для нахождения общего решения уравнения 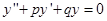достаточно найти два его частных решений, образующих фундаментальную систему.

Будем искать частные решения уравнения 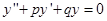в виде

,

где k – некоторое число. Дифференцируя эту функцию 2 раза и подставляя выражения для у, у’ и у’’ в уравнение 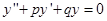, получим: 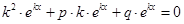, т.е.

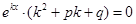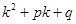, или =0 ( ).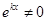

Уравнение 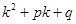=0 ( 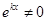) называется характеристическим уравнением ДУ .

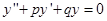При его решении возможны следующие три случая

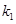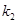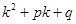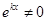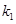
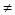
Случай 1: Корни уравнения и уравнения =0 ( ). Действительные и различные: 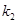(D = 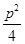- q > 0).

В этом случае частными решениями уравнения 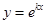являются функции =

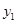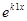
и 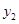= 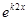. Они образуют фундаментальную систему решений (линейно независимы), т.к. их вронскиан

W(x) = =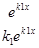

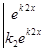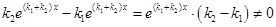
Следовательно, общее решение уравнения ,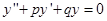

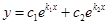
Случай 2: Корн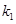и и 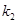характеристического уравнения 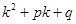=0 ( 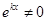), действительные равные: .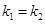

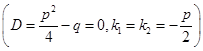В этом случае имеем лишь одно частное решение .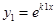

Покажем, что наряду с 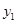решением уравнения 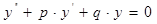будет и .

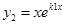Действительно, подставим функцию 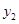в уравнение 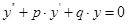. Имеем: +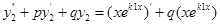

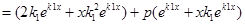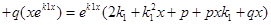
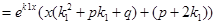
Но 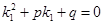, т.к. 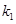есть корень уравнения 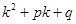=0 ( 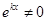) ; 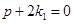, т.к. по условию .

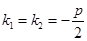Поэтому 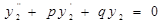, т.е. функция 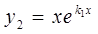является решением уравнения .

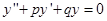Частные решения 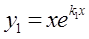и 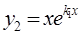образуют фундаментальную систему решений: 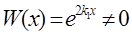. Следовательно, в этом случае общее решение ЛОДУ 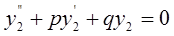имеет вид

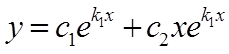
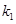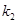Случай 3: Корни и уравнения 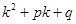=0 ( 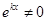) комплексные: ,

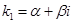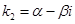
В этом случае частными решениями уравнения 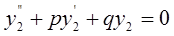являются функци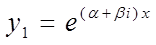и и .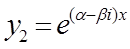

По формулам Эйлера:

,

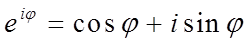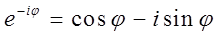
Имеем

,

.

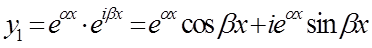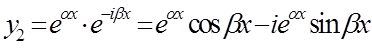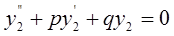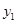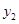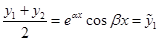Найдем два действительных частных решения уравнения . Для этого составим две линейные комбинации решений для и :

и .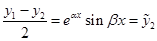

Функци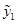и и 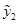являются решениями уравнения 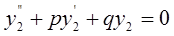, что следует из свойств решений ЛОДУ второго порядка. Эти решения 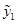и 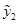образуют фундаментальную систему решений, т.к. 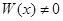. Поэтому общее решение данного уравнения запишется в виде 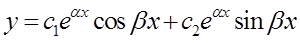или

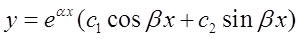
Экономические приложения интегралов

Традиционно практическое приложение интеграла иллюстрируется вычислением площадей различных фигур, нахождением объемов геометрических тел и некоторыми приложениями в физике и технике. Однако роль интеграла в моделировании экономических процессов не рассматривается. Вместе с тем, интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике.

Определение интегральной суммы позволяет использовать понятие определенного интеграла в социально-экономической сфере. Его применение основано на том, что любой меняющийся социально-экономический процесс может быть интерпретирован как скачкообразный, скачки которого близки к нулю.

Потребительский излишек

Остановимся на нескольких примерах использования интегрального исчисления в экономике. Начнем с широко используемого в рыночной экономике понятия потребительского излишка (CS–consumer’s surplus). Для этого введем несколько экономических понятий и обозначений.

Спрос на данный товар (D–demand) – сложившаяся на определенный момент времени зависимость между ценой товара и объемом его покупки. Спрос на отдельный товар графически изображается в виде кривой с отрицательным наклоном, отражающей взаимосвязь между ценой P (price) единицы этого товара и количеством товара Q (quantity), которое потребители готовы купить при каждой заданной цене. Отрицательный наклон кривой спроса имеет очевидное объяснение: чем дороже товар, тем меньше количество товара, которое покупатели готовы купить, и наоборот.

Аналогично определяется и другое ключевое понятие экономической теории – предложение (S–supply) товара: сложившаяся на определенный момент времени зависимость между ценой товара и количеством товара, предлагаемого к продаже. Предложение отдельного товара изображается графически в виде кривой с положительным наклоном, отражающей взаимосвязь между ценой единицы этого товара P и количеством товара Q, которое потребители готовы продать при каждой цене.

Отметим, что экономисты сочли удобным изображать аргумент (цену) по оси ординат, а зависимую переменную (количество товара) по оси абсцисс. Поэтому графики функций спроса и предложения выглядят следующим образом

И, наконец, введем еще одно понятие, играющее большую роль в моделировании экономических процессов – рыночное равновесие (equilibrium). Состояние равновесия характеризуют такие цена и количество, при которых объем спроса совпадает с величиной предложения, а графически рыночное равновесие изображается точкой пересечения кривых спроса и предложения (рис. 2.2), E*(p*; q*) – точка равновесия.

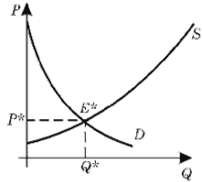
Рис.2.2 Точка рыночного равновесия

В дальнейшем для удобства анализа мы будем рассматривать не зависимость Q = f(P), а обратные функции спроса и предложения, характеризующие зависимость P = f(Q), тогда аргумент и значение функции графически будут изображаться привычным для нас образом.

Перейдем теперь к рассмотрению приложений интегрального анализа для определения потребительского излишка [5]. Для этого изобразим на графике обратную функцию спроса P = f(Q). Допустим, что рыночное равновесие установилось в точке E*(q*; p*) (кривая предложения на графике отсутствует для удобства дальнейшего анализа, рис.2.3).

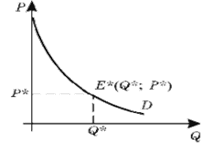
Рис.2.3. График рыночного равновесия

Если покупатель приобретает товар в количестве Q* по равновесной цене P*, то очевидно, что общие расходы на покупку такого товара составят P*Q*, что равно площади заштрихованной фигуры A (рис.2.4).

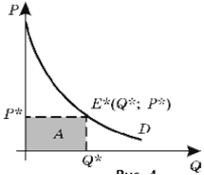
Рис.2.4. Общие расходы на покупку товара

Но предположим теперь, что товар в количестве Q* продается продавцами не сразу, а поступает на рынок небольшими партиями Q. Именно такое допущение вместе с предположением о непрерывности функции спроса и предложения является основным при выводе формулы для расчета потребительского излишка (см. [2.1–2.4]). Отметим, что данное допущение вполне оправдано, потому что такая схема реализации товара довольно распространена на практике и вытекает из цели продавца поддерживать цену на товар как можно выше. определенный интеграл экономический смысл

Тогда получим, что сначала предлагается товар в количестве Q1 = D Q (рис.2.5), который продается по цене P1 = f(Q1). Так как по предположению величина Q мала, то можно считать, что вся первая партия товара реализуется по цене P1, при этом затраты покупателя на покупку такого количества товара составят P1D Q, что соответствует площади заштрихованного прямоугольника S1 (рис.2.5) [5].

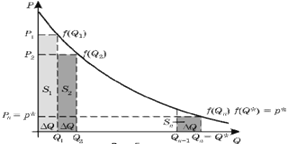
Рис.2.5. Затраты покупателя

Далее на рынок поступает вторая партия товара в том же количестве, которая продается по цене P2 = f(Q2), где Q2 = Q1 + D Q – общее количество реализованной продукции, а затраты покупателя на покупку второй партии составят P2D Q, что соответствует площади прямоугольника S2.

Продолжим процесс до тех пор, пока не дойдем до равновесного количества товара Q* = Qn. Тогда становится ясно, какой должна быть величина DQ для того, чтобы процесс продажи товара закончился в точке Q*:

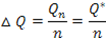
В результате получим, что цена n-й партии товара Pn = f(Qn) = f(Q*) = P*, а затраты потребителей на покупку этой последней партии товара составят PnD Q, или площадь прямоугольника Sn.

Таким образом, мы получим, что суммарные затраты потребителей при покупке товара мелкими партиями D Q равны:

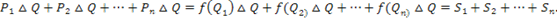
Так как величина D Q очень мала, а функция f(Q) непрерывна, то заключаем, что 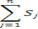приблизительно равна площади фигуры B (рис.2.6) [5].

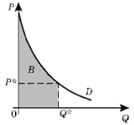
Рис.2.6. Суммарные затраты потребителей

Площадь фигуры B при малых приращениях аргумента D Q равна определенному интегралу от обратной функции спроса при изменении аргумента от 0 до Q*, т. е. в итоге получим, что:

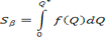(2.1)

Вспомнив, что каждая точка на кривой спроса Pi = f(Qi) (i = 1, 2, ..., k) показывает, какую сумму потребитель готов заплатить за покупку дополнительной единицы продукта, получим, что площадь фигуры B соответствует общей денежной сумме, которую потребитель готов потратить на покупку Q* единиц товара. Разность между площадью фигуры B и площадью прямоугольника A есть потребительский излишек при покупке данного товара – превышение общей стоимости, которую потребитель готов уплатить за все единицы товара, над его реальными расходами на их приобретение (площадь заштрихованной фигуры на рисунке 2.7).

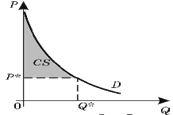
Рис.2.7. Потребительский излишек

Таким образом, потребительский излишек можно посчитать по следующей формуле:

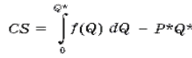, (2.2)