Численные методы вычисления определенного интеграла. Формулы прямоугольников и трапеций. Формула Симсона для вычисления неопределенных интегралов.

В настоящее время известно много формул приближенного интегрирования, называемых также квадратурными формулами (формулы вычисления площадей).

Формула прямоугольников. Вывод этой формулы основан на замене определенного интеграла интегральной суммой. Из анализа известно, что

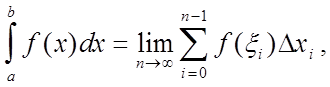
где 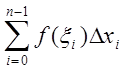- интегральная сумма для функции f(x) на отрезке [a, b].

ξ – внутренняя точка отрезка [a, b].

Если отрезок [a, b] разбить на n равных частей:

а=х₀ , х₁ , …, х_п=b,

то

∆х_i = = h.

Число h называется шагом квадратурной формулы. При этом условии получаем:

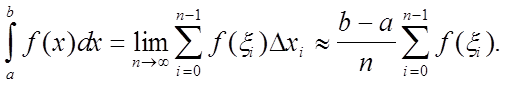
Если взять в качестве точек ξ_i левые концы частичных отрезков:

f(ξ_i) = f(х_i) (i = 0, 1, …, n-1),

то

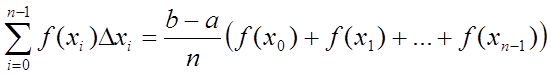
Обозначим f(х_i) = у_i. Заменяя интеграл интегральной суммой, получим приближенное равенство:

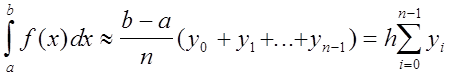, (2)

называемое формулой прямоугольников (с левыми ординатами).

Если взять в качестве точек ξ_i правые концы частичных отрезков:

f(ξ_i) =f(х_i) (i = 1, 2,…, n),

то получим приближенное равенство:

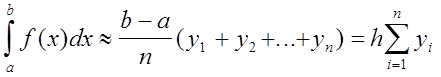, (3)

называемое формулой прямоугольников (с правыми ординатами).

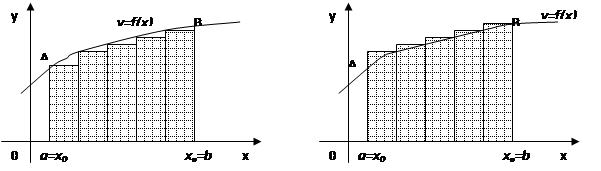
Геометрический смысл формулы прямоугольников состоит в том, что криволинейная трапеция заменяется ступенчатой фигурой, составленной из прямоугольников. Приближенное значение интеграла равно площади ступенчатой фигуры.

Пример. Вычислим интеграл 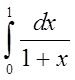, разбив интервал интегрирования на 10 равных частей (n = 10). Найдем и запишем в таблицу значения подынтегральной функции

у = в точках деления:

i	хi	уi =	i	хi	уi =
	0,0	1,00000		0,6	0,62500
	0,1	0,90909		0,7	0,58824
	0,2	0,83333		0,8	0,55556
	0,3	0,76923		0,9	0,52632
	0,4	0,71429		1,0	0,50000
	0,5	0,66667

По формуле прямоугольников с левыми ординатами получим:

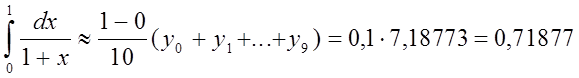
По формуле прямоугольников с правыми ординатами получим:

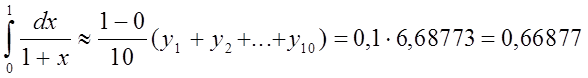
Значение, полученное по формуле (1):

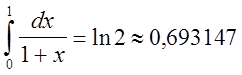
Мы видим, что формулы прямоугольников дают грубые приближения.

Так как функция у = является убывающей на отрезке
[0; 1], то формула прямоугольников с левыми ординатами позволяет получить приближенное значение интеграла с избытком, формула прямоугольников с правыми ординатами – с недостатком.

Абсолютную погрешность r формул прямоугольников (2) и (3) можно оценить по формуле:

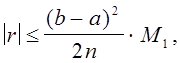(4)

где

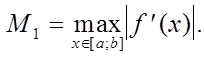
Идея вывода квадратурных формул трапеций и Симпсона:

подынтегральной функции f(x) поставить в соответствие близкую ей функцию g_n(x), которую можно проинтегрировать, и приближенно заменить искомый интеграл Iинтегралом от этой функции.

Формула трапеций.Пусть требуется вычислить интеграл

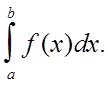
Обозначим a = x₀ , b = x₁.

В качестве аппроксимирующей функции g(x) выберем линейную функцию и произведем замену подынтегральной функции f(x) по формуле линейного интерполирования

f(x) ≈ у₀ + tDу₀ ,

где

у₀ =f(x₀) , у₁ =f(x₁), Dу₀ = у₁- у₀.

В этом случае

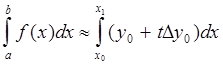, (5)

Известно, что t =

Отсюда х=х₀ +th и dx =hdt.

При х = х₀ t = 0;

при х =х₁ t = 1.

Переходя к новой переменной t, получим:

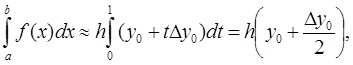
или

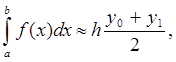(6)

так как Dу₀ =у₁ –у₀

Формула (6) называется формулой трапеций.

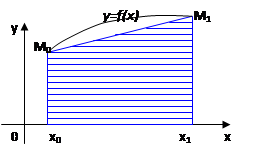
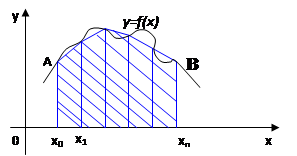
Ее геометрический смысл состоит в том, что на отрезке
[х₀; х₁] кривая у = f(х) заменяется отрезком прямой (хордой), т. е. криволинейная трапеция заменяется прямолинейной.

Значение интеграла, вычисленное по формуле (6), будет равно площади трапеции. На рисунке эта площадь заштрихована.

Как показывает вычислительная практика, при недостаточно малой длине отрезка интегрирования точность результатов, полученных с помощью формулы (6), бывает недостаточной.

Для получения более точного результата поступают следующим образом:

Отрезок интегрирования [а;b] разбивают на п равных частей точками: х₀ = а, х₁ , х₂ ,…,х_n =b. И аппроксимируют кусочно-линейной функцией g_п(x). Применяя формулу (6) на каждом из частичных отрезков интегрирования, получают:

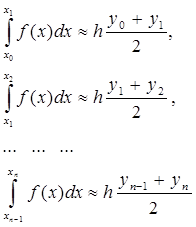(7)

Сложив равенства, получают формулу, называемую обобщенной формулой трапеций:

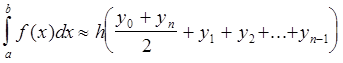(8)

где у_i =f(х_i ) (i = 0, 1, …, n).

Геометрический смысл этой формулы состоит в том, что кривая — график функции у = f(х) — заменяется ломаной, вписанной в кривую АВ. Площадь криволинейной трапеции заменяется суммой площадей прямолинейных трапеций. Как показывает практика, формула (8) при большом числе точек деления позволяет получать хорошие результаты.

Пример 1. Вычислим по формуле трапеций (8) интеграл 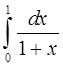, разбив отрезок интегрирования на десять равных частей.

Воспользовавшись данными, занесенными в предыдущую таблицу, получим:

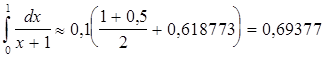
Сравнение полученного результата со значением ln2 » 0,693147 показывает, что погрешность значения интеграла, вычисленного по обобщенной формуле трапеций, значительно меньше погрешности, допущенной при вычислении этого же интеграла по формуле прямоугольников.

Можно показать, что погрешность результатов, получаемых по обобщенной формуле трапеций, подсчитывается по формуле

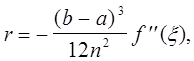(9)

где а < x < b,

а абсолютная погрешность оценивается следующим образом:

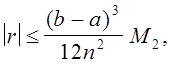(10)

где

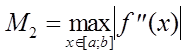(11)