Первообразная функции. Теорема о существовании первообразной функции.
Первообразная функции. Теорема о существовании первообразной функции.
Пусть на промежутке  определены функции
определены функции  и
и  , и во всех точках этого промежутка имеет место равенство
, и во всех точках этого промежутка имеет место равенство
 |
Тогда говорят, что функция  есть первообразная функция, или просто первообразная функции
есть первообразная функция, или просто первообразная функции  на промежутке
на промежутке  .
.
Теорема. («Единственность» первообразной). Если  –
–
одна из первообразных функций для функции  на промежутке
на промежутке  , то любая первообразная
, то любая первообразная 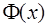 функции
функции  на промежутке
на промежутке  имеет вид
имеет вид  , где
, где  - некоторая постоянная на промежутке
- некоторая постоянная на промежутке  функция.
функция.
Доказательство. Введём функцию  Функция
Функция  дифференцируема на промежутке
дифференцируема на промежутке  как разность двух дифференцируемых функций, причём, всюду на
как разность двух дифференцируемых функций, причём, всюду на 


Тогда в силу следствия из теоремы Лагранжа функция  постоянна на промежутке
постоянна на промежутке  , т.е.
, т.е.  , или
, или  , что и требовалось доказать.
, что и требовалось доказать.
Итак, если  - первообразная функции
- первообразная функции  на промежутке
на промежутке  , то множество всех её первообразных совпадает с множеством
, то множество всех её первообразных совпадает с множеством  , где
, где  - произвольная постоянная на промежутке
- произвольная постоянная на промежутке  функция.
функция. 
Итак, первообразная данной функции на данном промежутке единственна с точностью до постоянного слагаемого.
Методы нахождения неопределенных интегралов. Непосредственное интегрирование.
Интегрирование, основанное на прямом использовании таблицы интегралов и свойств неопределенного интеграла, называется непосредственным интегрированием.
При непосредственном интегрировании могут представиться три случая.
I. Интеграл находят непосредственно по соответствующему табличному интегралу.
Примеры
1)  ;
;
2)  ;
;
II. Интеграл приводится к одному или нескольким табличным интегралам в результате применения свойств неопределенного интеграла.
Примеры
1. 
 ;
;
2. 
 .
.
III. Интеграл приводится к одному или нескольким табличным интегралам в результате элементарных тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Примеры
1. 
 ;
;
2.  ;
;
Интегрирование некоторых функций, содержащих квадратный трехчлен в знаменателе
Рассмотрим интегралы вида  . Они с помощью замены
. Они с помощью замены  приводятся к известным интегралам.
приводятся к известным интегралам.
Пример 1. 


 .
.
Замечание 1. Если для первого из рассмотренных интегралов квадрат-ный трёхчлен имеет действительные корни, то более целесообразно преобразовать подынтегральную функцию, представив её как сумму алгебраических дробей со знаменателями–множителями в разложении квадратного трёхчлена. Более подробно об этом будет рассмотрено в следующей лекции.
Пример 2. Найти интеграл  .
.
Преобразуем подынтегральную функцию:
 .
.
Определим коэффициенты А и В, выполнив сложение дробей и приравняв числители дробей правой и левой частей равенства:
 .
.
Приравнивая коэффициенты при х и свободные члены, получим

откуда  .
.
Тогда имеем

Дифференциал уравнения. Основные понятия. Нахождение уравнения по его решению
Дифференциальным уравнением называется уравнение, связывающее независимую переменную 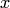 , искомую функцию
, искомую функцию 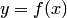 и её производные
и её производные 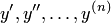 , т. е. уравнение вида
, т. е. уравнение вида
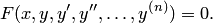
Если искомая функция 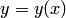 есть функция одной независимой переменной
есть функция одной независимой переменной 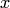 , дифференциальное уравнение называется обыкновенным.
, дифференциальное уравнение называется обыкновенным.
Когда искомая функция 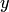 есть функция двух и более независимых переменных, например, если
есть функция двух и более независимых переменных, например, если 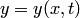 , то уравнение вида
, то уравнение вида
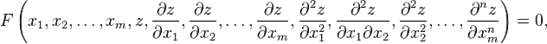
называется уравнением в частных производных. Здесь 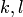 — неотрицательные целые числа, такие, что
— неотрицательные целые числа, такие, что 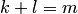 .
.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение 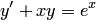 — уравнение первого порядка, дифференциальное уравнение
— уравнение первого порядка, дифференциальное уравнение 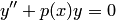 , где
, где 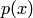 — известная функция, — уравнение второго порядка; дифференциальное уравнение
— известная функция, — уравнение второго порядка; дифференциальное уравнение 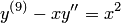 — уравнение 9-го порядка.
— уравнение 9-го порядка.
Решением дифференциального уравнения n-го порядка на интервале 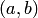 называется функция
называется функция 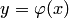 , определенная на интервале
, определенная на интервале 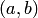 вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции
вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции 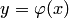 в дифференциальное уравнение превращает последнее в тождество по
в дифференциальное уравнение превращает последнее в тождество по 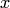 на
на 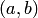 . Например, функция
. Например, функция 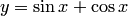 является решением уравнения
является решением уравнения 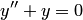 на интервале
на интервале 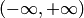 . В самом деле, дифференцируя функцию дважды, будем иметь
. В самом деле, дифференцируя функцию дважды, будем иметь
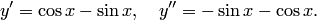
Подставляя выражения 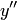 и
и 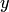 в дифференциальное уравнение, получим тождество
в дифференциальное уравнение, получим тождество
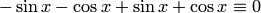
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Задача Коши.
 |
Пусть
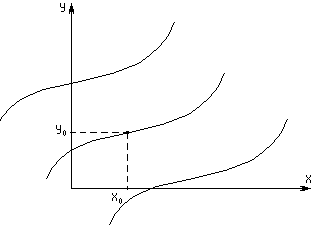
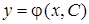 будет общим решением уравнения (2). Это общее решение определяет семейство интегральных кривых. Для того чтобы из этого семейства выделить какое-либо частное решение, необходимо задать еще дополнительные условия, в частности, частное решение можно выделить путем задания на плоскости точки
будет общим решением уравнения (2). Это общее решение определяет семейство интегральных кривых. Для того чтобы из этого семейства выделить какое-либо частное решение, необходимо задать еще дополнительные условия, в частности, частное решение можно выделить путем задания на плоскости точки 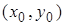 , через которую проходит интересующая нас интегральная кривая. Следовательно, возникает задача отыскания такого решения уравнения
, через которую проходит интересующая нас интегральная кривая. Следовательно, возникает задача отыскания такого решения уравнения 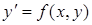 , которое при заданном
, которое при заданном 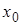 принимает заданное значение
принимает заданное значение 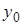 .
.Это записывают так: 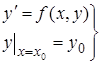 (4)
(4)
Такая задача называется задачей Коши.
Условие 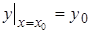 называется начальным условием. Начальные условия необходимы для определения соответствующего значения произвольной постоянной С. Покажем на примере как вычисляется С.
называется начальным условием. Начальные условия необходимы для определения соответствующего значения произвольной постоянной С. Покажем на примере как вычисляется С.
Пусть требуется среди решений уравнения 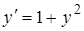 (5)
(5)
найти такое, которое при 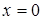 обращается в нуль, т.е.
обращается в нуль, т.е. 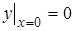 . (6)
. (6)
Общим решением служит функция 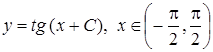 (7)
(7)
Так как требуется, чтобы выполнялось (6), то должно быть 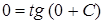 , а это возможно только при
, а это возможно только при 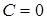 . Следовательно, частное решение, удовлетворяющее условию (6), получается из общего решения при
. Следовательно, частное решение, удовлетворяющее условию (6), получается из общего решения при 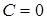 , т.е.
, т.е. 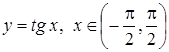 . Это и есть решение задачи Коши.
. Это и есть решение задачи Коши.
Основное свойство общего решения:
Общее решение 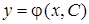 дифференциального уравнения
дифференциального уравнения 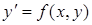 обладает тем свойством, что из него по любому заданному допустимому начальному условию
обладает тем свойством, что из него по любому заданному допустимому начальному условию 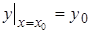 может быть найдено частное решение, удовлетворяющее этому условию. Это означает, что подставив в общее решение
может быть найдено частное решение, удовлетворяющее этому условию. Это означает, что подставив в общее решение 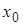 вместо
вместо 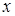 и
и 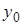 вместо
вместо 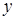 , получаем уравнение относительно С:
, получаем уравнение относительно С: 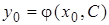 , из которого всегда может быть найдено значение
, из которого всегда может быть найдено значение 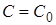 и притом единственное. Функция
и притом единственное. Функция 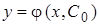 служит искомым частным решением.
служит искомым частным решением.
Замечания:
1. Сформулированное основное свойство общего решения справедливо при определенных требованиях, наложенных на функцию 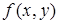 . Эти требования даются теоремой существования и единственности.
. Эти требования даются теоремой существования и единственности.
2. Допустимыми начальными условиями 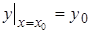 называются такие условия, когда точка
называются такие условия, когда точка 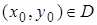 , где D – область определения функции
, где D – область определения функции 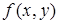 .
.
3. Пусть 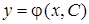 будет общим решением некоторого дифференциального уравнения.
будет общим решением некоторого дифференциального уравнения.
Условие Липшица
Рассмотрим функцию 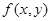 , определенную и непрерывную в прямоугольнике К:
, определенную и непрерывную в прямоугольнике К: 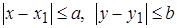
Определение. Если для любого 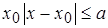 и любых двух значений
и любых двух значений 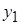 и
и 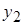 переменной
переменной 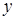 :
:
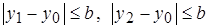 , существует такое, не зависящее от х число
, существует такое, не зависящее от х число 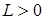 , что выполнено неравенство:
, что выполнено неравенство: 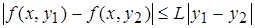 (1), то говорят, что функция
(1), то говорят, что функция 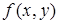 в области К удовлетворяет условию Липшица с постоянной L.
в области К удовлетворяет условию Липшица с постоянной L.
Замечания:
1. Если 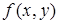 в области К имеет непрерывную частную производную
в области К имеет непрерывную частную производную 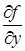 , то всегда найдется такое L, что условие (1) будет выполнено. Действительно, тогда по формуле Лагранжа
, то всегда найдется такое L, что условие (1) будет выполнено. Действительно, тогда по формуле Лагранжа 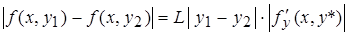 (2),
(2),
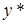 – лежит между
– лежит между 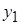 и
и 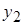 .
.
В силу непрерывности 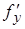 в К и замкнутости области К,
в К и замкнутости области К, 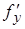 в К ограничена, т.е.
в К ограничена, т.е. 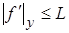 , где L – некоторая константа. В этом случае, в частности, за L можно принять
, где L – некоторая константа. В этом случае, в частности, за L можно принять 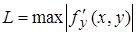 .
.
2. Условие Липшица (1) более слабое, чем существование частной производной 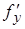 , так как оно может быть выполнено и в том случае, когда
, так как оно может быть выполнено и в том случае, когда 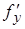 существует не всюду в К.
существует не всюду в К.
Однородные уравнения.
Определение. Уравнение 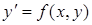 (1) называется однородным, если
(1) называется однородным, если 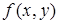 может быть представлена как функция отношения своих аргументов, т.е.
может быть представлена как функция отношения своих аргументов, т.е. 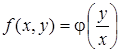 (2)
(2)
Таким образом, однородное уравнение имеет вид: 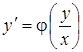 (3)
(3)
Теорема. Однородное уравнение (3) имеет общий интеграл: 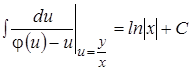 . (4)
. (4)
Замечание 1. В доказательстве теоремы мы предполагаем, что 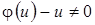 . Рассмотрим тот случай, когда
. Рассмотрим тот случай, когда 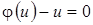 . Здесь имеются две возможности.
. Здесь имеются две возможности.
а) 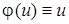 Тогда
Тогда 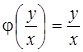 и уравнение (3) принимает вид:
и уравнение (3) принимает вид: 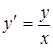 .
.
Это уравнение с разделяющимися переменными 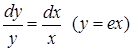 и здесь никаких преобразований делать не нужно.
и здесь никаких преобразований делать не нужно.
б) уравнение 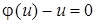 удовлетворяется лишь при определенных значениях
удовлетворяется лишь при определенных значениях 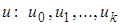 . В этом случае могут быть потеряны решения
. В этом случае могут быть потеряны решения 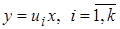 . Интегральные кривые суть прямые, проходящие через начало.
. Интегральные кривые суть прямые, проходящие через начало.
Пример. Решить уравнение 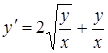 .
.
Решение. Уравнение однородное. Полагаем 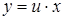 .
. 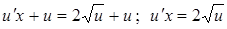 .
.
Если 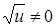 , то
, то 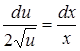 . Отсюда
. Отсюда 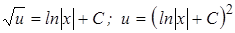 .
.
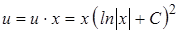 – общий интеграл.
– общий интеграл.
Может быть потеряно решение 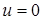 или
или 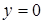 .
.
Действительно, 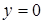 есть решение рассматриваемого уравнения и оно не может быть получено из общего интеграла ни при каком значении С, следовательно
есть решение рассматриваемого уравнения и оно не может быть получено из общего интеграла ни при каком значении С, следовательно 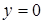 есть особое решение.
есть особое решение.
Замечание 2. Формулу (4) запоминать не следует. Надо уметь ее выводить в каждом конкретном случае, как это сделано в примере.
Замечание 3. Для интегрирования уравнения более общего вида, чем (3) 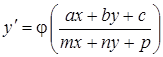 . (6)
. (6)
(обобщенное однородное) сначала делают замену неизвестной функции и независимой переменной по формулам 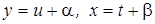 ; выбирая
; выбирая 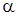 и
и 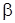 такими, чтобы исчезли свободные члены в числителе и знаменателе аргумента
такими, чтобы исчезли свободные члены в числителе и знаменателе аргумента 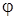 в (6), тогда (6) приводится к однородному уравнению.
в (6), тогда (6) приводится к однородному уравнению.
Определение интегральной суммы позволяет использовать понятие определенного интеграла в социально-экономической сфере. Его применение основано на том, что любой меняющийся социально-экономический процесс может быть интерпретирован как скачкообразный, скачки которого близки к нулю.
Потребительский излишек
Остановимся на нескольких примерах использования интегрального исчисления в экономике. Начнем с широко используемого в рыночной экономике понятия потребительского излишка (CS–consumer’s surplus). Для этого введем несколько экономических понятий и обозначений.
Спрос на данный товар (D–demand) – сложившаяся на определенный момент времени зависимость между ценой товара и объемом его покупки. Спрос на отдельный товар графически изображается в виде кривой с отрицательным наклоном, отражающей взаимосвязь между ценой P (price) единицы этого товара и количеством товара Q (quantity), которое потребители готовы купить при каждой заданной цене. Отрицательный наклон кривой спроса имеет очевидное объяснение: чем дороже товар, тем меньше количество товара, которое покупатели готовы купить, и наоборот.
Аналогично определяется и другое ключевое понятие экономической теории – предложение (S–supply) товара: сложившаяся на определенный момент времени зависимость между ценой товара и количеством товара, предлагаемого к продаже. Предложение отдельного товара изображается графически в виде кривой с положительным наклоном, отражающей взаимосвязь между ценой единицы этого товара P и количеством товара Q, которое потребители готовы продать при каждой цене.
Отметим, что экономисты сочли удобным изображать аргумент (цену) по оси ординат, а зависимую переменную (количество товара) по оси абсцисс. Поэтому графики функций спроса и предложения выглядят следующим образом
И, наконец, введем еще одно понятие, играющее большую роль в моделировании экономических процессов – рыночное равновесие (equilibrium). Состояние равновесия характеризуют такие цена и количество, при которых объем спроса совпадает с величиной предложения, а графически рыночное равновесие изображается точкой пересечения кривых спроса и предложения (рис. 2.2), E*(p*; q*) – точка равновесия.
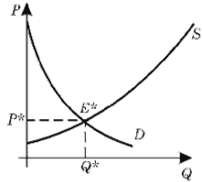
Рис.2.2 Точка рыночного равновесия
В дальнейшем для удобства анализа мы будем рассматривать не зависимость Q = f(P), а обратные функции спроса и предложения, характеризующие зависимость P = f(Q), тогда аргумент и значение функции графически будут изображаться привычным для нас образом.
Перейдем теперь к рассмотрению приложений интегрального анализа для определения потребительского излишка [5]. Для этого изобразим на графике обратную функцию спроса P = f(Q). Допустим, что рыночное равновесие установилось в точке E*(q*; p*) (кривая предложения на графике отсутствует для удобства дальнейшего анализа, рис.2.3).
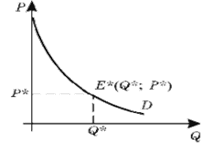
Рис.2.3. График рыночного равновесия
Если покупатель приобретает товар в количестве Q* по равновесной цене P*, то очевидно, что общие расходы на покупку такого товара составят P*Q*, что равно площади заштрихованной фигуры A (рис.2.4).
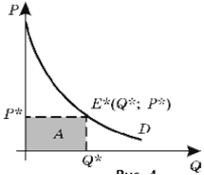
Рис.2.4. Общие расходы на покупку товара
Но предположим теперь, что товар в количестве Q* продается продавцами не сразу, а поступает на рынок небольшими партиями Q. Именно такое допущение вместе с предположением о непрерывности функции спроса и предложения является основным при выводе формулы для расчета потребительского излишка (см. [2.1–2.4]). Отметим, что данное допущение вполне оправдано, потому что такая схема реализации товара довольно распространена на практике и вытекает из цели продавца поддерживать цену на товар как можно выше. определенный интеграл экономический смысл
Тогда получим, что сначала предлагается товар в количестве Q1 = D Q (рис.2.5), который продается по цене P1 = f(Q1). Так как по предположению величина Q мала, то можно считать, что вся первая партия товара реализуется по цене P1, при этом затраты покупателя на покупку такого количества товара составят P1D Q, что соответствует площади заштрихованного прямоугольника S1 (рис.2.5) [5].
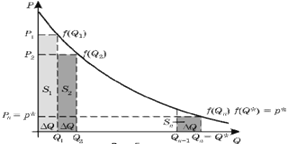
Рис.2.5. Затраты покупателя
Далее на рынок поступает вторая партия товара в том же количестве, которая продается по цене P2 = f(Q2), где Q2 = Q1 + D Q – общее количество реализованной продукции, а затраты покупателя на покупку второй партии составят P2D Q, что соответствует площади прямоугольника S2.
Продолжим процесс до тех пор, пока не дойдем до равновесного количества товара Q* = Qn. Тогда становится ясно, какой должна быть величина DQ для того, чтобы процесс продажи товара закончился в точке Q*:
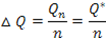
В результате получим, что цена n-й партии товара Pn = f(Qn) = f(Q*) = P*, а затраты потребителей на покупку этой последней партии товара составят PnD Q, или площадь прямоугольника Sn.
Таким образом, мы получим, что суммарные затраты потребителей при покупке товара мелкими партиями D Q равны:
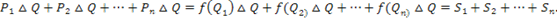
Так как величина D Q очень мала, а функция f(Q) непрерывна, то заключаем, что 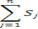 приблизительно равна площади фигуры B (рис.2.6) [5].
приблизительно равна площади фигуры B (рис.2.6) [5].
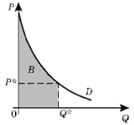
Рис.2.6. Суммарные затраты потребителей
Площадь фигуры B при малых приращениях аргумента D Q равна определенному интегралу от обратной функции спроса при изменении аргумента от 0 до Q*, т. е. в итоге получим, что:
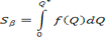 (2.1)
(2.1)
Вспомнив, что каждая точка на кривой спроса Pi = f(Qi) (i = 1, 2, ..., k) показывает, какую сумму потребитель готов заплатить за покупку дополнительной единицы продукта, получим, что площадь фигуры B соответствует общей денежной сумме, которую потребитель готов потратить на покупку Q* единиц товара. Разность между площадью фигуры B и площадью прямоугольника A есть потребительский излишек при покупке данного товара – превышение общей стоимости, которую потребитель готов уплатить за все единицы товара, над его реальными расходами на их приобретение (площадь заштрихованной фигуры на рисунке 2.7).
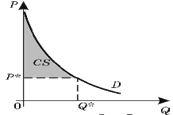
Рис.2.7. Потребительский излишек
Таким образом, потребительский излишек можно посчитать по следующей формуле:
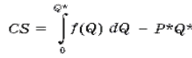 , (2.2)
, (2.2)
Аналогично,
 (2.3)
(2.3)
Где С(q) – функция издержек
MC – предельные издержки;
T – время .
Действительно, С(1)=С0, так что поставленное начальное условие выполнено. Кроме того, мы знаем, что для непрерывных функций MC(t) интеграл справа в уравнении (2.4) есть дифференцируемая функция, производная которой в точке q равна MC(q). Стало быть, этот интеграл действительно выражает искомую функцию издержек [4].
Как известно, дисконтирование представляет собой специальный приём для сопоставления текущей и будущей (очевидно, более низкой, чем текущая) ценности денежных сумм. Дисконтирование также называют снижение ценности отсроченных денежных поступлений.
Пусть в дискретные моменты времени t = 1, 2, 3, … . величина денежных поступлений составляет R(1), R(2), R(3), … . Если ставку банковского процента, соответствующую одному временному такту обозначит через р, то, пересчитывая эти значения на настоящий момент и складывая результаты, получим дисконтированную стоимость всего потока, соответствующего изменению времени от 1до n:
 (2.5)
(2.5)
 Величина П, меньшая, чем сумма , дает теперешнюю суммарную стоимость всех поступлений за указанный период времени [4].
Величина П, меньшая, чем сумма , дает теперешнюю суммарную стоимость всех поступлений за указанный период времени [4].
Рассмотрим теперь модель с непрерывным временем, изменяющимся на некотором отрезке [0,T]. В такой модели как сами выплаты, так и снижение их ценности происходят непрерывно. Если в момент времени t выплачиваемые средства составляют R(t) условных единиц, то в качестве характеристики изменения денежного потока целесообразно взять производную функции R(t) по времени:  которую именуют скоростью денежного потока. Ясно, что мы имеем теперь дело не с дискретными значениями потока, а с его приращениями (их приближенно заменим дифференциалами функции R(t) dR(t;dt) = I(t)dt за время от t до t + dt.
которую именуют скоростью денежного потока. Ясно, что мы имеем теперь дело не с дискретными значениями потока, а с его приращениями (их приближенно заменим дифференциалами функции R(t) dR(t;dt) = I(t)dt за время от t до t + dt.
Для нахождения дисконтированной стоимости dП такого приращения разобьем единичный временной промежуток на k равных частей. Тогда отрезок [0;t], в конце которого за время dt поток прирастает на dR(t;dt), разобьётся на kt равных частей [4]. Далее осуществим в формуле (2.4) переход к пределу при k→∞, взяв в знаменателе ее правой части в качестве коэффициента дисконтирования величину  , а в числителе - приращение dR(t;dt):
, а в числителе - приращение dR(t;dt):

T – время .
Где U – количесво денег
f(t) – количество денег;
T – время .
т. е. если f(t) - количество денег, поступивших в банк в момент времени t, то  есть общее количество денег, поступивших в банк за промежуток времени [0, Т].
есть общее количество денег, поступивших в банк за промежуток времени [0, Т].
Поскольку f(t)≥0, то общее количество денег, поступивших в Сбербанк за промежуток времени [0, Т] численно равно площади фигуры под графиком функции f(t) [4].
Где Q – обьем продукции
f(t) – производительност труда в момент времени t;
T – время.
Поскольку f(t)≥0, то объем продукции, произведенной за промежуток времени [О, Т], численно равен площади фигуры под графиком функции f(t), описывающей изменение производительности труда с течением времени, на промежутке [О, Т] [5].
Возможность учета влияния различных факторов на изменение производительности производства связана с использованием, например, так называемых функций Кобба-Дугласа. В этом случае производительность f(t) представляется в виде произведения трех сомножителей :
F(t) = α0Aa (t)LβKγ(t), (2.9)
Рис.2.8. Кривая Лоренца
выражает график зависимости процента доходов от процента, имеющего их населения. По оси Оу откладывается доля населения, имеющих определенный доход; по оси Ох долю населения [4]. С помощью кривой Лоренца можно оценить степень неравенства в распределении доходов населения. При равномерном распределении доходов кривая Лоренца является линейной функцией - биссектрисой ОA, при неравномерном - кривой вида ОBА. Коэффициентом Джини именуют отношение площади фигуры между биссектрисой ОЛ и кривой Лоренца к площади треугольника ОАС.
k =  (2.10)
(2.10)
Где k – коэффициент Джини
SOAB – площадь фигуры ОАВ;
SOAC – gkjoflm abuehs OAC.
При коэффициенте, равном 0, налицо полное равенство в доходах населения, при значении коэффициента менее 0,3 - слабое неравенство, при 0,3-0,7 - значительное, при 0,7-1 – сильное [4].
Первообразная функции. Теорема о существовании первообразной функции.
Пусть на промежутке  определены функции
определены функции  и
и  , и во всех точках этого промежутка имеет место равенство
, и во всех точках этого промежутка имеет место равенство
 |
Тогда говорят, что функция  есть первообразная функция, или просто первообразная функции
есть первообразная функция, или просто первообразная функции  на промежутке
на промежутке  .
.
Теорема. («Единственность» первообразной). Если  –
–
одна из первообразных функций для функции  на промежутке
на промежутке  , то любая первообразная
, то любая первообразная 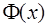 функции
функции  на промежутке
на промежутке  имеет вид
имеет вид  , где
, где  - некоторая постоянная на промежутке
- некоторая постоянная на промежутке  функция.
функция.
Доказательство. Введём функцию  Функция
Функция  дифференцируема на промежутке
дифференцируема на промежутке  как разность двух дифференцируемых функций, причём, всюду на
как разность двух дифференцируемых функций, причём, всюду на 


Тогда в силу следствия из теоремы Лагранжа функция  постоянна на промежутке
постоянна на промежутке  , т.е.
, т.е.  , или
, или  , что и требовалось доказать.
, что и требовалось доказать.
Итак, если  - первообразная функции
- первообразная функции  на промежутке
на промежутке  , то множество всех её первообразных совпадает с множеством
, то множество всех её первообразных совпадает с множеством  , где
, где  - произвольная постоянная на промежутке
- произвольная постоянная на промежутке  функция.
функция. 
Итак, первообразная данной функции на данном промежутке единственна с точностью до постоянного слагаемого.
