Действие магнитного поля на контур с током

Выясним, как ведет себя контур с током в однородном магнитном поле . Согласно (1.5) на каждый элемент контура действует сила

.

Результирующая этих сил

.

Вынеся постоянные величины 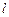и за знак интеграла, получим:

.

Интеграл , поэтому . Таким образом, результирующая сила, действующая на контур с током в однородном магнитном поле, равна нулю. Это справедливо для контуров любой формы (в том числе неплоских) при произвольном расположении контура относительно направления . Существенной для равенства нулю результирующей силы является лишь однородность поля.

Предположим, что контур имеет прямоугольную форму. Рассмотрим два случая.

1) Пусть перпендикулярен , т.е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, показаны на рис. 1.14, а.

Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжатии и растяжении и контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.

2) Пусть параллелен 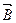, т.е. нормаль плоскости контура перпендикулярна вектору магнитной индукции (рис.1,14, б).

,

тогда силы Ампера на каждом участке, определяются следующим образом:

I. , , сила направлена от нас;

II, IV. , , т.е. на элемент контура с током, лежащим вдоль силовых линий, не действует;

III. , , сила направлена к нам.

Если контур с током закрепить в точках 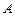и , то при таком расположении его в магнитном поле он будет вращаться, т.е. на него будет действовать момент силы .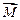

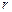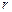Пусть – плечо силы (рис. 1.14, б). Если перпендикулярна , тогда и момент силы, действующий на I (или III) участок контура

,

где – площадь между линией AD и участком тока I (или III).

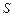Поскольку на каждую из противоположных сторон контура (участки I и III) действует самостоятельная сила Ампера, то в качестве площади для суммарного момента сил принимается не половина площади контура, а вся. Тогда понятие магнитного момента контура с током вводится как собственная характеристика контура, которая численно равна , где – площадь контура. Направление магнитного момента задается нормалью контура с током .

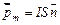Полный момент силы, действующий на контур с током в магнитном поле, численно равен: .

Модуль вектора 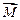равен: .

Для того чтобы угол 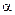между векторам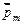и и 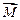увеличить на , нужно совершить против сил, действующих на контур в магнитном поле, работу

. (1.16)

Возвращаясь в первоначальное положение, контур может вернуть затраченную на его поворот работу, совершив ее над каким-нибудь телом. Следовательно, работа (1.16) идет на увеличение потенциальной энергии , которой обладает контур с током в магнитном поле:

.

Интегрируя, находим:

,

полагая , получаем:

.

Параллельная ориентация векторов 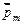и 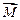отвечает минимуму энергии и, следовательно, положению устойчивого равновесия контура.

Магнитное поле в веществе

Магнитомеханические явления

До сих пор мы рассматривали магнитное поле в вакууме. Если проводники с током находятся не в вакууме, а в другой среде, то магнитное поле изменяется.

Различные вещества в магнитном поле намагничиваются, т.е. сами становятся источником магнитного поля. Результирующее магнитное поле в среде является векторной суммой полей, создаваемых проводниками с током и намагниченной средой, и поэтому не равно полю в вакууме. Вещества, способные намагничиваться, называются магнетиками.

Причина намагничивания заключается в том, что во всех веществах существуют мельчайшие электрические токи – молекулярные токи. В пределах каждого атома эти токи ориентированы хаотично. Если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т.е. при одном и том же токе и при прочих равных условиях вектор в различных средах будет иметь разные значения.

Чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества.

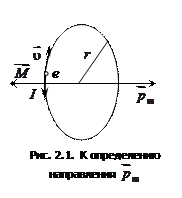
Пусть электрон движется со скоростью 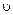в атоме по круговой орбите радиусом 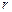. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом [см. формулу (1.2)], модуль которого:

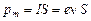, (2.1)

где 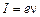– сила тока; 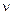– частота вращения электрона по орбите; 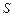– площадь орбиты.

Учитывая, что 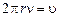, получаем:

.

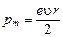Направление вектора 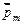образует с направлением тока правовинтовую, а с направлением движения электрона левовинтовую систему (см. рис. 2.1).

Движущийся по орбите электрон обладает моментом импульса

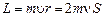, (2.2)

где 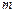– масса электрона.

Вектор 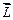называют орбитальным механическим моментом электрона. Он образует с направлением движения электрона правовинтовую систему. Следовательно, направления векторов 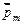и 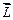противоположны. Учитывая формулы (2.1) и (2.2), получаем:

,

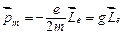где 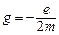– гиромагнитное отношение орбитальных моментов.

Вследствие вращения вокруг ядра электрон оказывается подобным волчку. Это обстоятельство лежит в основе так называемых магнитомеханических явлений, заключающихся в том, что намагничивание магнетика приводит к его вращению, и наоборот, вращение магнетика вызывает его намагничивание.

Экспериментально было доказано, что кроме орбитальных моментов (2.1) и (2.2) электрон обладает собственным механическим моментом импульса 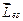, называемым спином. Считается, что спин является неотъемлемым свойством электрона, подобно его заряду и массе.

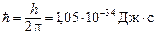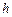Спином обладают не только электроны, но и другие элементарные частицы. Спин элементарных частиц оказывается целым или полуцелым кратным величины , где – постоянная Планка.

Спину электрона 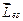соответствует собственный (спиновый) магнитный момент 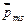, пропорциональный 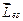и направленный в противоположную сторону:

,

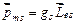где 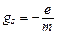– гиромагнитное отношение спиновых моментов.

Проекция собственного магнитного момента на направление вектора 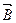может принимать только одно из двух значений:

,

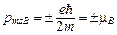где 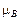– магнетон Бора, являющийся единицей магнитного момента электрона.

Общий момент атома 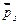равен векторной сумме магнитных моментов (орбитальных и спиновых), входящих в атом электронов:

.

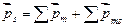Намагниченность магнетика

В дальнейшем будем различать макроскопические токи, т.е. электрические токи, протекающие по проводникам в электрических цепях, и микроскопические токи, обусловленные движением электронов в атомах и молекулах.

Намагничивание постоянных магнитов является следствием существования в них микротоков.

Для количественного описания магнитных свойств вещества ввели векторную величину – намагниченность, равную векторной сумме магнитных моментов 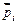атомов, которые находятся в единице объема вещества:

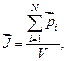
где 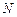– число атомов, находящихся в объеме .

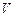Вектор индукции магнитного поля характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Следовательно, магнитное поле в веществе складывается из двух полей:

,

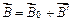где 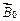– индукция магнитного поля, создаваемого макроскопическими токами, без учета свойств вещества (например, в вакууме); 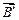– индукция магнитного поля, создаваемого микроскопическими токами.

Магнитное поле макроскопических токов описывается вектором напряженности магнитного поля 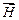. Вектор 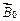связан с вектором 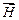следующим соотношением:

.

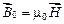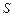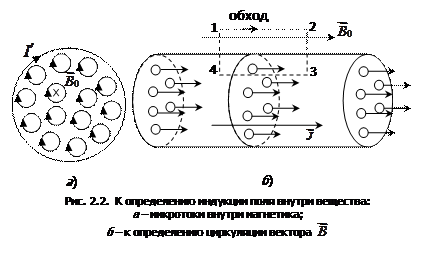
Для описания магнитного поля микротоков рассмотрим вещество (магнетик) в виде цилиндра площадью сечения и длиною находящегося в однородном магнитном поле, вектор индукции которого 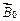(рис. 2.2, а). Вектор индукции направлен вдоль оси цилиндра от нас.

Если рассматривать любое сечение цилиндра, перпендикулярное его оси (рис. 2.2, б), то во внутренних участках сечения магнетика микротоки атомов направлены навстречу друг другу и взаимно компенсируются. Нескомпенсированными остаются лишь микротоки, выходящие на боковую поверхность цилиндра.

Ток, текущий по боковой поверхности цилиндра, создает магнитное поле, индукцию которого 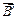можно определить по формуле для соленоида, полагая, что он состоит из одного витка:

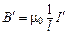, (2.3)

где 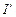– микротоки, протекающие по боковой поверхности цилиндра; 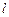– длина соленоида.

Магнитный момент, создаваемый всеми микротоками соленоида

,

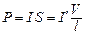где 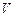– объем соленоида.

Выражая магнитный момент 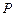через намагниченность, получаем 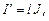или после подстановки значения 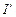в формулу (2.3) получим:

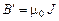или в векторной форме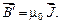

Учитывая значения 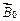и 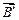, индукцию поля, создаваемого макро- и микротоками, можно записать в таком виде:

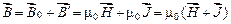. (2.4)

Экспериментально установлено, что намагниченность 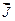пропорциональна напряженности поля, которое ее вызывает, т.е.

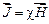, (2.5)

где 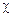– коэффициент пропорциональности, называемый магнитной восприимчивостью.

Используя выражение (2.5), результирующую индукцию поля в веществе (2.4) можно записать в виде:

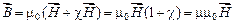. (2.6)

Безразмерная величина 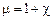называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества.

Формула (2.6) устанавливает связь между индукцией магнитного поля внутри вещества и напряженностью внешнего поля .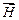

2.3. Теоремы о циркуляции векторов 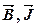и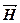

В случае определения индукции магнитного поля в вакууме было получено выражение циркуляции вектора в таком виде:

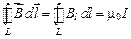. (2.7)

Микротоки в вакууме равны нулю. В случае определения индукции поля в веществе может быть использовано выражение (2.6). С учетом того, что кроме макро- присутствуют и микроскопические токи, выражение (2.7) принимает вид:

.

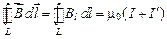Вектор характеризует поле макро- и микроскопических токов.

Определим циркуляцию вектора 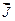. Для этого проведем замкнутый контур прямоугольной формы, одна из сторон которого находится внутри вещества (рис. 2.2., б):

.

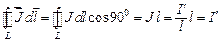Мы учли выражение .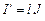

Таким образом, 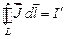. Источником вектора 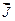являются микротоки.

Для определения циркуляции вектора 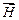воспользуемся взаимосвязью между векторам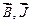и и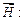

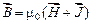, откуда .

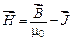В таком случае

,

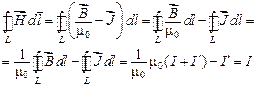
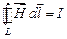т.е. источником вектора 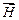являются макроскопические токи.

Виды магнетиков

Формула (2.5) определяет магнитную восприимчивость 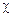единицы объема вещества. В зависимости от знака и величины 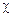все магнетики подразделяются на следующие виды.

1) Диамагнетики, у которых магнитная восприимчивость 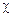отрицательна и мала по абсолютной величине, а магнитная проницаемость 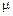меньше единицы.

2) Парамагнетики, у которых магнитная восприимчивость 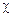положительна, а магнитная проницаемость 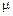несколько больше единицы.

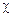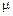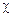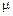3) Ферромагнетики, у которых магнитная восприимчивость положительна, магнитная проницаемость может принимать аномально большие значения. Кроме того, в отличие от диамагнетиков и парамагнетиков, для которых и не зависят от 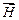, для ферромагнетиков они являются сложной функцией напряженности магнитного поля.

Диамагнетики

К диамагнетикам относятся инертные газы, металлы (Bi, Zn, Cu, Au и др.), стекло, различные смолы и другие вещества.

Рассмотрим, что происходит с атомами диамагнетика во внешнем магнитном поле на примере атома гелия. Атом гелия состоит из ядра и двух электронов (рис. 2.3). Будем считать, что электроны движутся по круговым орбитам с одинаковой по 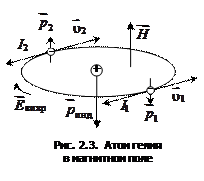величине скоростью, но в противоположных направлениях, поэтому суммарный орбитальный магнитный момент электронов равен нулю. Спиновые магнитные моменты электронов направлены в противоположные стороны и их сумма также равна нулю. Следовательно, равен нулю магнитный момент всего атома. (Магнитный момент ядра значительно меньше электронного.)

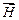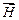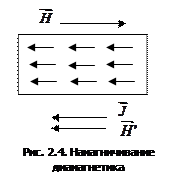
При включении внешнего магнитного поля во время его изменения от нуля до возникающее при этом вихревое электрическое поле совершает работу по увеличению скорости первого электрона и уменьшению скорости второго электрона, и суммарный магнитный момент не будет равен нулю. В таком случае . Индуцированный магнитный момент атома и направлен в сторону противоположную . Векторы намагниченности 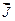и напряженности поля , сформированные вследствие диамагнитного эффекта, направлены также в сторону, противоположную 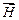(рис. 2.4).

Диамагнитный эффект обнаруживается только у тех веществ, атомы которых не обладают магнитным моментом (векторная сумма орбитальных и спиновых магнитных моментов электронов атомов равна нулю).

Теоретический расчет показывает, что индуцированный магнитный момент атома, обладающего диамагнетизмом

, (2.8)

где и 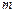– соответственно заряд и масса электрона; – средний квадрат расстояния от электрона до ядра.

Если значение магнитного момента атома (2.8) умножить на число атомов в одном моле (число Авогадро ), получим намагниченность одного моля вещества:

.

Сравнивая последнее выражение с формулой (2.5), находим магнитную восприимчивость одного моля вещества:

.

Подставляя численные значения , , , 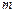и , получаем, что молярная диамагнитная восприимчивость имеет порядок м³/моль, что согласуется с экспериментом.

Парамагнетики

Если магнитный момент атома не равен нулю, то вещество относится к парамагнетикам (рис. 2.5, а). Если поместить парамагнетик во внешнее магнитное поле, магнитные моменты атомов стремятся установиться вдоль вектора напряженности 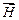, а тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля (рис. 2.5, б), тем большая, чем больше 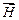и тем меньшая, чем выше температура.

Кюри экспериментально установил закон, согласно которому восприимчивость парамагнитного вещества равна:

, (2.9)

где – постоянная Кюри, зависящая от рода вещества; – термодинамическая температура.

Теория, объясняющая поведение парамагнетика во внешнем поле была предложена Ланжевеном. В этой теории парамагнетик представлен в виде совокупности магнитных стрелок (газа магнитных стрелок), принимающих участие в тепловом движении и взаимодействующих с внешним магнитным полем.

В результате для магнитной восприимчивости Ланжевеном было получено следующее выражение:

, (2.10)

где 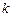– постоянная Больцмана.

Сравнивая формулы (2.9) и (2.10), получаем, что постоянная Кюри

.

Значение , определенное по формуле (2.10), в основном согласуется с опытом, однако в сильных полях и при низких температурах наблюдается отступление от пропорциональности между намагниченностью 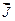и напряженностью 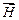поля; в частности, может наступить состояние магнитного насыщения, при котором все выстраиваются по полю и дальнейшее увеличение 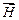не приводит к увеличению .

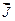Ферромагнетики

К ферромагнитным веществам относятся железо, никель, кобальт, гадолиний, их сплавы и соединения. Кроме того, к ним относятся некоторые сплавы и соединения марганца и хрома с неферромагнитными соединениями. В последнее время широкое распространение получили вещества на основе редкоземельных соединений, в частности самария. Магнитные свойства таких веществ даже превышают свойства обычных ферромагнетиков.

Из таких веществ обычно приготавливают магнитные порошки, из которых прессуют необходимые магнитные детали.

Существуют также ферромагнитные полупро­водники, которые называются ферритами.

Свойства ферромагнетиков сильно отличаются от магнитных свойств уже рассмотренных диа- и парамагнетиков, что наглядно демонстрирует экспериментальный график зависимости намагниченности от напряженности магнитного поля (рис. 2.6).

Для ферромагнетиков на начальном этапе намагничивания еще наблюдается прямая пропорциональная зависимость от , затем эта зависимость нарушается, происходит насыщение, и в дальнейшем намагниченность ферромагнетиков остается постоянной и не зависящей от напряженности поля .

Соответственно экспериментальный график зависимости индукции 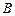магнитного поля в ферромагнетике от напряженности поля имеет вид, изображенный на рис. 2.7. Характер этой кривой объясняется следующим образом. Можно записать:

.

Отсюда следует, что на начальном этапе индукция поля в ферромагнетике растет и за счет роста и за счет роста . Затем вектор намагниченности, дойдя до насыщения, остается постоянным и рост индукции объясняется только ростом .

Кроме того, оказалось, что если довести намагниченность до насыщения (точка 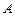на рис. 2.8) и затем уменьшать напряженность магнитного поля, то индукция 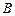следует не по первоначальной кривой , а изменяется в соответствии с кривой . В результате, когда напряженность внешнего поля станет равной нулю, намагниченность не исчезает и характеризуется величиной , которая называется остаточной индукцией.

Чтобы достигнуть состояния, при котором индукция поля в ферромагнетике снова станет равной нулю, необходимо приложить поле напряженностью , противоположное полю, вызвавшему намагничивание. Напряженность называется коэрцитивной силой.

Таким образом, при действии на ферромагнетик переменного магнитного поля индукция меняется в соответствии с кривой (рис. 2.8), которая называется петлей гистерезиса.

Можно показать, что площадь петли гистерезиса прямо пропорциональна энергии, затрачиваемой на перемагничивание единицы объема ферромагнетика за каждый цикл. Действительно, размерность произведения 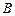на равна:

.

По значению коэрцитивной силы различают типы ферромагнетиков. Ферромагнетики с большим значением называются жесткими ферромагнетиками. Они используются для изготовления постоянных магнитов. У таких ферромагнетиков площадь петли гистерезиса достаточно велика, следовательно, велика и энергия перемагничивания.

Ферромагнетики с малым значением называются мягкими ферромагнетиками. Такие ферромагнетики используются для изготовления сердечников трансформаторов. Петля гистерезиса у них имеет малую площадь, а соответственно, мала энергия перемагничивания и, как следствие, малы потери.

График зависимости магнитной проницаемости ферромагнетика от напряженности магнитного поля представлен на рис. 2.9. Как видно, магнитная проницаемость вначале растет, достигает максимума, а затем спадает до единицы. Такой ход зависимости можно объяснить исходя из связи между магнитной проницаемостью и магнитной восприимчивостью .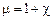

Тогда запишем:

.

Отсюда вытекает: ,

т.е. 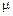сначала растет за счет роста , а затем, когда достигается насыщение и прекращается рост 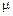начинает падать, так как отношение стремится к нулю.

Исключительные магнитные свойства ферромагнетиков объясняются их так называемой доменной структурой.

Внешние электроны атомов ферромагнетиков находятся на относительно близких расстояниях при формировании кристаллической решетки. Как мы уже знаем, электрон обладает собственным спиновым магнитным моментом. На таких малых расстояниях происходит интенсивное взаимодействие спиновых магнитных моментов внешних электронов, которое называется обменным или спин-спиновым взаимодействием. В результате этого взаимодействия магнитные моменты электронов оказываются одинаково направленными в значительных по размеру макроскопических областях, которые называются доменами. Домены имеют размеры порядка .

В результате весь объем ферромагнетика разбивается на домены или области спонтанной намагниченности. Но ориентация магнитных моментов этих доменов произвольная, так что суммарный магнитный момент образца ферромагнетика равен нулю.

При наложении внешнего поля напряженностью ферромагнетики намагничиваются (см. рис. 2.7). Это намагничивание состоит в том, что увеличиваются размеры благоприятных доменов и, соответственно, уменьшаются размеры неблагоприятных доменов. При этом под благоприятными доменами понимаются такие, у которых направление магнитного момента близко к направлению внешнего поля и наоборот. Следовательно, когда намагничивание ферромагнетиков достигает некоторых предельных напряжений, происходит скачкообразное изменение физических размеров доменов, перемещение их границ. В результате в образце ферромагнетика возникают акустические волны, которые можно услышать, используя соответствующий усилитель. Эти характерные трески, которые наблюдаются при намагничивании ферромагнетика, называются скачками Баркгаузена. При дальнейшем росте напряженности поля происходит ориентация доменов по внешнему полю.

Когда процесс роста и ориентации благоприятных доменов закончится, происходит так называемое насыщение. При дальнейшем росте поля рост намагниченности ферромагнетиков не происходит.

При повышении температуры и достижении некоторой критической температуры , называемой точкой Кюри, доменная структура ферромагнетиков исчезает, они теряют свои ферромагнитные свойства и становятся обычными парамагнетиками. При охлаждении и понижении температуры ниже точки Кюри, доменная структура ферромагнетиков восстанавливается, восстанавливаются и их исключительные магнитные свойства. Для железа температура Кюри составляет , для никеля .