Основные законы магнитного поля

Теорема Гаусса для поля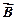

Поток вектора 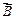сквозь любую замкнутую поверхность равен нулю:

.

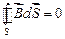Эта теорема выражает собой в постулативной форме тот экспериментальный факт, что линии вектора 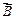не имеют ни начала, ни конца. Поэтому число линий вектора 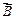, выходящих из любого объема, ограниченного замкнутой поверхностью 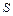, всегда равно числу линий, входящих в этот объем.

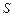Отсюда вытекает важное следствие: поток вектора сквозь поверхность , ограниченную некоторым замкнутым контуром, не зависит от формы поверхности .

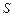Циркуляция вектора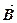

Циркуляцией вектора по заданному замкнутому контуру называется интеграл

,

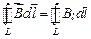где 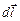– вектор элементарной длины контура, направленный вдоль обхода контура; 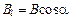– составляющая вектора 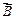в направлении касательной к контуру (с учетом выбранного направления обхода); 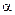– угол между векторами и .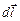

Теорема о циркуляции вектора 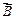: циркуляция вектора 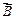по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:

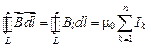(1.12)

где 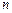– число проводников с токами, охватываемых контуром 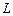произвольной формы.

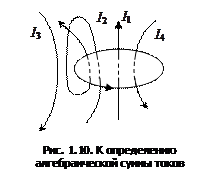
Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 1.10.

.

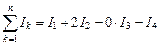Теорема о циркуляции вектора имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био–Савара–Лапласа.

1.13. Применение теоремы о циркуляции вектора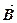

Магнитное поле прямого тока

Пусть постоянный ток 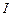течет вдоль бесконечно длинного прямого провода, имеющего круглое сечение радиусом 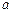. Найти индукцию поля снаружи и внутри провода.

Линии вектора имеют вид окружностей с центром на оси провода. Причем модуль вектора должен быть одинаков во всех точках на расстоянии 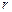от оси провода. Поэтому по теореме о циркуляции вектора для круглого контура 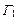(рис. 1.11, а) 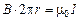, следовательно, вне провода

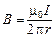, ( ). (1.13)

Решение этой задачи с помощью закона Био–Савара–Лапласа оказывается гораздо более сложным.

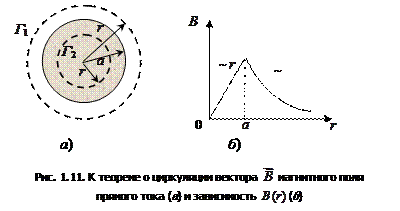
Из соображений симметрии следует, что линии вектора внутри провода являются тоже окружностями. По теореме о циркуляции вектора для круглого контура (рис. 1.11, а) 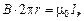, где 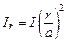– ток, охватываемый данным контуром. Отсюда находим, что внутри провода

, .

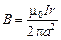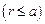Зависимость 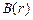показана на рис. 1.11, б.

Если провод имеет вид трубки, то снаружи индукция определяется формулой (1.13), а внутри – магнитное поле отсутствует. Это также легко показать с помощью теоремы о циркуляции вектора .

Магнитное поле соленоида

l

Пусть ток 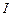течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Пусть на единицу длины соленоида приходится 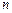витков проводника. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно приближенно заменить замкнутым витком. Будем также полагать, что сечение проводника настолько мало, что ток в соленоиде можно считать текущим по его поверхности.

Экспериментальное изучение магнитного поля соленоида показывает, что внутри соленоида поле является однородным, вне соленоида – неоднородным и очень слабым.

Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции выберем замкнутый прямоугольный контур (рис. 1.12). Циркуляция вектора по данному контуру равна 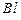, и контур охватывает ток 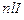, где 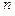– число витков на единицу длины соленоида. Согласно теореме о циркуляции (1.12) 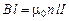, откуда следует, что внутри длинного соленоида

,

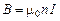т.е. поле внутри длинного соленоида однородно.

Магнитное поле тороида

Тороид представляет собой провод, навитый на каркас, имеющий форму тора (рис. 1.13).

Как показывает опыт, магнитное поле сосредоточено внутри тороида, вне его поле отсутствует.

Линии магнитной индукции в данном случае представляют собой окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиусом 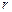. Если контур расположен внутри тороида, он охватывает ток 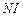, где 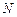– число витков тороида, 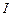– ток в проводе. По теореме о циркуляции (1.12) 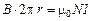, следовательно, магнитная индукция внутри тороида .

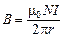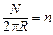Учитывая, что , где 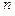– число витков на единицу длины тороида, 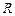– внешний радиус тора, получаем:

.
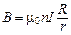