Создание нерелятивистской квантовой механики
Такие новые представления и принципы были созданы плеядой выдающихся физиков XX в. в 1925—1927 гг.: В. Гейзенберг установил основы так называемой матричной механики; Л. де Бройль, а за ним Э. Шредингер разработали волновую механику. Вскоре выяснилось, что и матричная механика, и волновая механика — различные формы единой теории, получившей название квантовой механики.
К созданию матричной механики В. Гейзенберг пришел в результате исследований спектральных закономерностей, а также теории дисперсии, где атом представлялся некоторой символической математической моделью — как совокупность виртуальных гармонических осцилляторов. Представления об атоме как о системе, состоящей из ядра и вращающихся вокруг него электронов, которые обладают определенной массой, движутся с определенной скоростью по определенной орбите, нужно понимать лишь как аналогию для установления математической модели. Указанный метод исследования и развил Гейзенберг, распространив его вообще на теорию атомных явлений.
В 1926 г. Гейзенберг впервые высказал основные положения квантовой механики в матричной форме. Теория атомных явлений, по Гейзенбергу, должна ограничиваться установлением соотношений между величинами, которые непосредственно измеряются в экспериментальных исследованиях («наблюдаемыми» величинами, в терминологии Гейзенберга) — частотой излучения спектральных линий, их интенсивностью, поляризацией и т.п. «Ненаблюдаемые» величины, такие, как координаты электрона, его скорость, траектория, по которой он движется, и т.д., не следует использовать в теории атома.
Однако в согласии с принципом соответствия новая теория должнa определенным образом соответствовать классическим теориям, т.е. соотношения величин новой теории должны быть аналогичными соотношениям классических величин. При этом каждой классической величине нужно найти соответствующую ей квантовую величину и, пользуясь классическими соотношениями, составить соответствующие им соотношения между найденными квантовыми величинами. Такие соответствия могут быть получены только из операций измерения.
Анализируя закономерности измерения величин в квантовой механике, Гейзенберг приходит к важному принципиальному результату о невозможности одновременного точного измерения двух канонически сопряженных величин и устанавливает так называемое соотношение неопределенностей
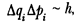
где Δqi— точность измерения какой-либо из координат частицы; Δpi — точность одновременного измерения соответствующего импульса; h— постоянная Планка.
Этот принцип является основой физической интерпретации квантовой механики.
Второе направление в создании квантовой механики сначала развивалось в работах Л. де Бройля. Он высказал идею о волновой природе материальных частиц. На основании уже установленного факта одновременно и корпускулярной, и волновой природы света, а также оптико-механической аналогии де Бройль пришел к идее о существовании волновых свойств любых частиц материи.
На первые работы де Бройля, в которых высказывалась идея волн, связанных с материальными частицами, не обратили серьезного внимания. Де Бройль впоследствии писал, что высказанные им идеи были приняты с «удивлением, к которому несомненно примешивалась какая-то доля скептицизма». Но не все скептически отнеслись к идеям де Бройля. Особенно сильное влияние идеи де Бройля оказали на Э. Шрёдингера, который увидел в них основу для создания новой теории квантовых процессов. В 1926 г. Шрёдингер, развивая идеи де Бройля, построил так называемую волновую механику.
Шрёдингер приходит к мысли, что квантовые процессы следует понимать как некие волновые процессы, характеризуемые волновой функцией Ψ. Тогда образ материальной точки, занимающей определенное место в пространстве, строго говоря, является приближенным и может быть сохранен только при рассмотрении макропроцессов, подобно тому как мы пользуемся представлением о световом луче, которое теряет смысл, если рассматривать явления дифракции и интерференции. Функция Ψ должна удовлетворять волновому уравнению («уравнение Шрёдингера»). Шрёдингер поставил вопрос о связи его теории с теорией Гейзенберга и показал, что при всем различии исходных физических положений они математически эквивалентны.
Иначе говоря, в квантовой механике разница между полем и системой частиц исчезает. Так, например, электрон, вращающийся вокруг ядра, можно представить как волну, длина которой зависит от ее скорости. Там, где укладывается целое число длин волн электрона, волны складываются и образуют боровские разрешенные орбиты. А там, где целое число длин волн не укладывается, гребни волн компенсируют впадины, там орбиты не будут разрешены.
Волновая механика получила прямое экспериментальное подтверждение в 1927г., когда К-Дж. Дэвиссон и П. Джермер обнаружили явление дифракции электронов. Кроме того, выяснилось, что правильно и количественное соотношение для длин «волн де Бройля».
Квантовая механика — теоретическая основа современной химии. Ядро атома с порядковым номером N и массовым числом М содержит N протонов и (М- N) нейтронов (всего М нуклонов). Число электронов оболочек равно числу протонов в ядре, поэтому в нормальном состоянии атом нейтрален. Электроны распределяются на оболочках в строгом порядке: на первой к ядру не более 2 электронов; на второй — не более 8; на третей — не более 18 и т.д. Когда два атома сталкиваются, они или объединяются вместе, обобществляя свои оболочки, или вновь расходятся после перераспределения электронов. Число электронов на внешней оболочке и определяет химическую активность элемента.
С помощью квантовой теории удалось построить также более совершенные теории твердого тела, электрической проводимости, термоэлектрических явлений и т.д. Она дала основания для построения теории радиоактивного распада, а в дальнейшем стала базой для ядерной физики.
Вслед за основополагающими работами Шрёдингера по волновой механике были предприняты первые попытки релятивистского обобщения квантово-механических закономерностей, и уже в 1928 г. П. Дирак заложил основы релятивистской квантовой механики.
