Работа в электрическом поле. Потенциальность электростатического поля

Поскольку на заряженную частицу в электрическом поле действует электрическая сила, при ее движении совершается механическая работа. Механическая работа, как известно, определяется скалярным произведением силы на перемещение, а поскольку в разных точках траектории действующая сила различна (например, поле другой заряженной частицы изменяется обратно пропорционально квадрату расстояния от нее), составляя это произведение, нужно брать бесконечно малое перемещение:

;

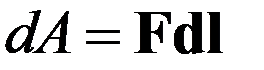в механике для обозначения перемещения обычно применяется ds; мы используем обозначение dl, поскольку dS и dS мы будем применять для обозначения элемента некоторой поверхности.

Работа при перемещении на конечное расстояние складывается из бесконечного числа таких элементарных работ, т. е. интегралом вида

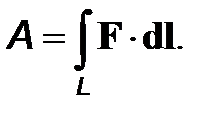(1)

Поскольку электрическая сила представляется в виде F=qE, выражение для работы в электрическом поле можно переписать в виде

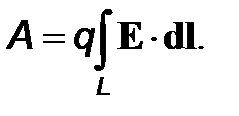(2)

E

R

dl

L

q0

R1

R2

q

В математическом анализе известны способы вычисления таких интегралов, называемых контурными (или криволинейными интегралами II рода), для конкретных функциональных зависимостей подынтегрального выражения от координат для заданных кривых, вдоль которых осуществляется интегрирование. Важно иметь в виду, что это не обыкновенный интеграл, а контурный, поэтому вместо привычных пределов

интегрирования указывается область интегрирования путем использования для обозначения этой области символа внизу от знака интеграла (в данном случае L). Но всегда можно трактовать интеграл как предел суммы бесконечно большого числа бесконечно малых слагаемых. В ряде задач на основе этого представления можно контурный интеграл свести к обыкновенному и вычислить его знакомыми методами.

Рассмотрим, чем определяется работа при перемещении точечного заряда q в электростатическом поле неподвижного точечного заряда q₀ из точки 1 с радиус-вектором R₁ в точку 2 с радиус-вектором R₂ вдоль кривой L. Подставим выражение для напряженности поля точечного заряда (1.5) в интеграл (2), определяющий работу:

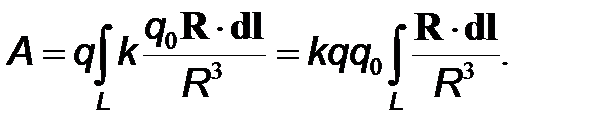(3)

Преобразуем скалярное произведение, входящее в подынтегральное выражение.

q0

R

R+dl

E

dl

a

q

dR

Из рис. (справа) видно, что

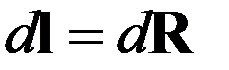
Откуда

Чтобы убедиться в справедливости последнего соотношения, достаточно взять дифференциал

от обеих частей тождества

.

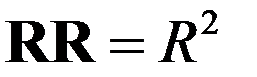Из последних соотношений видно, что работа при перемещении наdl определяется изменением dR расстояния R от заряда q₀ и напряженностью поля E в этом месте.

После подстановки этого соотношения в интеграл (3) последний становится обыкновенным с пределами интегрирования R₁ и R₂ , представляющими собой расстояния от заряда q₀ до точек 1 (начальной) и 2 (конечной), и легко вычисляется:

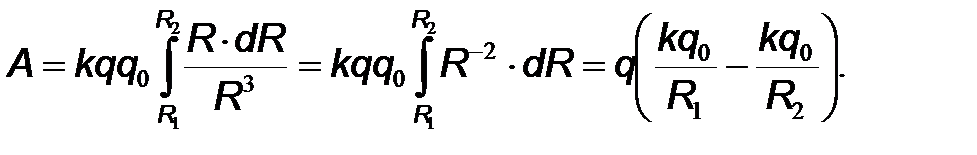(4)

Выражение в скобках не содержит величин, относящихся к перемещаемому заряду q, и характеризует электрическое поле заряда q₀. Величина

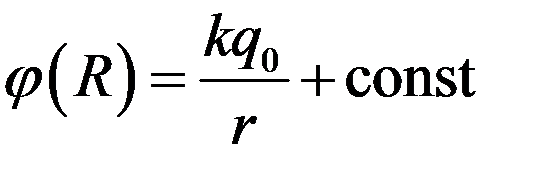
носит название потенциала электростатического поля точечного заряда q₀ Потенциал, являясь функцией координат, являет собой пример скалярного поля. Входящая в определение потенциала константа аддитивна, т. е. одинакова для всех точек пространства. Обычно принимают эту константу равной нулю. Это означает, что потенциал поля на бесконечности принимается равным нулю. Зная потенциал поля заряда q₀, можно вычислить потенциальную энергию заряда q, находящегося в этом поле. Для этого достаточно умножить заряд q на потенциал поля заряда q₀ в точке, в которой находится заряд q. Разность потенциальных энергий равна работе:

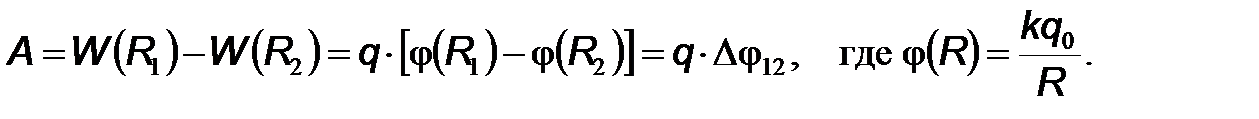(5)

Этот результат мы получили для случая, когда электростатическое поле создавалось одним зарядом q₀. Мы знаем, что любое распределение заряда можно представить как систему точечных зарядов. Если, например, электростатическое поле создается N неподвижными точечными зарядами q₁,…,q_N, положение которых определяется радиус-векторами r₁,…,r_N, выражение для работы с использованием формулы для напряженности поля E(r) предстанет в виде

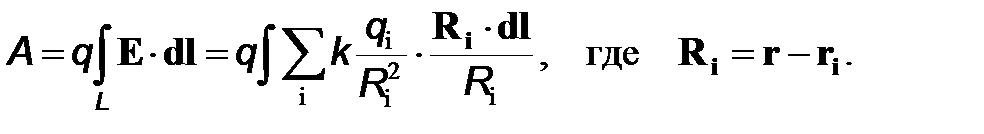(6)

Далее изменяем порядок интегрирования и суммирования и используем соотношения (4):

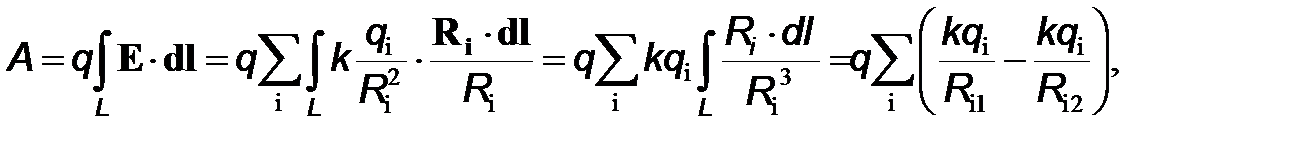
где 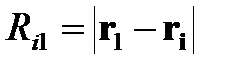и 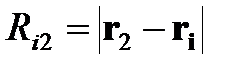представляют собой расстояния от i-го заряда соответственно до точек 1 и 2. Используя определение потенциала точечного заряда, последнее выражение можно представить в виде

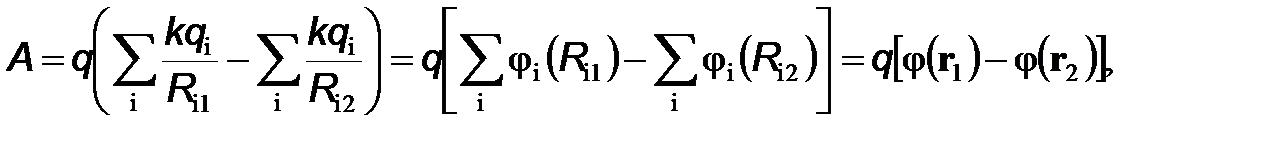(7)

где

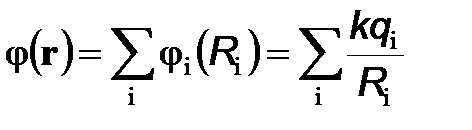(8)

по определению представляет собой потенциал системы неподвижных точечных зарядов в точке с радиус-вектором r (при условии, что на бесконечности потенциал поля этой системы зарядов равен нулю). Соотношение (8) легко обобщается на случай наличия непрерывно распределенного заряда:

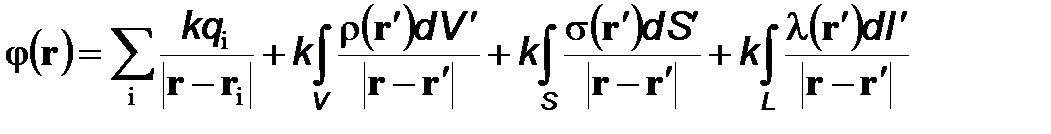, (9)

где в первый интеграл входят заряды, непрерывно распределенные по объемам, которые здесь обозначены как V, во второй–заряды, непрерывно распределенные по поверхностям заряженных тел, и эти поверхности здесь обозначены буквой S; в третий интеграл входят заряды, непрерывно распределенные на телах, толщинами которых можно пренебречь. Штрих у dV, dS, dl подчеркивает, что положение этих элементов объема, поверхности и длины определяется радиус-вектором r¢, а не r.

Как видно из формулы (7),

Работа при перемещении заряда в электростатическом поле не зависит от пути, по которому перемещается заряд, и определяется только величиной перемещаемого заряда и разностью потенциалов поля в исходной и конечной точках.