Поток вектора напряженности электрического поля. Теорема Гаусса
Электрическое поле можно изобразить графически с помощью линий напряженности электрического поля (силовые линии) (рис. 2.4).
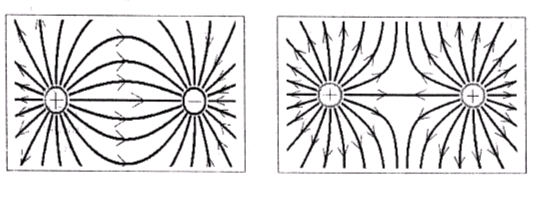
Рис.2.4
Линиями напряженности электрического поля называются линии, касательная в каждой точке которых совпадает с направлением вектора напряженности. Они начинаются на положительных зарядах и заканчиваются на отрицательных зарядах или уходят в бесконечность. Число линий напряженности можно, в принципе, проводить сколь угодно много. Однако, условились проводить их с такой густотой, чтобы число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, было пропорционально модулю вектора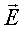 
.
Потоком вектора напряженности электрического поля через элементарную площадку dS называется произведение модуля вектора напряженности 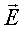на площадь элементарной поверхности и на косинус угла между нормалью к поверхности 
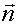и направлением вектора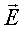
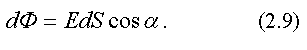
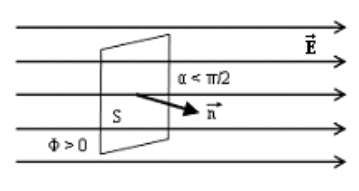
Рис.2.5
На рис. 2.5 показаны линии напряженности 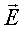, 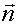- нормаль к площадке dS и угол α.
Для произвольной замкнутой поверхности S поток вектора 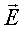через эту поверхность равен
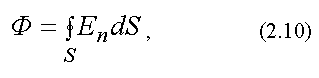
где интеграл берется по замкнутой поверхности S; En - проекция вектора 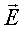на нормаль к площадке dS, 
.
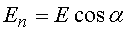Нормаль к замкнутой поверхности выбирается внешняя, а поток может быть положительным или отрицательным. Подчеркнем, что поток пропорционален числу силовых линий, пронизывающих поверхность.
Теорема Гаусса
Теорема Гаусса формулируется следующим образом.
Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, деленной на электрическую постоянную
Доказательство проведем в несколько этапов.
1. Рассмотрим замкнутую поверхность в виде сферы радиуса r, в центр которой помещен точечный заряд q (рис. 2.6).
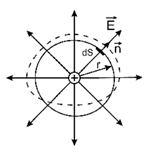
Рис.2.6
Напряженность электрического поля, созданного точечным зарядом в вакууме, вычисляется по формуле (2.4) при ε = 1
.
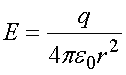Для сферы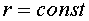 
, следовательно, 
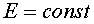, а также 
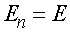, так как 
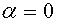. Поток вектора 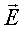в этом случае равен
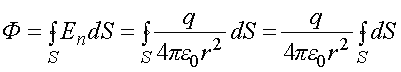
Интеграл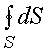 
равен площади сферы
.
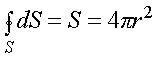Тогда поток вектора 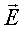равен
.
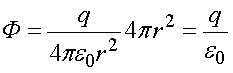Ответ сравните с формулой (2.11) и убедитесь, что теорема доказана. Напомним, что поток пропорционален числу силовых линий, пронизывающих замкнутую поверхность.
2. Если замкнутая поверхность отличается от сферы (см. рис. 2.6, пунктирная линия), то поток вектора 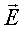не изменится, так как не изменяется число силовых линий, пронизывающих эту поверхность.
3. Если внутри замкнутой поверхности находится не один заряд, а несколько, то результирующая напряженность электрического поля находится по принципу суперпозиции (2.8). Тогда потоки и заряды складываются алгебраически, т. е. с учетом знаков, и теорема Гаусса, формула (2.11), оказывается справедливой.
Теорема Гаусса применяется для вычисления электрических полей, созданных протяженными зарядами, например, заряженной нитью, плоскостью и т. д. С помощью теоремы Гаусса получены формулы (2.5), (2.6) и (2.7).