Кинематика поступательного и вращательного движения

МЕХАНИКА

Кинематика поступательного и вращательного движения

Предмет механики

Механикой называется раздел физики, в котором изучаются закономерности механического движения и причины, вызывающие или изменяющие это движение. Механика делится на три раздела: кинематику, динамику и статику.

Кинематика изучает движение без учета причин, его вызывающих.

Динамика изучает движение с учетом причин, его вызывающих.

Статика - наука о равновесии.

Существует классическая, релятивистская и квантовая механика.

Классическая механика изучает движение макроскопических тел со скоростями, много меньшими скорости света в вакууме (v<<c, c=3·10⁸м/c).

Релятивистская механика (или теория относительности) изучает движение тел со скоростями, соизмеримыми со скоростью света в вакууме.

Квантовая механика изучает движение микрочастиц (отдельные атомы, элементарные частицы).
Изучение нашего курса начнем с классической механики.

Механическое движение. Модели в механике

Механическим движением называется процесс изменения взаимного расположения тел или их частей в пространстве и с течением времени. Для описания движения в механике используются физические модели. Простейшими моделями в механике являются материальная точка и абсолютно твердое тело.

Материальной точкой называется обладающее массой тело, размерами которого можно пренебречь в условиях данной задачи. Например, при вычислении траектории, по которой Земля движется вокруг Солнца, Землю можно рассматривать как материальную точку, так как ее радиус в 24 000 раз меньше радиуса ее орбиты. При рассмотрении движения тел по поверхности Земли она должна рассматриваться как протяженный объект.

Любое тело можно рассматривать как совокупность материальных точек.

Абсолютно твердым телом называется тело, деформациями которого можно пренебречь в условиях данной задачи.

Тело может двигаться поступательно и вращательно.

Поступательным движением называется такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе. При поступательном движении все точки тела движутся одинаковым образом. Поэтому достаточно рассмотреть движение одной точки тела, например, центра тяжести, чтобы говорить о движении тела в целом.

Вращательным движением называется движение, при котором все точки тела описывают окружности. Центры этих окружностей лежат на прямой, называемой осью вращения. В общем случае движение твердого тела можно представить как результат сложения поступательного и вращательного движений.

Скорость

Скорость характеризует направление и быстроту перемещения точки или тела в пространстве.

Средней скоростью называется отношение перемещения к промежутку времени, за которое это перемещение произошло

Средняя скорость направлена так же, как вектор перемещения 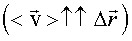(рис. 1.3).

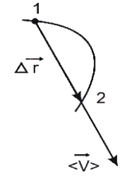
Рис.1.3

Модуль средней скорости равен .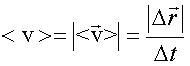

Скоростью (или мгновенной скоростью) материальной точки называется предел отношения ее перемещения к промежутку времени, за которое это перемещение произошло, при бесконечном убывании промежутка времени, т. е.

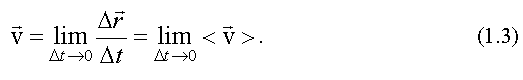
В математике такой предел называется производной. Скорость равна производной от радиус-вектора по времени

Скорость направлена по касательной к траектории, так как при 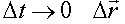сливается
с касательной (рис. 1.4).

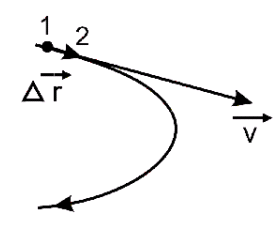
Рис.1.4

При 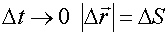, поэтому .

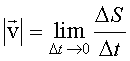Модуль скорости равен производной от пути по времени:

Силы в механике

Силой называется мера действия одного тела на другое, т. е. мера взаимодействия тел.

В физике известно четыре вида взаимодействия тел:

· ядерное (между нуклонами атомного ядра);

· слабое (при распаде некоторых элементарных частиц);

· электромагнитное (между частицами, имеющими электрический заряд);

· гравитационное (между любыми частицами).

Ядерное и слабое взаимодействие в механике не рассматриваются. Электромагнитное взаимодействие проявляется в механике в виде сил трения и упругости. Гравитационное взаимодействие является самым "слабым". Однако, при наличии больших масс (планеты, звезды и т. д.) оно является весьма существенным. Поэтому для большинства явлений механики, происходящих на Земле, нужно учитывать силу тяготения (т. е. гравитационное взаимодействие).

Гравитационная сила (или сила всемирного тяготения) является фундаментальной силой. Гравитация является всеобщим законом для всей Вселенной. Закон всемирного тяготения, открытый Ньютоном, формулируется следующим образом.

Два тела (рассматриваемые как материальные точки) притягиваются друг к другу по прямой, их соединяющей, с силами, прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними

где 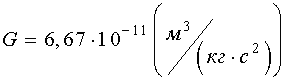- гравитационная постоянная.

Перечислим некоторые нефундаментальные силы, которые используются при решении задач в механике.

Сила тяжести

где 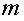- масса тела, 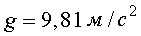- ускорение свободного падения.

Сила трения

где 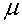- коэффициент трения, N- сила нормального давления. Сила трения направлена против движения.

Сила упругости

,

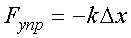где k- коэффициент упругости, 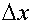- деформация (изменение длины тела): .
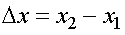Формулу для силы упругости можно записать проще, если считать, что .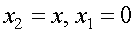

Тогда:

Сила упругости вычисляется по закону Гука, согласно которому упругая деформация пропорциональна действующей на тело силе.

Масса и импульс тела

Опыт показывает, что всякое тело сопротивляется попыткам изменить его состояние. Это свойство называется инертностью.

Масса - это мера инертности тела.

Масса также определяет гравитационные свойства и определяется количеством вещества, заключенного в теле.

Импульс тела равен произведению массы тела на его скорость. Это векторная величина

Законы Ньютона

В основе классической динамики лежат три закона Ньютона, полученные как результаты обобщения опытных фактов.

I закон Ньютона называют законом инерции.

Закон сохранения импульса

Закон сохранения импульса является одним из основных законов природы. В механике его можно получить из II и III законов Ньютона. Он справедлив для системы материальных точек, на которые либо не действуют внешние силы, либо векторная сумма всех внешних сил равна нулю. Система, на которую не действуют внешние силы, называется замкнутой системой.

Для вывода закона сохранения импульса рассмотрим замкнутую систему, состоящую из трех тел. (рис. 1.8). Тогда между телами системы действуют только внутренние силы.

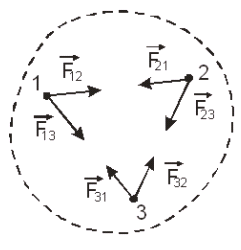
Рис.1.8

По III закону Ньютона (1.24)

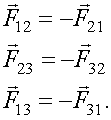
По II закону Ньютона (1.23)

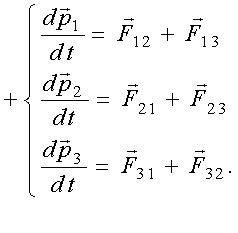
Сложим левые и правые части уравнений

.

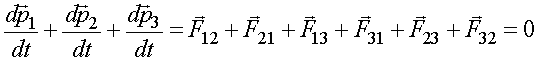Преобразуем это уравнение

.

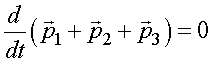Назовем 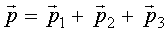импульсом системы.

Импульсом системы называется векторная сумма импульсов тел, входящих в систему.

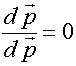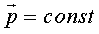Тогда: и , если внешние силы отсутствуют.

Закон сохранения импульса читается так: импульс замкнутой системы сохраняется.

Отметим, что импульс сохраняется и для незамкнутых систем при условии, что векторная сумма внешних сил равна нулю.

На основе закона сохранения импульса можно объяснить отдачу оружия при стрельбе, реактивное движение и т. д. Закон сохранения импульса является одним из важнейших законов природы. Он выполняется всегда и везде - в космосе и микромире, для макротел и микрочастиц.

Работа в механике. Мощность

Понятие работа является обобщением повседневного опыта человека. Но в механике это понятие является более узким и более точным, чем в быту.

Работой постоянной силы в механике называется произведение модуля вектора силы на модуль вектора перемещения и на косинус угла между направлением силы и направлением перемещения (рис. 1.9)

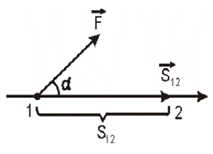
Рис.1.9

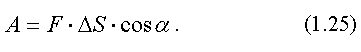
Эта формула справедлива, если тело движется прямолинейно и на него действует постоянная сила. Длина пути тогда равна модулю вектора перемещения .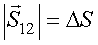

Из формулы (1.25) следует, что работа может быть положительной (если 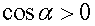), отрицательной ( 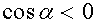) или равной нулю ( 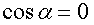). Если работа положительная ( A > 0 ), то это значит, что внешние силы совершают над телом работу. Если работа отрицательная ( A < 0 ), то тело совершает работу над внешними телами.

Единицей работы в системе СИ является джоуль (Дж)

.

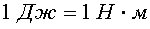В общем случае, движение может происходить по криволинейной траектории под действием переменной силы (рис. 1.10).

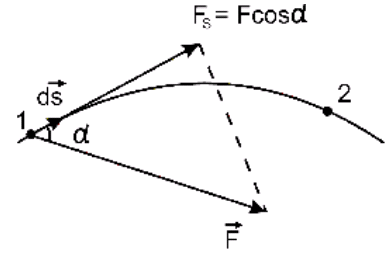
Рис.1.10

Тогда сначала нужно вычислить элементарную работу на малом участке пути, на котором движение можно считать прямолинейным, а силу постоянной

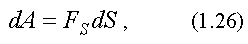
где 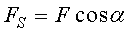; F_s - проекция силы на направление перемещения.

Суммарную работу находят интегрированием

По этой формуле вычисляется работа переменной силы.

Работа, совершаемая в единицу времени, называется мощностью

Единица мощности - ватт (Вт)

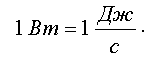
Механическая энергия

Проблема энергии касается каждого человека. От потребления энергии непосредственно зависит благосостояние людей, поэтому надо четко представлять себе, что такое энергия, и как она распределяется.

В соответствии с различными формами движения материи существуют разные виды энергии: механическая, химическая, тепловая, электрическая, ядерная и т. д. Для сравнения различных форм движения материи требуется общий эквивалент, подобно тому, как деньги являются общим эквивалентом, позволяющим сравнивать различные товары. В физике мерой перехода одних форм движения в другие является энергия. Изменение энергии связано с совершением работы. Итак, энергией называется способность тела совершать работу.

В механике тело способно совершить работу в двух случаях:

1) если оно движется, т. е. обладает кинетической энергией;

2) если оно находится в потенциальном поле сил, т. е. обладет потенциальной энергией.

Кинетическая энергия

Кинетической энергией называется энергия движущегося тела. Найдем формулу для кинетической энергии и покажем, что изменение кинетической энергии равно работе равнодействующей силы.

Элементарная работа равна

.

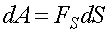Используя формулы (1.22), (1.8), (1.5), получим

.

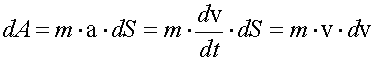Суммарная работа по формуле (1.27) равна

.

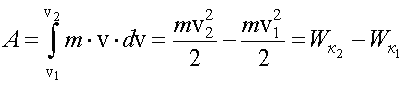Отсюда кинетическая энергия вычисляется по формуле

Кинетическая энергия всегда положительная, она измеряется в тех же единицах, что и работа. Если A > 0, то 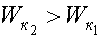, т. е. кинетическая энергия тела возрастает, следовательно, внешние силы над телом совершают работу.

Если A<0, то 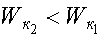, т. е. кинетическая энергия тела убывает, значит тело совершает работу.

Консервативные силы

Примерами консервативных сил являются сила тяжести и сила упругости.

Основным свойством консервативных сил является то, что работа консервативных сил не зависит от формы траектории. Покажем это на примере работы силы тяжести ( 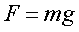, см. формулу (1.18)).

Покажем, что работа силы тяжести (формула (1.25)) одинакова для двух разных путей (для пути 1 - 3 и пути 1 - 2 - 3), обозначения длин путей приведены на рис. 1.11

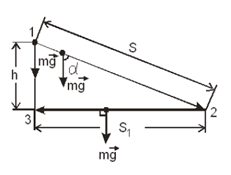
Рис.1.11

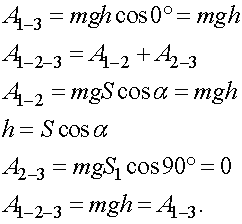
Из последней формулы следует, что работа силы тяжести не зависит от формы траектории.

Консервативными силами называются силы, работа которых не зависит от формы траектории, а определяется только начальной и конечной координатами тел. Силы, которые не удовлетворяют этому правилу, называются неконсервативными. Примером неконсервативных сил является сила трения.

Потенциальная энергия

Потенциальной энергией называется энергия, обусловленная взаимным расположением тел или их частей друг относительно друга.

Универсальной формулы для расчета потенциальной энергии нет.

Потенциальная энергия гравитационного взаимодействия двух тел равна:

где m₁ и m₂ - массы взаимодействующих тел, r - расстояние между центрами масс, 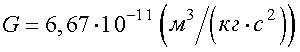- гравитационная постоянная.

Потенциальная энергия тела, поднятого на высоту h, равна

где 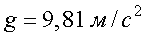- ускорение свободного падения.

Потенциальная энергия упруго сжатой пружины равна

где k - коэффициент упругости, 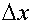- деформация (изменение длины тела).

Работа в потенциальном поле сил равна убыли потенциальной энергии:

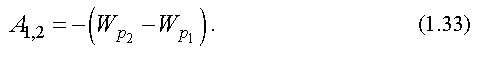
Соударение двух тел

Рассмотрим два примера на применение законов сохранения импульса и энергии при соударении двух тел. Существует два предельных вида удара: абсолютно упругий и абсолютно неупругий.

ЭЛЕКТРОМАГНЕТИЗМ

Это раздел физики, изучающий все электромагнитные взаимодействия.

Электростатика

Электростатика изучает взаимодействие неподвижных электрических зарядов и свойства постоянного электрического поля.

Постоянный ток

В этом разделе изучается направленное движение электрических зарядов.

Сила и плотность тока

Основной характеристикой тока является сила тока.

Силой тока называется скалярная величина, равная отношению величины заряда, протекающего через поперечное сечение проводника за некоторый интервал времени, к величине этого интервала.

Для постоянного тока, т. е. тока, не изменяющегося со временем, справедлива следующая формула

В общем случае, если ток переменный, то сила тока вычисляется как производная от заряда по времени:

Плотностью тока называется вектор, величина которого равна отношению силы тока, протекающего через элементарную площадку, перпендикулярную направлению движения зарядов, к площади этой площадки:

Единица плотности тока - 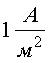. Вектор плотности тока направлен в сторону движения положительных электрических зарядов.

Плотность тока может быть выражена через концентрацию носителей заряда n и среднюю скорость их упорядоченного движения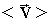

где e - заряд одного носителя.

Объяснение закона Ома

Задача физики - выяснить природу явлений, описываемых физическими законами.

Для объяснения закона Ома (2.28) в начале XIX в. была разработана классическая теория электропроводности металлов. Согласно классическим представлениям, электроны проводимости в металлах образуют так называемый электронный газ. Подобно молекулам идеального газа электроны в металле участвуют в хаотическом движении. При приложении электрического поля на хаотическое движение электронов накладывается упорядоченное движение. Среда оказывает сопротивление движению зарядов в определенном направлении. Поэтому в однородном веществе при постоянной напряженности поля 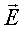заряды движутся с постоянной скоростью 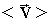, пропорциональной напряженности поля

где μ - подвижность носителей, которая зависит от природы носителей, плотности и состояния вещества.

Подставим формулу (2.29) в (2.23) и получим закон Ома в дифференциальной форме

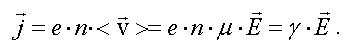
Основанная на этих представлениях классическая теория электропроводности помогла понять и объяснить ряд физических явлений. Но следует отметить, что некоторые экспериментальные факты (например, сверхпроводимость металлов, зависимость сопротивления от температуры, значение их теплоемкости и др.) можно объяснить только с помощью квантовой теории. Однако, классическая теория электропроводности не утратила своего значения и в наши дни, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре, как это имеет место для полупроводников) она дает правильные результаты.

Магнетизм

Это раздел физики, изучающий магнитные явления.

Магнитное поле прямого тока

Применяя закон Био - Савара - Лапласа и принцип суперпозиции, можно найти напряженность магнитного поля прямого тока. Запишем без вывода конечный результат для проводника конечной длины (рис. 2.13).

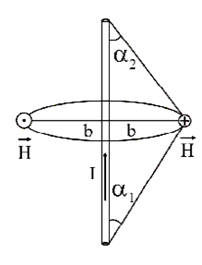
Рис.2.13

Введем следующие обозначения: I - сила тока в проводнике, b - кратчайшее расстояние от точки наблюдения до проводника, α₁ и α₂ - углы между отрезком проводника и линией, соединяющей концы отрезка с точкой наблюдения.

Напряженность магнитного поля, созданного конечным прямым проводником с током, равна

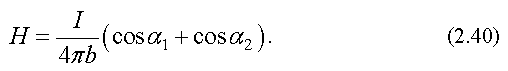
Направление вектора 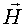определяется по правилу правого винта. Вектор, направленный за чертеж, изображается крестиком 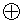. Вектор, направленный к нам - точкой . Линия напряженности представляет собой окружность.

Для бесконечно длинного проводника 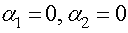и 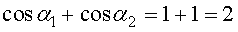. Напряженность магнитного поля равна

Модуль вектора магнитной индукции, соответственно, равен

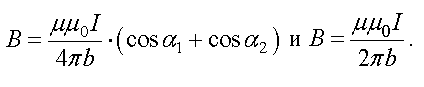
Сила Лоренца. Сила Ампера

Магнитное поле не только порождается движущимися электрическими зарядами, но действует на движущиеся заряды.

Силой Лоренца называется сила, действующая на движущийся электрический заряд со стороны магнитного поля. Сила Лоренца равна произведению заряда q на векторное произведение скорости движения заряда 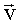и вектора магнитной индукции 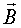, т. е.

Модуль силы Лоренца равен

где α - угол между векторам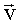и и .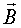

Поскольку ток - это упорядоченное движение электрических зарядов, то на проводник с током в магнитном поле тоже действует сила, которая называется силой Ампера.

Сила Ампера равна произведению силы тока на векторное произведение элемента проводника 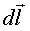и вектора магнитной индукции

Модуль силы Ампера равен

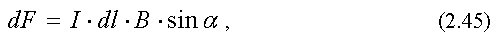
где α - угол между векторами .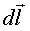

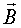С помощью измерения силы можно найти модуль вектора магнитной индукции (формула (2.45)). Сила будет максимальной, если sinα = 1. Тогда по формуле (2.45)

.

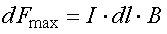Отсюда:

.

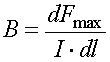Тогда единица магнитной индукции тесла (Тл) равна ньютон (Н), деленный на ампер и на метр , т. е.

.

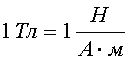КОЛЕБАНИЯ И ВОЛНЫ

В этом разделе изучаются повторяющиеся процессы и распространение колебаний в пространстве.

Колебания

Векторная диаграмма

При рассмотрении многих вопросов, в частности, при сложении колебаний одинакового направления и частоты бывает удобно гармоническое колебание представить в виде векторной диаграммы. Векторная диаграмма строится следующим образом: надо изобразить вектор, длина которого равна амплитуде, угол наклона к оси абсцисс равен начальной фазе. Если привести этот вектор во вращение с угловой скоростью ω₀, равной круговой частоте колебаний, то проекция его конца на выбранную ось будет изменяться по гармоническому закону.

На рис. 3.3 представлена векторная диаграмма для гармонического колебания

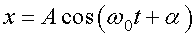
в момент времени t = 0.

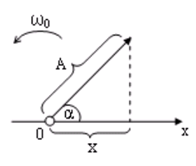
Рис.3.3

Метод векторных диаграмм удобен при сложении колебаний одинаковой частоты.

Волны

Волновые процессы

Волной называется процесс распространения колебаний или других возмущений в пространстве.

Основными видами волн являются механические упругие волны, волны на поверхности жидкости и электромагнитные волны.

Упругими волнами называются волны, которые могут распространяться в упругой среде (т. е. среде, которая сопротивляется сжатию: твердой, жидкой и газообразной). К ним относятся, в частности, ударные, звуковые и сейсмические волны. Упругие волны называют также механическими волнами.

Электромагнитные волны могут распространяться как в среде, так и в вакууме (например, радиоволны, световые волны).

Характерным свойством волн является перенос энергии без переноса вещества. Например, по некошенному полю пшеницы от порывов ветра распространяется волна. При этом колосья колеблются около своих положений равновесия, а волна идет по всему полю.

Рассмотрим этот процесс более подробно. Частицы среды, в которой распространяется волна, колеблются около своих положений равновесия. В зависимости от направления колебаний частиц среды по отношению к направлению распространения волны различают волны продольные и поперечные.

В продольной волне частицы колеблются вдоль направления распространения волны, в поперечной волне колебания частиц совершаются перпендикулярно направлению распространения волны. В жидкой и газообразной среде возможно распространение только продольных волн, в твердой среде - как продольных, так и поперечных.

Энергия упругой волны

Распространение волн связано с переносом энергии. При этом частицы среды не переносятся волной, а совершают колебание около положения равновесия. Скорость колеблющейся частицы, в соответствии с формулами (3.11) и (3.24), равна

.

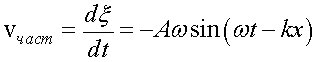Кинетическая энергия частиц, заключенных в объеме 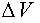, равна (см. формулу (1.29))

.

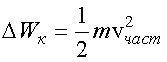Масса выделенного объема m равна

,

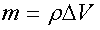где ρ - плотность среды.

Тогда значение кинетической энергии выделенного объема равно

.

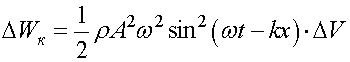Выделенный объем обладает также потенциальной энергией 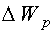. Можно показать, что

,

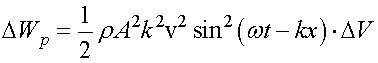где, согласно формуле (3.23), .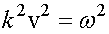

Следовательно, кинетическая энергия выделенного объема равна потенциальной энергии.

Полная энергия равна сумме кинетической и потенциальной энергии

.

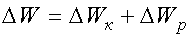Полная энергия, возникающая в упругой среде при распространении в ней плоской гармонической волны, равна

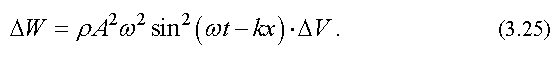
Плотностью энергии называется энергия, заключенная в единице объема, т. е.

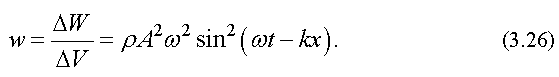
Из формулы (3.26) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. Среднее значение плотности энергии определяется средним значением квадрата синуса

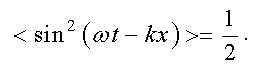
Следовательно, среднее по времени значение плотности энергии в данной точке среды равно

Итак, энергия волны (3.25), плотность энергии (3.26) и ее среднее значение (3.27) пропорциональны плотности среды, квадрату амплитуды и квадрату частоты.

Электромагнитные волны

Электромагнитными волнами называется процесс распространения в пространстве переменного электромагнитного поля. Теоретически существование электромагнитных волн предсказано английским ученым Максвеллом в 1865 г., а впервые они экспериментально получены немецким ученым Герцем в 1888 г.

Из теории Максвелла вытекают формулы, описывающие колебания векторов 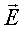и 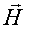. Плоская монохроматическая электромагнитная волна, распространяющаяся вдоль оси x, описывается уравнениями

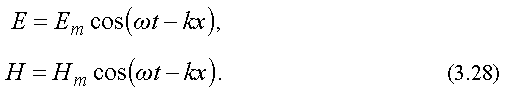
Здесь E и H - мгновенные значения, а E_m и H_m - амплитудные значения напряженности электрического и магнитного полей, ω - круговая частота, k - волновое число. Векторы 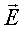и 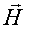колеблются с одинаковой частотой и фазой, взаимно перпендикулярны и, кроме того, перпендикулярны вектору 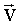- скорости распространения волны (рис. 3.7). Т. е. электромагнитные волны поперечны.

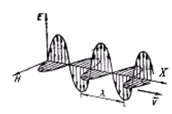
Рис.3.7

В вакууме электромагнитные волны распространяются со скоростью 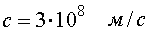. В среде с диэлектрической проницаемостью ε и магнитной проницаемостью µ скорость распространения электромагнитной волны равна:

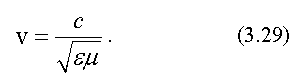
Частота электромагнитных колебаний, так же, как и длина волны, могут быть в принципе любыми. Классификация волн по частоте (или длине волны) называется шкалой электромагнитных волн. Электромагнитные волны делятся на несколько видов.

Радиоволны имеют длину волны от 10³ до 10^-4 м.

Световые волны включают:

· инфракрасное излучение,

· видимый свет в интервале ,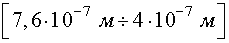

· ультрафиолетовое излучение.

Рентгеновское излучение - .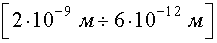

Гамма-излучение имеет длину волны < 10^-12 м.

Световые волны

Световые волны - это электромагнитные волны, которые включают в себя инфракрасную, видимую и ультрафиолетовую части спектра. Длины световых волн в вакууме, соответствующие основным цветам видимого спектра, указаны в нижеприведенной таблице. Длина волны дана в нанометрах, .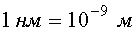

Таблица

Цвет	Длина волны, нм	Цвет	Длина волны, нм
красный	760 - 620	голубой	510 - 480
оранжевый	620 - 590	синий	480 - 450
желтый	590 - 575	фиолетовый	450 - 380
зеленый	575 - 510

Для световых волн характерны те же свойства, что и для электромагнитных волн.

1. Световые волны поперечны.

2. В световой волне колеблются вектора 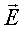и .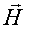

Опыт показывает, что все виды воздействий (физиологическое, фотохимическое, фотоэлектрическое и др.) вызываются колебаниями электрического вектора 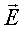. Его называют световым вектором. Уравнение световой волны имеет сведующий вид

Амплитуду светового вектора E_m часто обозначают буквой A и вместо уравнения (3.30) используют уравнение (3.24).

3. Скорость света в вакууме .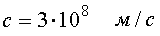

Скорость световой волны в среде определяется по формуле (3.29). Но для прозрачных сред (стекло, вода) обычно 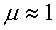, поэтому .

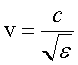Для световых волн вводится понятие - абсолютный показатель преломления.

Абсолютным показателем преломления называется отношение скорости света в вакууме к скорости света в данной среде

Из (3.29), с учетом того, что для прозрачных сред 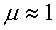, можно записать равенство .

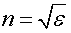Для вакуума ε = 1 и n = 1. Для любой физической среды n > 1. Например, для воды n = 1,33, для стекла 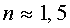. Среда с большим показателем преломления называется оптически более плотной. Отношение абсолютных показателей преломления называется относительным показателем преломления:

4. Частота световых волн очень велика. Например, для красного света с длиной волны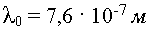

.

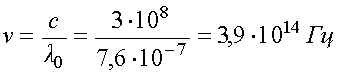При переходе света из одной среды в другую частота света не изменяется, но изменяется скорость и длина волны.

Для вакуума - 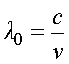; для среды - 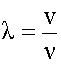, тогда

.

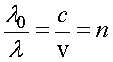Отсюда длина волны света в среде равна отношению длины волны света в вакууме к показателю преломления

5. Поскольку частота световых волн очень велика 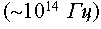, то глаз наблюдателя не различает отдельных колебаний, а воспринимает усредненные потоки энергии. Таким образом вводится понятие интенсивности.

Интенсивностью называется отношение средней энергии, переносимой волной, к промежутку времени и к площади площадки, перпендикулярной направлению распространения волны:

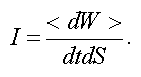
Поскольку энергия волны пропорциональна квадрату амплитуды (см. формулу (3.25)), то интенсивность пропорциональна среднему значению квадрата амплитуды

Характеристикой интенсивности света, учитывающей его способность вызывать зрительные ощущения, является световой поток - Ф.

6. Волновая природа света проявляется, например, в таких явлениях, как интерференция и дифракция.

Задания и вопросы для самоконтроля

1. Что называется волной? Приведите примеры волн.

2. Что называется фронтом волны? Волновой поверхностью?

3. Назовите характеристики волнового процесса и дайте их определения.

4. Как получить уравнение плоской волны?

5. От чего зависит энергия и плотность энергии волн?

6. Что такое электромагнитная волна? Какова скорость ее распространения?

7. Что представляет собой шкала электромагнитных волн?

8. Что называется световым вектором?

9. Дайте определение абсолютного и относительного показателей преломления.

10. Что называется интенсивностью?

Волновая оптика

Явление интерференции света

Волны, как и колебания, могут складываться. Сложение волн может быть интерференционным и неинтерференционным. Интерференцией называется сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны, не изменяющееся с течением времени. Интерференция наблюдается только от когерентных источников. Когерентность - значит согласованность. Когерентными источниками называются такие источники, которые дают волны одинаковой частоты, и для фиксированной точки пространства разность фаз колебаний остается постоянной.

Независимые источники света не могут быть когерентными, так как в каждом из них свет испускается множеством атомов, излучающих несогласованно. Разность фаз колебаний, испускаемых совокупностью атомов таких источников, быстро и беспорядо<