Дифракция Фраунгофера на круглом отверстии

В этом случае дифракционная картина представляет собой чередование светлых и тем­ных колец. Распределение интенсивности задается функцией:

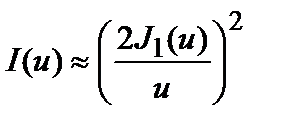. (3.30.12)

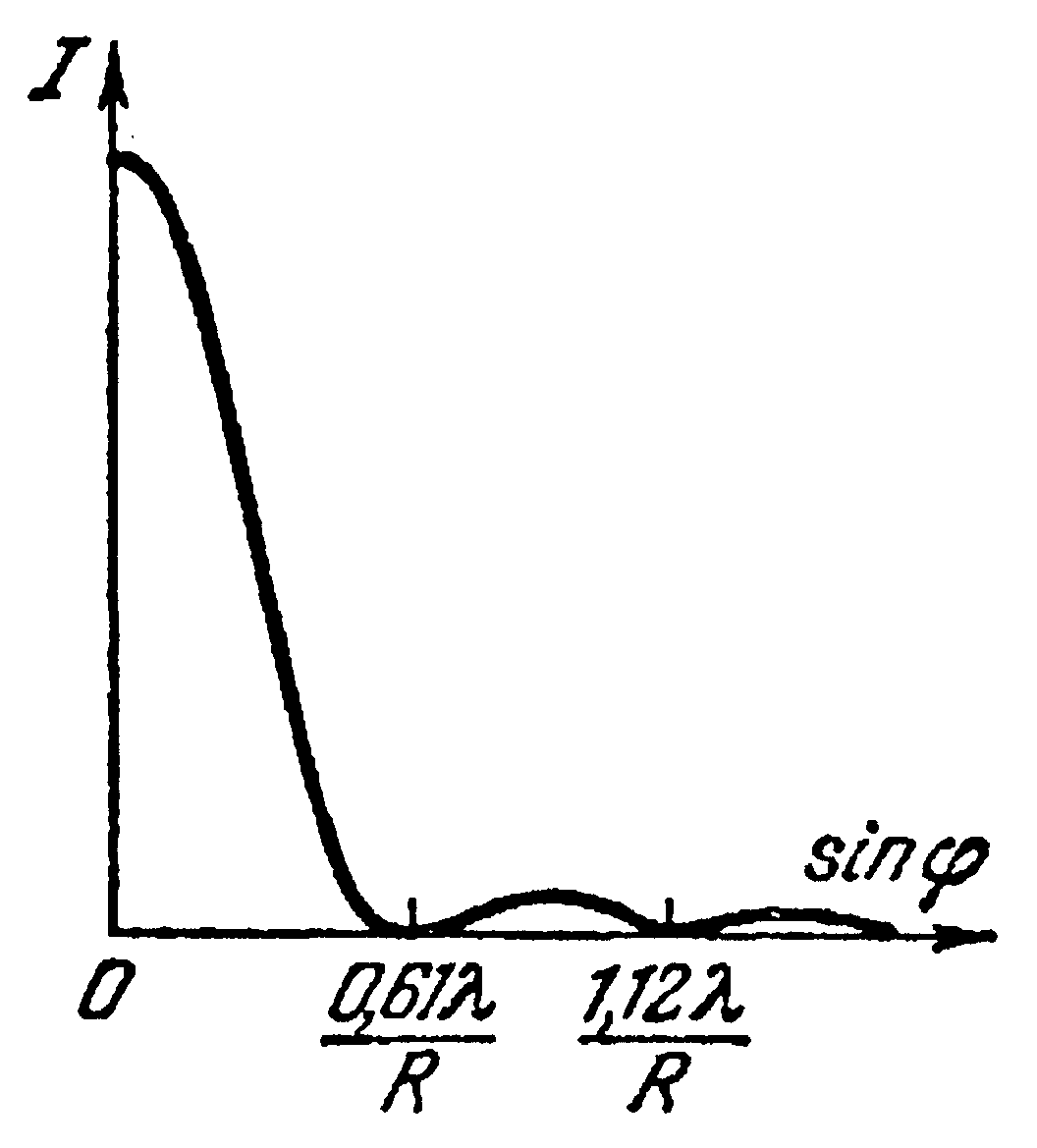
Расчет положения минимумов и максимумов в математическом плане сводится к определению корней функции Бесселя J₁(u):

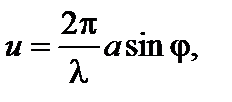(3.30.13)

где а – радиус отверстия.

Рис. 3.30.6.

Положение максимумов и минимумов удовлетворяют условию

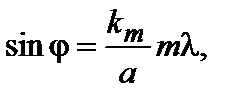(3.30.14)

где т = 1, 2, 3, 4, ... – порядок максимума или минимума. Значения k_мин, k_мах и относи­тельные интенсивности максимумов I_отн для т = 1, 2, 3, 4приведены в таблице.

m	kмах	kмин	Iотн
		0,61
	0,41	0,56	0,0175
	0,44	0,54	0,0042
	0,46	0,53	0,0016

ПРИМЕРЫ ДИФРАКЦИОННЫХ КАРТИН

Пятно Пуассона

Рис. 3.30.7.

• Дифракция на дисках различного диаметра приводит к появлению в центре геометрической тени максимума – т.н. пятна Пуассона.

• Диаметр и яркость пятна увеличиваются при уменьшении диаметра диска.

Дифракция Френеля на круглом отверстии

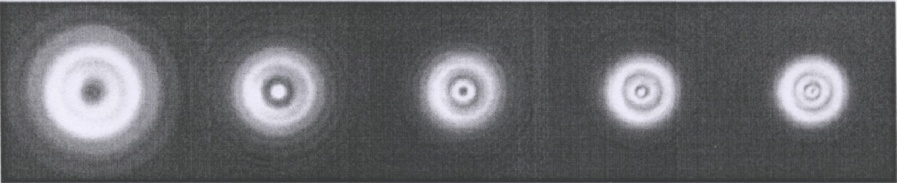
Рис. 3.30.8.

• Дифракция Френеля на круглом отверстии по мере приближения к экрану с отверстием.

• Число открытых полуволновых зон увеличивается слева направо с 2 до 6.

• Размер картины уменьшается, приближаясь к диаметру отверстия.

Дифракция Френеля на щели

Рис.3.30.9.

• Одномерная дифракция Френеля на вертикальной щели по мере ее расширения.

• Начальная ширина соответствует примерно одной открытой полуволновой зоне, конечная – пяти открытым зонам.

• Вертикальный размер картины определяется диаметром пучка, падающего на щель.

Границы дифракционных приближений

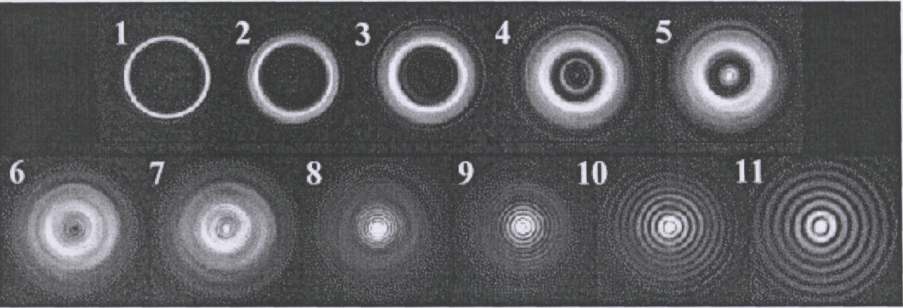
Рис.3.30.10.

• На примере дифракции на кольце можно проследить плавный переход от геометриче­ской оптики (1-3) через дифракцию Френеля (4-7) к дифракции Фраунгофера (9-11).

• Число открытых зон т уменьшается слева направо, при этом значение т = 1 (дистан­ция Рэлея, условная граница между дифракциями Френеля и Фраунгофера) соответст­вует снимку 8.

Дифракция Фраунгофера на щели

Рис. 3.30.11.

• Одномерная дифракция Фраунгофера на вертикальной щели по мере ее расширения слева направо.

• Нулевой максимум наиболее яркий и вдвое шире побочных максимумов.

• Размер области дифракционного расплывания обратно пропорционален ширине щели.

ОПИСАНИЕ ОБОРУДОВАНИЯ

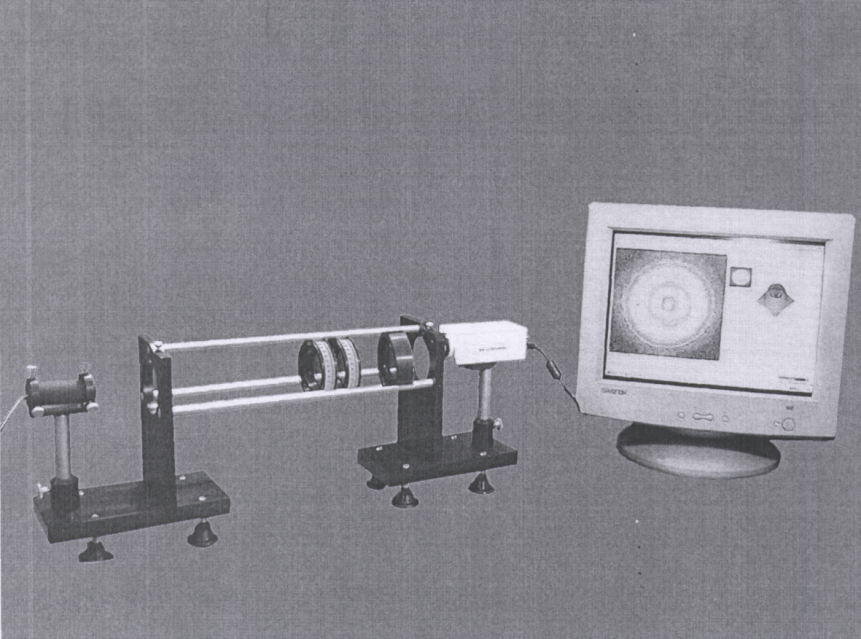
Градуировка системы

Координатные измерения на изображении производятся в пикселях с помощью программы OSC WDM. Размер одного пикселя матрицы OV-9121 камеры VAK-135 составляет 5,2 5,2 мкм. При формате видеоизображения 1280 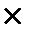1024 изображение воспроизводится в масштабе 1:1.

При использовании объектива следует провести подобную калибровку, разместив в поле зрения объектива объект с известными геометрическими размерами. При этом следует иметь в виду, что из-за дисторсии объектива масштабный коэффициент может меняться по полю зрения (в особенности для короткофокусных объективов).

Настройка АРМС

Включите питание лазерного излучателя.

Поверните поляризатор так, чтобы пятно лазера было хорошо заметно на объекте.

На юстировочном модуле лазера имеются два кольца, в каждое из которых вкручены по три винта. Отжимая и вкручивая винты, необходимо добиться того, чтобы лучи отраженные от поляризатора и объекта попали на выходную диафрагму лазера. В этом случае пучок, излучаемый лазером перпендикулярен поверхностям поляризатора и объекта.

Порядок измерений

1. Видеокамера должна быть подключена к компьютеру. Изображение строится непосредственно на матрице камеры, поэтому с камеры надо снять крышку (камера должна быть без объектива).

Запустите программу OSC WDM (иконка на рабочем столе).

Драйвер giveio.sys для работы в комплекте АРМС не требуется. Если программа не запускается, отсоедините и через 5 секунд снова присоедините разъем USB2, подключающий камеру к системному блоку.

2. Если конфигурация настройки программы ранее была изменена, то в меню «Настройка» основного окна выберите п. «Чтение параметров» и загрузите файл настройки.

Рекомендуемая конфигурация записана в файле «ARMS7.pdt». Вы можете в последующем создать несколько файлов конфигураций для решения различных задач и выбирать необходимый.

3. Активируйте окно «График по X», затем установите режим захвата изображений нажатием кнопки

Вызовите закладку «Video Capture Filter» и установите необходимые режимы работы видеокамеры:

• Saturation – 0

• Sharpness – 0

• Backlight – 0

• Exposure – Manual (Auto – выкл.)

4. Выберите на объекте МОЛ требуемую структуру и направьте на нее пучок лазера. Для этого отожмите винт рейтера и поднимая или опуская стойку с камерой вверх-вниз, выберите нужный ряд структур на объекте МОЛ и, вращая объект вокруг оптической оси, получите на мониторе изображение дифракционной картины.

5. Установите коэффициент усиления (движок Exposure – Manual), обеспечивающий яркое, контрастное изображение. Вращением поляризатора скорректируйте интенсивность пучка лазера. Для более точной настройки можно использовать используйте экранную лупу. Поляризатором подстройте амплитуду, так чтобы центральный максимум был наибольшим, но не происходило перезасвечивания (насыщения) ПЗС-матрицы. Признаком насыщения является ровный белый фон участка изображения, значения интенсивности в этой зоне в окне «График по X» равно 255. Таким образом, измеряемый уровень интенсивности всегда должен быть меньше 255. В дальнейшем, если измерения будут проводиться на дифракционных максимумах высоких порядков, то допускается перезасвечивание центрального максимума, как показано на рис. 3.30.15.

6. При работе с высоким уровнем шумов следует установить в программе большее число кадров для суммирования в режиме накопления (рекомендуемое значение 50). Для проведения измерения следует включить режим накопления нажатием кнопки .

Зафиксировать изображение можно нажатием кнопки «Стоп-кадр накопленного изображения с обработкой» .

Зафиксированное изображение при необходимости сохранить в виде графического файла нажатием кнопки «Запись файла изображения».

Описанные ниже действия могут выполняться как на зафиксированном изображении, так и на сохраненном ранее и вызванном нажатием кнопки «Чтение файла изображения».

7. Идентификация номера структуры на объекте производится следующим образом (на примере ряда С объекта МОЛ-1).

Внешний вид объекта МОЛ-1 приведен на рис. 3.30.9 (более подробное описание см. Приложение 1).

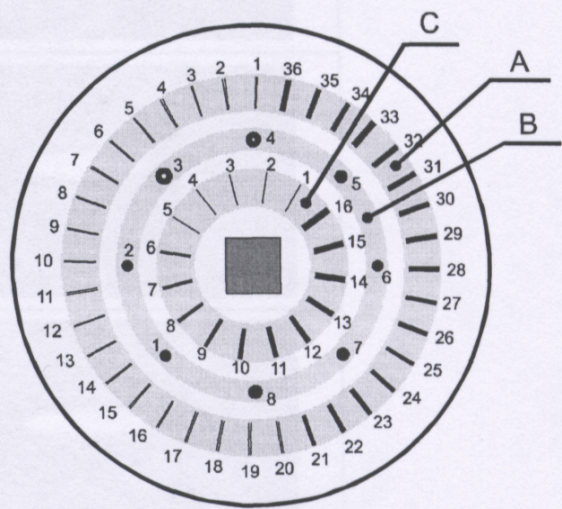
Рис. 3.30.12. Схема расположения структур объекта МОЛ-1 (Ряд С одинарные щели толщины d (в мкм) в порядке возрастания номера: 8; 10; 12; 15; 20; 25; 30; 35; 40; 45; 50; 60; 70; 80; 90; 100.

После получения изображения дифракционной картины следует вращением объекта МОЛ-1 вокруг оптической оси получить последовательно ряд изображений, как показано на рис. 4. Начало отсчета в нумерации структур следует установить по переходу от изображения 1 к изображению 16 (рис. 10). Далее следует визуальный контроль числа дополнительных дифракционных максимумов для структур 1 .. 16 , визуализируемых на экране монитора, изменяя при необходимости уровень усиления и накопления. Допускается перенасыщение изображения центрального максимума.

№ структуры ряда С	Дифракционная картина	№ структуры ряда С	Дифракционная картина

Рис. 3.30.13. Дифракционные изображения от структур №№ 1-16 ряда С объекта МОЛ-1.

8. Выберите и зафиксируйте на изображении опорную точку нажатием кнопки «Установка опорной точки» (например, основной максимум или минимум дифракционной картины). Точную подстройку положения перекрестья при выборе точки можно произвести с помощью кнопок

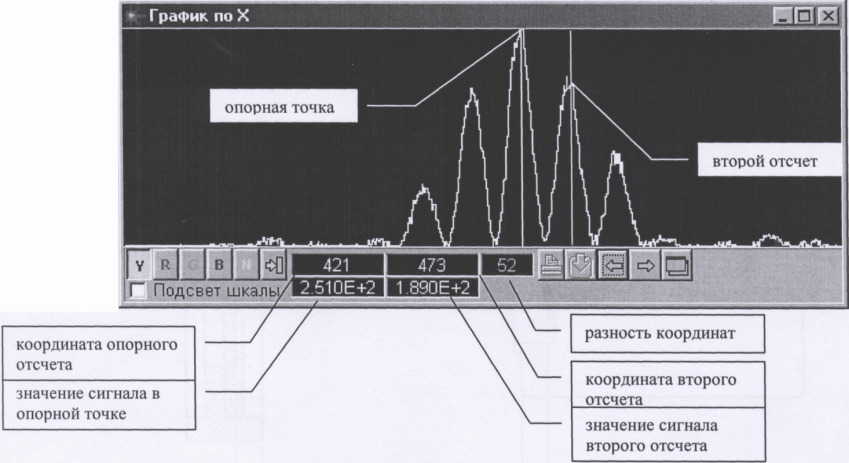
Рис. 3.30.14. Общий вид окна «График по Х».

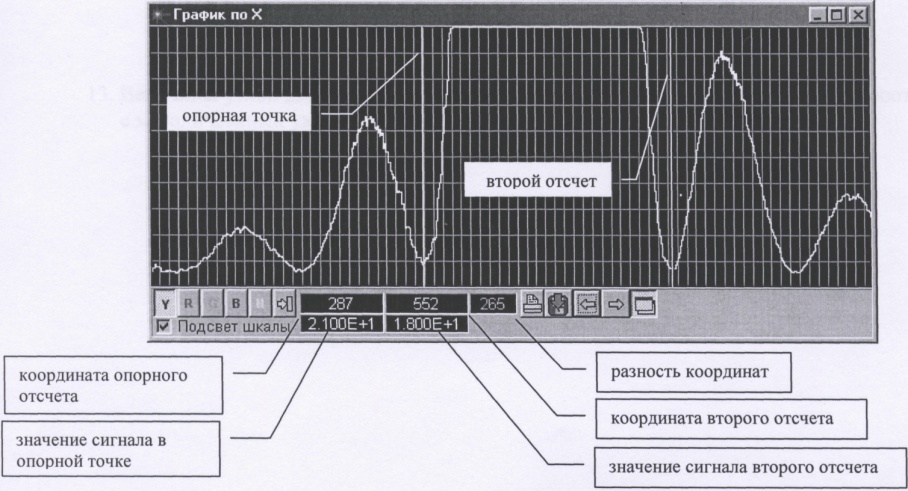
Рис. 3.30.15. Координатные измерения в окне «График по Х»

программы OSC WDM

9. В любом из окон с графиками щелкните левой кнопкой мыши в месте, где производится второй отсчет (соседний максимум или минимум дифракционной картины). Более точную подстройку положения перекрестья можно произвести с помощью кнопок

ориентируясь на величину амплитуды.

10. Разность между двумя отсчетами (см. рис. 3.30.15) в пикселях необходимо перевести в миллиметры. Для этого число пикселей умножаем на масштабный коэффициент, определенный при градуировке. Уровни сигналов в точках отображаются в соответствующих окнах. Диапазон измеряемых сигналов 0 ... 255.

11. Полученный график можно распечатать на принтере либо сохранить в виде текстового файла значений сигнала для последующей обработки другими программами, например средствами Microsoft Excel.

12. Расстояние между матрицей камеры и поверхностью объекта, необходимое для расчетов определяется следующим образом:

1) Измерить с помощью линейки расстояние D (см. рис. 3.30.16) между торцевыми поверхностями оправы, в которой закреплен объект, и видеокамеры

2) Вычислить расстояний L по формуле L = 7мм + D + 11мм + dn, где d – толщинапокровного стекла ПЗС-матрицы, n – показатель преломления стекла (в расчете принять d = 1 мм, n = 1,5).

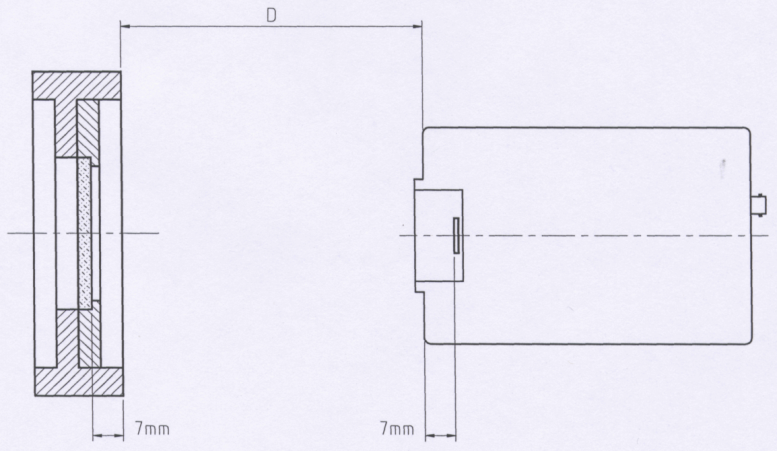
Рис. 3.30.16. Определение расстояния между матрицей камеры VAC-135 и поверхностью объекта.

Обработка результатов

Задание 1. Величины углов дифракции для щели с заданной шириной рассчитываются из геометрических измерений в соответствии с методическими указаниями и сравниваются с теоретическими данными.

Задание 2. Используя формулу (3.30.2) и полученные значения 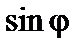рассчитайте ширину некоторой щели для порядков спектра k = 1, 2, 3. Длина волны излучения лазера .

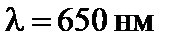Контрольные вопросы

1. Какая картина возникает при дифракции света на одной щели?

2. Какая картина возникает при дифракции света на двух одинаковых параллельных щелях?

3. Какая картина возникает при дифракции Фраунгофера на круглом отверстии?

4. Как определить ширину щели с помощью дифракции?

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики: Учеб пособие для втузов. – М: Высш. Шк., 1989. – 608 с.

2. Савельев И.В. Курс общей физики. Т.2.Учеб. пособие для студентов втузов. – М.: КНОРУС, 2009, 576 с.

3. Трофимова Т.И. Курс физики. Учеб. пособ. для вузов.- 15-е изд., стереотип. – М.: Издательский центр «Академия», 2007. –560 с.

4. Калитеевский Н.И. Волновая оптика. Учеб. пособ. для вузов.- 3-изд., перераб. и доп.. – М.: Высш. шк., 1995. – 463 с.