Изменение энтропии в некоторых процессах

Во всех процессах, сопровождающихся хаотизацией структуры системы (плавление кристаллов, испарение жидкостей, расширение газов, смешение и растворение, химические реакции разложения), происходит увеличение энтропии.

В обратных им процессах (кристаллизация, конденсация паров, сжатие газов, процессы мембранного разделения, химические реакциии синтеза), где порядок расположения элементов системы возрастает, происходит уменьшение энтропии.

Рассмотрим несколько примеров расчета энтропии для типичных термодинамических систем и процессов.

В отличие от H и U можно определять абсолютные значения S для всех чистых веществ при любой температуре. Для вычисления стандартных энтропий веществ важное значение имеет третий закон (начало) термодинамики, сформулированный В. Нернстом (теорема Нернста, 1906 г.) и М. Планком (постулат Планка, 1911 г.).

Третье начало гласит, что при стремлении температуры к нулю энтропия для равновесных состояний также стремится к нулю, хотя достижение такого состояния невозможно из-за квантовой природы движения и запрещено соотношением неопределенностей Гейзенберга. Любое вещество имеет определенную положительную энтропию, но при абсолютном нуле энтропия чистых веществ, существующих в виде идеальных кристаллов, равна нулю. В соответствии с уравнением Больцмана при температуре, стремящейся к абсолютному нулю
(Т → 0 К), W = 1 (единственно возможное макросостояние – идеально правильно построенный кристалл) и S = 0. В реальных кристаллах всегда имеются дефекты структуры, поэтому значение S для них даже при 0 К должно быть больше нуля. Фактически численные значения «нулевой энтропии» S реальных кристаллов столь малы, что не мешают составить таблицы абсолютных значений стандартных энтропий веществ S⁰₂₉₈ [Дж/мольК] (газы, жидкости, стеклообразные фазы и растворы не подчиняются третьему началу термодинамики).

Стандартные энтропии чистых веществ относят к 1 молю вещества при р = 101 кПа и Т = 298 К и обозначают S⁰₂₉₈[Дж/моль×К]. Стандартные энтропии простых веществ положительны и не равны нулю. Стандартная энтропия образования соединения ∆_fS⁰₂₉₈ равна изменению энтропии в ходе реакции образования 1 моля соединения в стандартных условиях из простых веществ в стандартном состоянии. В ряду однотипных соединений энтропия растет по мере усложнения атомов, входящих в состав молекул, а также по мере усложнения состава молекул. Стандартные значения энтропии веществ S⁰₂₉₈ приведены в термодинамических справочниках.

Поскольку энтропия есть функция состояния, то её изменение ∆S, сопровождающее химическую реакцию, можно рассчитать аналогично изменению энтальпии. Для химической реакции в стандартных условиях

∆S⁰_{298 (реакции)} = ∑(n'S⁰₂₉₈)_прод.− ∑(n''S⁰₂₉₈)_исх.,

где n', n'' – соответствующие стехиометрические коэффициенты в уравнении реакции.

Энтропия является возрастающей функцией температуры, причем особенно резко, скачкообразно она изменяется при температурах фазовых переходов. Изменение энтропии (∆S_i) при фазовых превращениях (плавление↔кристаллизация – D_mH; испарение↔конденсация – D_vH; полиморфные превращения кристаллов) можно рассчитать:

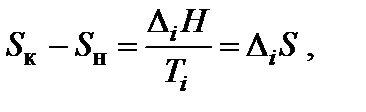
где D_iH и T_i – соответственно энтальпия и температура фазового перехода.

Вообще для любого обратимого процесса при постоянных р, T, когда известна величина ∆H, изменение энтропии

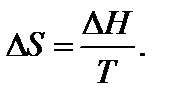
Температура является характеристикой (мерой) теплового движения молекул и атомов. Поэтому с ростом температуры растет интенсивность движения частиц и соответственно уменьшается упорядоченность системы, следовательно, возрастает энтропия:

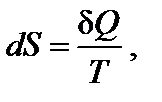
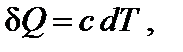
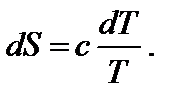
При нагревании в изобарных условиях (р = const) изменение энтропии (если есть фазовые переходы)

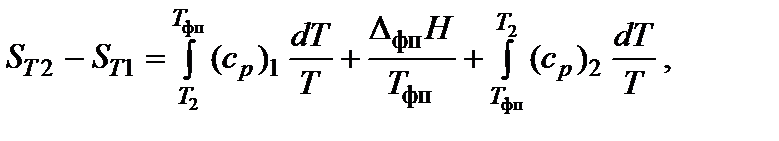
где Т₁ и Т₂ – температурный интервал, Т_фп – температура фазового перехода, D_фпH – энтальпия фазового перехода, (с_р)_i – изобарная теплоемкость соответствующей фазы.

3.3. Направленность самопроизвольных процессов.
Свободная энергия Гиббса

Критерием направленности самопроизвольных процессов при р, Т = const, учитывающим энтальпийную и энтропийную составляющие движущей силы процесса, является изменение термодинамической функции состояния (∆G), называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса.

Из предыдущего раздела ( 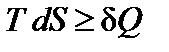) следует, что первое начало термодинамики можно представить в виде

dU + p dV – T dS £ 0,

где знак равенства относится к условию состояния термодинамического равновесия системы, а знак неравенства – к условию самопроизвольного протекания неравновесного процесса.

Рассмотримизобарно-изотермический процесс(p = const, Т = const). Поскольку dQ_p = dH = dU + pdV, то dH – TdS £0. При постоянной температуре d(H – T S)£0. Выражение под знаком дифференциала заменяется функцией G º H – T×S. Тогда очевидно, что условием самопроизвольного протеканияизобарно-изотермического процесса будет dG <0 (DG <0), а условием равновесия dG =0 (DG =0).

G – функция состояния системы, получившая название энергии Гиббса или изобарно-изотермического потенциала. Энергия Гиббса – часть энергии системы, которая может быть отдана ею в изобарно-изотермическом процессе в виде теплоты или работы без разрушения самой системы. Таким образом, термодинамическое условие самопроизвольного протекания реакции:

∆G <0 или ∆H – T∆S <0.

Неравенства определяют принципиальную возможность течения химической реакции при постоянных р, T. Для реального осуществления процесса необходимы не только выполнение термодинамических условий, но и учет кинетических факторов.

Процесс принципиально невозможен, если ∆G >0. Чем более отрицательно значение ∆G, тем более реакционноспособна система. Изменение энергии Гиббса отражает влияние на направление протекания процесса энтальпийного (∆Н) и энтропийного (T∆S) факторов. В зависимости от температуры влияние одного из этих факторов на значение и знак ∆G может быть определяющим.

Химические реакции можно классифицировать по возможности и условиям протекания в зависимости от характера изменения ∆Н и ∆S.

1. В изолированных системах ∆Н = 0, тогда неравенство
∆H – T ∆S <0 принимает вид − T ∆S <0. Развитие любого самопроизвольного процесса обусловлено только энтропийным фактором
∆S >0.

2. В неизолированных системах при высоких температурах критерием осуществимости процесса является изменение энтропии
(∆S >0). Энтропийный фактор влияет на направление процессов растворения кристаллических веществ, идущих с поглощением теплоты (∆Н > 0). В данном случае ∆S >> 0 и |T ∆S| >> |∆Н|, следовательно,
∆G ≈ −T ∆S и ∆G <0.

При низких температурах для реакций со значительным тепловым эффектом |∆Н| >> |T ∆S| и ∆G ≈ ∆H. Следовательно, ∆G < 0, если ∆Н < 0 (∆S > 0 или ∆S <0). При низких температурах возможность самопроизвольного протекания реакции определяется изменением энтальпии (∆Н <0).

Для большинства реакций, идущих при обычной температуре и атмосферном давлении, |∆Н |> |T ∆S|, поэтому в этих условиях эндотермические реакции (∆Н >0) редко протекают самопроизвольно в отличие от экзотермических (∆Н <0).

Изменение изобарно-изотермического потенциала в ходе химической реакции определяется следующим образом:

∆G_{T (реакции)} = ∆H_{T (реакции)} − T∆S_{T (реакции)}

или, аналогично выражению для ∆H (реакции), так как G – функция состояния:

∆H⁰_{298 (реакции)} = ∑(n'∆_fH⁰₂₉₈)_прод − ∑(n''∆_fH⁰₂₉₈)_исх

∆G_{(реакции)}= ∑n' ∆_fG_(прод) – ∑n'' ∆_fG_(исх) .

Если значение ∆G реакции определяют в стандартных условиях, уравнение принимает вид

∆G⁰_{298(реакции)} = ∑n' ∆_fG⁰_{298(прод)} −∑n'' ∆_fG⁰_298(исх) ,

где ∆_fG⁰₂₉₈ – стандартный изобарный потенциал образования соединения, равный изменению изобарного потенциала реакции образования 1 моля этого соединения при стандартных условиях из простых веществ в стандартном состоянии.

Эта величина выражается в килоджоулях на моль (кДж/моль). Для простых веществ ∆_fG⁰₂₉₈ = 0. Значение ∆_fG⁰₂₉₈ определяется как

∆_fG⁰₂₉₈ = ∆_fH⁰₂₉₈ − T ∆_fS⁰₂₉₈ .

Пределом убыли свободной энергии Гиббса при самопроизвольном протекании процесса является ее минимальное значение, отвечающее состоянию равновесия. Такое состояние системы наиболее устойчиво, всякое отклонение от него требует затраты энергии.

Термодинамическим условием состояния равновесия является равенство:

∆G = 0 или ∆H − T ∆S = 0 .

Пренебрегая зависимостью ∆Н и ∆S от температуры, можно приближенно определить температуру наступления химического равновесия:

T_равн = ∆H⁰₂₉₈ /∆S⁰₂₉₈ .

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Пример 1. Определить тепловой эффект процесса термического разложения хлорида аммония и составить термохимическое уравнение реакции.

Решение. Реакция выражается уравнением NH₄Cl(к) → NH₃(г) + + HCl(г). Согласно следствию из закона Гесса

∆H⁰_{298 (реакции)} = ∑(n'∆_fH⁰₂₉₈)_прод− ∑(n''∆_fH⁰₂₉₈)_исх =

= ∆H⁰₂₉₈(NH₃)(г) + ∆H⁰₂₉₈(HCl)(г) - ∆H⁰₂₉₈(NH₄Cl)(к).

Используя справочные данные значений ∆H⁰₂₉₈веществ, получаем

∆H⁰_{298(реакции)} = (-46,2 – 92,2) – (-314,2) = + 175 кДж.

Таким образом, термическое разложение NH₄Cl является эндотермической реакцией. Термохимическое уравнение имеет вид

NH₄Cl(к) → NH₃(г) + HCl(г) - 175 кДж.

Пример 2. Тепловой эффект реакции С(т) + ½О₂(г) = СО(г) при постоянном объеме и температуре 20º С равен 108,9 кДж. Определить тепловой эффект реакции при постоянном давлении.

Решение. Соотношение между тепловым эффектом при
V = const (Q_V =∆U) и тепловым эффектом при р = const (Q_р =∆H) выражается уравнением ∆H = ∆U + р∆V. Определяем изменение числа молей газов в ходе реакции:

∆n = 1 - ½ = ½ (моль).

Учитывая значение Т = 293 К, R = 8,314 Дж/моль·К, а также единицы измерения величин, получаем для теплового эффекта реакции при р = const

∆H = ∆U + ∆n R T = - 108,9+1/2·8,314 /10³·293 = - 107,68 кДж.

Пример 3. Возможен ли процесс получения металлического железа из оксида Fe₂O₃ действием водорода при стандартных условиях Fe₂O₃(к) + 3H₂(г) = 2Fe(к) + 3H₂O(ж)? Как скажется повышение температуры на вероятности протекания этой реакции?

Решение. Для ответа на первый вопрос задачи необходимо
рассчитать изменение свободной энергии Гиббса ∆G⁰₂₉₈ для
рассматриваемой реакции, используя уравнение ∆G_{T(реакции)} =
= ∆H_{T (реакции)} − T∆S_{Т(реакции)}. Значения ∆H⁰₂₉₈ и ∆S⁰₂₉₈ для всех веществ, участвующих в реакции, приводятся в задании или берутся из таблиц термодинамических величин.

По следствию из закона Гесса ∆H⁰_{298(реакции)} =
= ∑(n'∆_fH⁰₂₉₈)_прод − ∑(n''∆_fH⁰₂₉₈)_исх,найдем

∆H⁰_{298(реакции)} = 3∆H⁰₂₉₈ (H₂O)(ж) – ∆H⁰₂₉₈(Fe₂O₃)(к) = 3 (-285,8) – (-822,0)=

= - 857,4 + 822,0 = - 35,4 кДж.

Значение ∆H⁰₂₉₈ (H₂)(г) = 0 и ∆H⁰₂₉₈ (Fe)(к) = 0.

Согласно

∆S⁰_{298(реакции)}= ∑(n'S⁰₂₉₈)_прод − ∑(n''S⁰₂₉₈)_исх,

найдем

∆S⁰_{298(реакц)} =[3S⁰₂₉₈(H₂O)(ж) + 2S⁰₂₉₈(Fe)(к)] - [S⁰₂₉₈ (Fe₂O₃)(к) +

+ 3S⁰₂₉₈(H₂)(г)] = (3·70,1 + 2·2,27) - (87,0 + 3·130,5) = - 213,8 Дж/К.

По найденным данным вычисляем

∆G⁰₂₉₈ = ∆H⁰₂₉₈ − T∆S⁰₂₉₈ = - 35,4 + 213,8·10^-3·298 = 28,34 кДж.

Положительное значение ∆G указывает на невозможность восстановления Fe₂O₃ водородом при стандартных условиях.

Ответ на второй вопрос задачи определяется знаком ∆S. Рас-
чет показал, что ∆S⁰_{298реакции} < 0, следовательно, в уравнении ∆G = ∆H − T∆S величина −T∆S > 0. Повышение температуры приводит к увеличению значения ∆G, а значит, не будет способствовать протеканию реакции в прямом направлении.

Пример 4. Определить стандартный тепловой эффект реакции, если известны теплоты образования веществ.

1. Реакция образования сульфата алюминия из оксида алюминия и триоксида серы:

Al₂O_{3 (кр)} + 3SO_{3 (газ)} = Al₂(SO₄)_{3 (кр)}.

Вещество	Al2O3 (кр)	SO3 (газ)	Al2(SO4)3 (кр)
DfН0298, кДж/моль	–1676,1	–395,9	–3442,8

Решение. Тепловой эффект реакции определяем по первому следствию из закона Гесса. В соответствии с уравнением реакции

D_rН⁰₂₉₈=(1×D_fН⁰_Al2(SO4)3)–(1×D_fН⁰_Al2O3 + 3×D_fН⁰_SO3 ) =

=1 (–3442,8) – [1 (–1676,1) + 3(–395,9)] = –579 [кДж].

2. Реакция взаимодействия метана и диоксида углерода с образованием оксида углерода и водорода:

CH_{4 (газ)} + CO_{2 (газ)} = 2 CO _(газ) + 2H_{2 (газ)}.

Вещество	CH4 (газ)	CO2 (газ)	CO (газ)	H2 (газ)
DfН0298, кДж/моль	–74,85	–393,51	–110,5

Решение. Тепловой эффект реакции определяем по следствию из закона Гесса. В соответствии с уравнением реакции

D_rН⁰₂₉₈=(2×D_fН⁰_CO + 2×D_fН⁰_H2)–(1 D_fН⁰_CH4 + 1 D_fН⁰_CO2) =

=[2 (–110,5) + 2×0] – [1 (–74,85) + 1 (–393,51)] = 247,36 [кДж].

Пример 5. Определить стандартный тепловой эффект реакции, если известны стандартные теплоты сгорания веществ. Реакция взаимодействия уксусной кислоты и этилового спирта с образованием сложного эфира – этилацетата:

CH₃COOH_(ж) + C₂H₅OH_(ж) = CH₃COOC₂H_5(ж) + H₂О_(ж).

Вещество	CH3COOH(ж)	C2H5OH(ж)	CH3COOC2H5(ж)	H2О(ж)
DcН0298, кДж/моль	–873,79	–1366,91	–2254,21

Решение. Тепловой эффект реакции определяем по следствию из закона Гесса. В соответствии с уравнением реакции

D_rН⁰₂₉₈ =(1 D_cН⁰_ук + 1 D_cН⁰_эс)–(1 D_cН⁰_эа + 1 D_cН⁰_H2O) =

= [1 (–873,79) +1 (–1366,91)] – [1 (–2254,21)+ 1×0] = 13,51[кДж].

Пример 6. Определить изменение энтропии в стандартных условиях при протекании реакции:

CH_{4 (газ)} + CO_{2 (газ)} = 2CO _(газ) + 2H_{2 (газ)}.

Вещество	CH4 (газ)	CO2 (газ)	CO (газ)	2H2 (газ)
S0298, Дж/моль×К	186,27	213,66	197,55	130,52

Решение. D_r S⁰₂₉₈=(ån_i S⁰_298i)_{продукты}–(ån_i iS⁰_298i)_{исх. вещества},

D_r S⁰₂₉₈ = (2×197,55 + 2×130,52) – (1×186,27 + 1×213,66) = 256,21 [Дж/K].

Пример 7.Определить направление самопроизвольного протекания реакции взаимодействия оксида кальция и воды с образованием дигидроксида кальция в стандартных условиях:

CaO_(кр) + H₂O_(ж) = Ca(OH)_2(кр).

Вещество	CaO(кр)	H2O(ж)	Ca(OH)2(кр)
DfG0298, кДж/моль	–603,46	–237,23	–897,52
DfH0298, кДж/моль	–635,09	–285,83	–985,12
S0298, Дж/моль×К	38,07	69,95	83,39

Решение. Направление самопроизвольного протекания реакции определяется по изменению энергии Гиббса (D_rG⁰ < 0).

1. Зная величины D_fG⁰ для реагентов, можно непосредственно вычислить изменение энергии Гиббса в ходе реакции:

D_r G⁰₂₉₈ = (å n_i D_fG⁰_i)_прод – (å n_i D_fG⁰_i)_{исх. вещества},

D_r G⁰₂₉₈ = (1(–897,52)) – [1(–603,46) + 1(–237,23)] = –56,83 (кДж).

Следовательно, данная реакция в стандартных условиях может самопроизвольно протекать в прямом направлении.

2. Изменение энергии Гиббса можно также вычислить по тепловому эффекту и энтропии реакции:

D_r G⁰₂₉₈ = D_r Н⁰₂₉₈ –298 D_r S ⁰₂₉₈,

D_r Н⁰₂₉₈ = (å n_i D_fН⁰_298i)_прод – (å n_i D_fН⁰_298i)_{исх. вещества},

D_r S⁰₂₉₈ = (ån_i S⁰_298i)_прод – (ån_i S⁰_298i) _{исх. вещества},

D_r Н⁰₂₉₈ = (1(–985,12)) – (1(–635,09) + 1(–285,83)) = –64,2 (кДж),

D_r S⁰₂₉₈ = (1×83,39) – (1×38,07 + 1×69,95) = –24,63 (Дж/K),

D_r G⁰₂₉₈ = –64,2 – 298(–24,63×10^-3) = –56,86 (кДж).

Результаты первого и второго расчетов, естественно, совпадают (с учетом погрешности).

Пример 8. Определить возможность самопроизвольного окисления ртути кислородом в стандартных условиях (прямая реакция) и температуру, при которой возможен самопроизвольный распад окиси ртути на ртуть и кислород (обратная реакция):

Hg(ж) + ½ O₂(газ) = HgO(кр).

Вещество	Hg(ж)	O2(газ)	HgO(кр)
DfH0298, кДж/моль			–90,88
S0298, Дж/моль×К	75,90	205,04	70,29

Решение. Изменение энергии Гиббса в ходе реакции вычисляют по тепловому эффекту и энтропии реакции при Т=298 К:

D_r G⁰(Т) » D_r Н⁰₂₉₈ – Т D_r S⁰₂₉₈,

D_r Н⁰₂₉₈ = (å n_i D_fН⁰_298i)_прод – (å n_i D_fН⁰_298i)_{исх. вещества},

D_r S⁰₂₉₈ = (ån_i S⁰_298i)_прод – (ån_i S⁰_298i) _{исх. вещества},

D_r Н⁰₂₉₈ = 1(–90,88) – (1×0 +½×0) = –90,88 кДж/моль,

D_r S⁰₂₉₈ = 1×70,29 – (1×75,90 +½×205,04) = –108,13 Дж/моль×K,

D_r G⁰₂₉₈ = –90,88 – 298(–108,13×10^-3) = –58,65 кДж/моль.

Поскольку D_rG⁰₂₉₈ < 0, то окисление ртути в стандартных условиях возможно.

Самопроизвольное разложение окиси ртути на кислород и ртуть возможно, если для обратной реакции 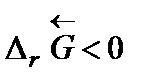. Поскольку 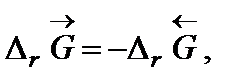то обратная реакция по отношению к окислению возможна, если D_rG⁰(Т) » D_r Н⁰ – Т D_r S ⁰ > 0, что выполняется при температуре выше 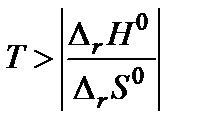= 840,47 К.

Библиографический список

1. Коровин, Н.В. Общая химия. М.: Высшая школа, 2000.

2. Стромберг, А.Г., Семченко Д.П. Физическая химия / Под ред. А.Г. Стромберга. М.: Высшая школа, 2001.

3. Фримантл, М. Химия в действии: В 2 ч. / Пер. с англ. М.: Мир, 1991.

4. Киселев, А.П., Крашенинников А.А. Основы общей химии: учебное
пособие / Балт. гос. техн. ун-т. СПб., 2012.

5. Кудряшов, И.В., Каретников Г.С. Сборник примеров и задач по физической химии: учебное пособие. М.: Высшая школа, 1991.

О Г Л А В Л Е Н И Е

1. ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ.. 3

1.1. Энергия. 3

2. ПЕРВЫЙ ЗАКОН (НАЧАЛО) ТЕРМОДИНАМИКИ.. 6

2.1. Термодинамическая функция энтальпия. 7

2.2. Тепловой эффект реакции. 8

2.3. Закон Гесса. Термохимические расчеты.. 9

2.4. Зависимость теплового эффекта реакции от температуры.. 10

3. ВТОРОЙ ЗАКОН (НАЧАЛО) ТЕРМОДИНАМИКИ.. 11

3.1. Понятие энтропии. 12

3.2. Изменение энтропии в некоторых процессах. 14

3.3. Направленность самопроизвольных процессов. Свободная энергия Гиббса 16

4. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ.. 19

Библиографический список. 23

Барунин Анатолий Анатольевич, Маслобоев Дмитрий Степанович

Термодинамические расчеты

Редактор Г.М. Звягина

Корректор Л.А. Петрова

Подписано в печать 19.02.2016. Формат 60х84/16. Бумага документная.

Печать трафаретная. Усл. печ. л. 1,5. Тираж 200 экз. Заказ № 45.

Балтийский государственный технический университет

Типография БГТУ

190005, С.-Петербург, 1-я Красноармейская ул., д.1