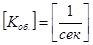Материальный баланс процессов массообмена

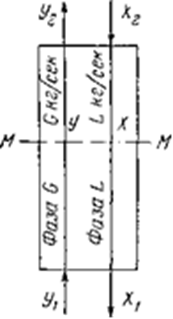
Рассмотрим схему движения потоков в противоточном аппарате для массообмена (рис. 1-2). В аппарат поступают фазы (например, газ) и (например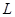, жидкость). Пусть расход носителя в фазе составляет кг/сек, а в фазе 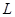равен 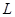кг/сек. Содержание распределяемого компонента, выраженное в виде относительных весовых составов, в фазе обозначим через , в фазе 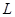— через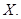

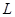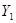Предположим, что распределяемый компонент переходит из фазы в фазу (например, абсорбируется из газовой смеси жидкостью), причем содержание этого компонента в фазе уменьшается от (на входе в аппарат) до 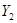(на выходе из аппарата). Соответственно содержание этого же компонента в фазе 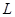увеличивается от (при входе в аппарат) до (на выходе из аппарата).

Носители не участвуют в процессе массообмена; следовательно, их количества и 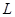не изменяются по длине аппарата. Тогда количество компонента, перешедшего из фазы , составит:

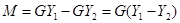кг/сек

и количество компонента, перешедшего в фазу :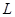

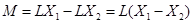кг/сек

Оба эти количества равны, поэтому можно написать уравнение материального баланса в следующем виде:

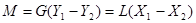(1-14)

Отсюда находим соотношения между ко­личествами носителя в обеих фазах:

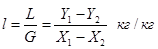(1-15)

Рассмотрим произвольное сечение аппара­та ММ, в котором составы фаз будут и 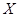и напишем уравнение материального баланса для части аппарата, расположенной выше этого сечения:

откуда

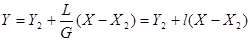(1-16)

Уравнение (1-16), называемое уравнением рабочей линии, выражает зависимость между неравновесными составами фаз ( , 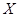) в любом сечении аппарата.

Как видно из этого уравнения, на диаграмме — 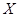рабочая линия представляет собой прямую с наклоном к оси абсцисс под углом, тангенс которого равен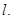

Подставив в уравнение (1-16) значение 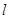из уравнения (1-15), получим после простейших преобразований:

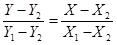
Это выражение является уравнением прямой (см. рис. 1-1), проходящей через точку А с координатами , 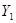и через точку В с координатами , . 

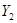На рис. 1-1 рабочая линия расположена выше линии равновесия, т. е. рабочие концентрации распределяемого компонента в фазе выше равновесных концентраций и компонент переходит из фазы в фазу 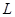. Если компонент переходит из фазы 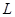в фазу , то рабочие концентрации в фазе ниже равновесных; в этом случае рабочая линия расположена ниже линии равновесия.

Пример 1-5. Аммиак поглощается водой из газа (воздух) с начальным содержанием NH₃ 5 объемн. %, конечное содержание NH₃ в газе 0,27 объемн. %. Количество поступающего газа 10 000 м³/ч (при нормальных условиях). Общее давление газа 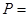760 мм рт ст. Содержание NH₃ в поступающей на абсорбцию воде 0,2 вес.%, удельный расход поглотителя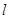 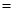1,18 кг/кг Определить количество поглощенного аммиака, конечную концентрацию его в воде и построить рабочую линию данного процесса абсорбции.

Р е ш е н и е Количество инертного газа (воздуха) составляет (при нормальных условиях):

10 000 (1 — 0,05) = 9 500 м³/ч

или

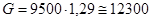кг/ч

где 1,29 — плотность воздуха при нормальных условиях, кг/м³.

Относительные весовые составы газовой фазы определяем по формуле (1-12), заменяя в ней величины давления на пропорциональные им объемные содержания

на входе

на выходе

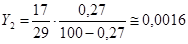
Количество поглощенного аммиака составляет:

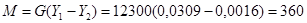кг/ч

Определяем расход воды:

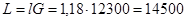кг/ч

Концентрация аммиака в поступающей на абсорбцию воде составит (в относительных весовых единицах):

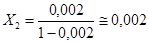
Конечную концентрацию аммиака в поглощающей воде определяем по уравнению (1-15):

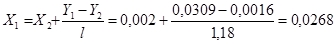
Уравнение рабочей линии по формуле (1-16) имеет следующий вид:

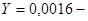
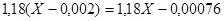
Для построения рабочей линии на — 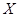-диаграмме (см рис. 1-5) проводим прямую через точку А (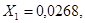 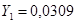) и точку В ( ).

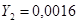Уравнение массопередачи

При отклонении от состояния равновесия происходит переход вещества из фазы, в которой его содержание выше равновесного, в фазу, где содержание этого вещества ниже равновесного.

Скорость перехода вещества пропорциональна степени отклонения от равновесия, которую можно выразить как разность концентраций — рабочей концентрации вещества в одной из фаз и равновесной концентрации в ней данного вещества. Эта разность концентраций является движущей силой процесса массопередачи. Кроме того, скорость перехода вещества пропорциональна поверхности соприкосновения фаз.

Скорость перехода вещества можно определить как количество вещества, переходящего в единицу времени из одной фазы в другую. Тогда уравнение массопередачи можно написать в следующем виде:

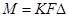(1-17)

где 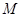— количество вещества, перешедшего из одной фазы в другою, кг/сек;

— коэффициент пропорциональности, называемый коэффициентом массопередачи;

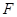— поверхность соприкосновения фаз, м²;

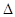— движущая сила процесса массопередачи.

Уравнение (1-17) аналогично уравнению теплопередачи: температурному напору соответствует движущая сила процесса массопередачи, количеству тепла — количество вещества, переходящего из одной фазы в другую, коэффициенту теплопередачи — коэффициент массопередачи.

Движущая сила 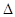может быть выражена в любых единицах, применяемых для выражения составов фаз. При этом размерность коэффициента массопередачи

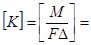
определяется единицами, принятыми для выражения движущей силы.

Из этого уравнения следует, что коэффициент массопередачи выражает количество вещества, переходящего из одной фазы в другую за единицу времени через единицу поверхности соприкосновения при движущей силе, равной единице.

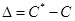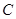Если движущая сила выражается в виде разности объемных концентраций (кг/м³), то , где — фактическая концентрация компонента в одной из фаз, — равновесная концентрация компонента в той же фазе. Тогда уравнение (1-17) примет вид

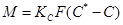(1-18)

причем размерность коэффициента массопередачи

Если рабочая концентрация 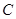в данной фазе выше равновесной концентрации , вещество будет переходить из этой фазы в другую фазу, а движущая сила будет равна разности фактической и равновесной концентрации .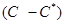

Движущую силу процессов массообмена, протекающих в газовой фазе (например, при абсорбции), часто выражают через разность парциальных давлений 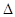= 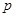— 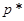(в н/м²), где 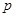— фактическое парциальное давление компонента в газе, 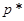— парциальное давление компонента в газе при равновесии его с жидкостью. Размерность коэффициента массопередачи 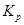, выраженного через разность парциальных давлений:

Связь между коэффициентами массопередач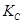и и 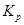на основании формулы (1-10) выражается соотношением:

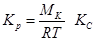сек/м (1-19)

Если движущая сила выражена через разность долей, коэффициент массопередачи будет равен:

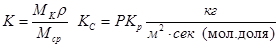(1-20)

Если же движущая сила выражена в виде разности относи-тельных весовых составов (кг/кг), то при небольших концентрациях компонента коэффициент массопередачи составит: 

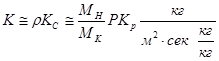
В этих формулах:

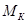и 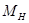— молекулярные массы компонента и носителя;

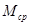— средняя молекулярная масса фазы;

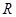— газовая постоянная (8314 дж/кмоль ∙ град);

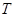— абсолютная температура, °К;

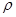— плотность фазы, кг/м³:

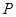—общее давление, н/м².

При практических расчетах за единицу времени часто принимают ч, а за единицу разности парциальных давлений — ат или мм рт. ст. Тогда размерность коэффициента массопередачи 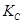будет м/ч, а 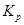— кг/м² ∙ ч ∙ ат или кг/м² ∙ ч ∙ мм рт. ст. Для пересчета коэффициентов массопередачи в нужные значения надо соответствующую величину коэффициента умножить на следующие переводные множители:

м/сек X 3600 = м/ч

сек/м X 3,53 ∙ 108 = кг/м² ∙ ч ∙ ат

сек/м X 4,8 ∙ 105 = кг/м² ∙ ч ∙ мм рт. ст.

кг/м² ∙ ч ∙ мм рт. ст. X 735 = кг/м² ∙ ч ∙ ат

Иногда коэффициент массопередачи относят к единице рабочего объема аппарата (объемный коэффициент массопередачи). В этом случае коэффициент массопередачи определяется соотношением

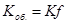(1-22)

где — поверхность соприкосновения фаз, отнесенная к единице рабочего объема аппарата, м²/м³.

Размерность объемного коэффициента массопередачи при движущей силе 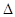, выраженной в кг/м³: