Работа электростатических сил. Потенциал. Связь напряженности и потенциала электростатического поля

Список основных формул

Потенциал φ –энергетическая характеристика поля, равная отношению потенциальной энергии 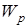пробного заряда 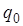, помещенного в данную точку поля, к величине этого заряда

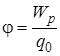(8.1)

Потенциал φ поля, созданного точечным зарядом q

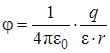, (8.2)

где, r – расстояние от точечного заряда до заданной точки поля.

принцип суперпозиции для потенциала:

- если электростатическое поле создается несколькими зарядами, то потенциал j результирующего поля равен алгебраической сумме потенциалов полей, созданных каждым зарядом по отдельности

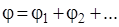(8.3)

- если поле создано макроскопическим заряженным телом, то

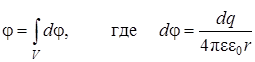, (8.4)

где 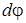– потенциал поля созданного точечным зарядом dq, сосредоточенном в бесконечно малом объеме тела dV.

Потенциальная энергия W_p взаимодействия двух точечных зарядов

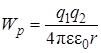, (8.5)

где q₁ и q₂–величины взаимодействующих электрических зарядов; r – расстояние между ними.

Потенциальная энергия W_p системы точечных зарядов ( )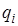

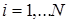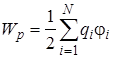, (8.6)

где 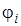–потенциал поля, созданного всеми зарядами, кроме i-го заряда, в месте расположения i-го заряда.

Работа сил электростатического поля по перемещению точного заряда из точки 1 в точку 2может быть вычислена по формулам:

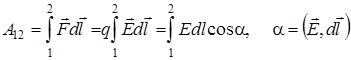; (8.7)

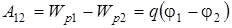, (8.8)

где 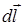- вектор элементарного перемещения, j₁ и j₂ – потенциалы электростатического поля в точках 1 и 2 соответственно.

Связь между напряженностью и потенциалом электростатического поля имеет вид:

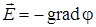(8.9)

В случае радиально-симметричного поля формула (8.9) примет вид:

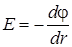, (8.10)

где r – координата точки поля по радиальной оси.

Для однородного поля формула (8.10) принимает вид

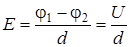, (8.11)

где 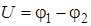– напряжение между точками 1 и 2, а d – расстояние между эквипотенциальными поверхностями с потенциалами j₁ и j₂.

Из выражений (8.7), (8.8) можно получить интегральную формулу связи 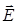иφ, в которую входят две точки поля:

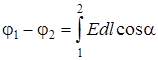. (8.12)

Электроемкость. Энергия электрического поля

Список основных формул

Электроемкость уединенного проводника – скалярная физическая величина, характеризующая способность проводника накапливать электрический заряд и численно равная

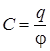, (9.1)

где q – заряд проводника, j – его потенциал.

Электроемкость уединенной металлической сферы

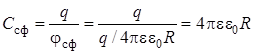, (9.2)

где R – радиус сферы, e – диэлектрическая проницаемость среды, в которой находится проводник.

Электроемкость конденсатора характеризует способность конденсатора накапливать электрический заряд и численно равна

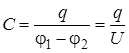, (9.3)

где q – заряд конденсатора, 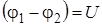– разность потенциалов (напряжение) между его обкладками.

Электроемкость плоского конденсатора

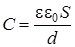, (9.4)

где S – площадь одной пластины конденсатора; d – расстояние, а 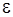– относительная диэлектрическая проницаемость среды между обкладками конденсатора.

Емкость сферического конденсатора

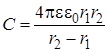, (9.5)

где 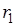и 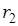– радиусы внутренней и внешней обкладок соответственно, ε – диэлектрическая проницаемость среды, заполняющей пространство между обкладками.

Емкость цилиндрического конденсатора

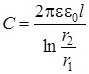, (9.6)

где 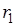и 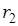– радиусы внутренней и внешней обкладок соответственно, l – высота одной обкладки, ε – диэлектрическая проницаемость среды, между обкладками конденсатора.

Энергия уединенного заряженного проводника

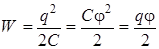, (9.7)

Энергия заряженного конденсатора

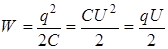. (9.8)

Объемная плотность энергии электростатического поля

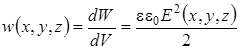, (9.9)

где dW – энергия электростатического поля, заключенная в элементарном объеме dV вблизи точки пространства с координатами (x,y,z), E – напряженность электрического поля вблизи точки с координатами (x,y,z).

Энергия W электрическогополя в любом конечном объеме V пространства может быть рассчитана через объемную плотность энергии w по формуле:

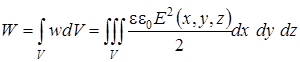. (9.10)

Расчет магнитных полей

Список основных формул.

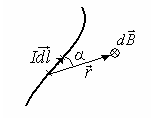
Закон Био-Савара-Лапласа

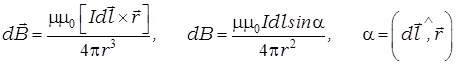. (11.1)

где 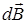– индукция магнитного поля, создаваемого элементом тока 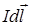; 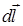– вектор, равный по модулю длине 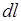проводника и совпадающий по направлению с током, 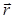– радиус-вектор, проведенный от элемента тока к рассматриваемой точке пространства, 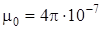Гн/м – магнитная постоянная, m – магнитная проницаемость среды (для вакуума и воздуха m = 1).

Принцип суперпозиции для магнитных полей:

если поле создано проводником с током произвольной конфигурации, то

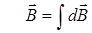, (11.2)

в случае если магнитное поле создается несколькими проводниками с токами, то

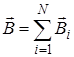. (11.3)

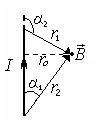Модуль вектора магнитной индукции, создаваемого прямолинейным отрезком проводника конечной длины с током

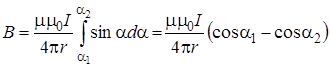, (11.4)

где r – кратчайшее расстояние от рассматриваемой точки до проводника или его продолжения; a₁, a₂ – углы между первым и последним элементами тока и радиус-векторами, проведенных от них в рассматриваемую точку.

Для поля бесконечно длинного прямолинейного проводником с током имеем

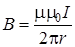, (11.5)

где формула (11.5) является частным случаем (11.4) при α₁→0⁰, α₂→180⁰

Модуль вектора магнитной индукции на оси (В) и в центре (В₀) кольцевого тока

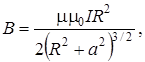(11.6)

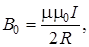(11.7)

где R – радиус кольца; а – расстояние от центра кольцевого тока до рассматриваемой точки, находящейся на оси кольца.

Теорема о циркуляции вектора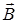

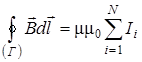(11.8)

Индукция магнитного поля, внутри бесконечно длинного соленоида (длина соленоида значительно больше диаметра витков)

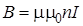, (11.9)

где 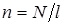– число витков на единицу длины соленоида.

Индукция магнитного поля внутри тороида

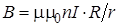(11.10)

где 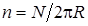– число витков, приходящихся на единицу длины тороида, 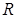– радиус окружности, проходящей через центры витков тороида.