Энтропия. Термодинамические циклы

Список основных формул.

Коэффициент полезного действия теплового двигателя (КПД)

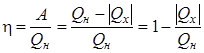, (6.1)

где Q_н и Q_х – количества теплоты, полученные от нагревателя и отданные холодильнику, соответсвенно.

Максимальный КПД идеального теплового двигателя (КПД цикла Карно)

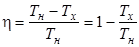, (6.2)

где Т_н и Т_х – температуры нагревателя и холодильника.

Изменение энтропии при обратимом процессе в термодинамической системе

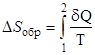, (6.3)

где 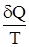– приведенная теплота.

Изменение энтропии при необратимом процессе

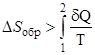. (6.4)

Второе начало термодинамики (по Клаузиусу): энтропия замкнутой системы стремится к максимуму:

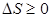. (6.5)

Если в термодинамической системе происходит несколько процессов, то полное изменение энтропии в конце процессов равно

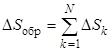, (6.6)

где N – количество происходящих в термодинамической системе процессов, 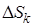– изменение энтропии в ходе k-го процесса.

Изменение энтропии в ходе изотермического процесса:

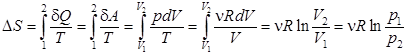. (6.7)

Изменение энтропии в ходе изохорического процесса:

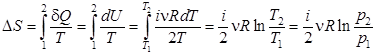. (6.8)

Изменение энтропии в ходе изохорического процесса:

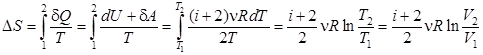(6.9)

Изменение энтропии при адиабатном процессе:

Так как теплота не подводится ( 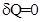), то во всех равновесных адиабатных процессах

DS=0, S=const. (6.10)

Список основных формул

Свойство дискретности электрического заряда: заряд q любого тела кратен элементарному заряду

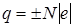, (9.1)

где 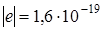Кл – элементарный заряд (минимальный заряд, существующий в природе, им обладают электроны и протоны), N – число избыточных электронов или протонов на теле

Закон сохранения электрического заряда: алгебраическая сумма электрических зарядов частиц замкнутой системы остается постоянной

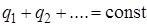. (9.2)

Закон Кулона позволяет вычислить силу электростатического взаимодействия между двумя точечными зарядами:

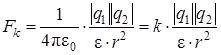, (9.3)

где q₁ и q₂–величины взаимодействующих электрических зарядов; r – расстояние между ними; ε – диэлектрическая проницаемость среды, в которой находятся заряды (ε = 1 для вакуума, и с достаточной степенью точности можно принять ε = 1 для воздуха), 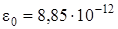Ф/м – электрическая постоянная, 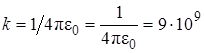Н×м²/Кл².

Напряженность электростатического поля 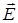– силовая характеристика поля, равная отношению кулоновской 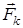силы, действующей на пробный положительный заряд q₀, помещенный в данную точку поля, к величине этого заряда

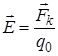. (9.4)

Напряженность E поля, созданного точечным зарядом q

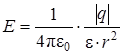(9.5)

Принцип суперпозиции:

- если электростатическое поле создается несколькими зарядами, то вектор напряженности результирующего поля равен векторной сумме напряженностей полей, созданных каждым зарядом по отдельности ( )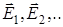

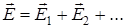(9.6)

- если поле создано макроскопическим заряженным телом, то

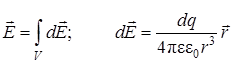, (9.7)

где 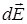– напряженность поля созданного точечным зарядом dq, содержащимся в бесконечно малом объеме тела dV.

Напряженность электрического поля в точке, находящейся на оси заряженного кольца вычисляется по формуле

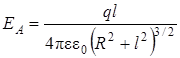, (9.8)

где q – заряд кольца, R – радиус кольца, l – расстояние от центра кольца до точки, лежащей на его оси.

Теорема Гаусса: поток вектора 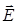через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов 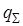, охватываемых этой поверхностью, и деленной на εε₀

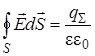, (9.9)

где 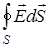– поток вектора напряженности через произвольную замкнутую поверхность S. Если поле создано системой зарядов, то под суммой зарядов следует понимать алгебраическую сумму всех зарядов, охватываемых поверхностью :

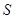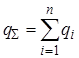. (9.10)

В случае, если заряды распределены непрерывно, то суммарный заряд вычисляется по одной из формул:

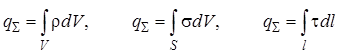, (9.11)

где ρ, σ, τ – объемная, поверхностная и линейная плотности заряда, соответственно; V, S, l –соответственно, объем, поверхность, линия, по которым распределены заряды, охватываемые поверхностью интегрирования.

С помощью теоремы Гаусса можно вычислять напряженности полей созданных различными заряженными телами.

Напряженность поля, созданного бесконечно протяженной заряженной плоскостью с поверхностной плотностью заряда σ:

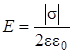, (9.12)

Поле равномерно заряженной (с линейной плотностью заряда τ) бесконечно длинной нити:

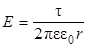. (9.13)

Поле равномерно заряженной по поверхности сферырадиусом R:

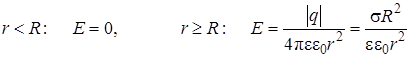, (9.14)

где r – расстояние от центра сферы, до рассматриваемой точки, 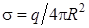– поверхностная плотность заряда на сфере.