Кинематика и Динамика Вращательного движения

Кинематика и Динамика Вращательного движения

Список основных формул

Угловая скорость ( 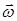) – векторная физическая величина, характеризующая быстроту вращения (поворота), численно равная первой производной вектора углового перемещения по времени:

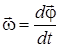(3.1)

Углового ускорения ( 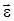) – векторная физическая величина, характеризующая быстроту изменения вектора угловой скорости, численно равная первой производной вектора угловой скорости по времени:

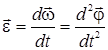(3.2)

Формулы связи кинематических величин поступательного и вращательного движений

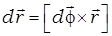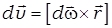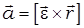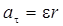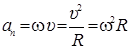; , ; ; (3.3)

Формулы расчета 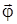и для вращательного движения м.т.

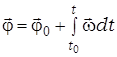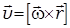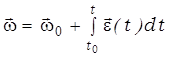, , (3.4)

Момент инерции м.т. и а.т.т. относительно оси вращения – скалярная физическая величина, являющаяся мерой инертности м.т. и а.т.т. при их вращательном движении, численно равная:

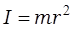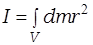и (3.5)

Момент силы относительно оси вращения – векторная физическая величина, равная векторному произведению вектора силы 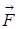и вектора 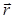, перпендикулярного к оси вращения, и, соединяющего точку приложения силы с осью вращения:

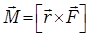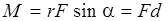, (3.6)

где 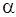– угол между векторам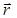и и 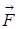, 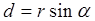– плечо силы (кратчайшее расстояние между осью вращения и линией действия силы);

Основной закон динамики вращательного движения

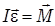(3.7)

Теорема Штейнера:

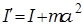(3.8)

где I, I' - моменты инерции тела массы m относительно оси, проходящий через центр масс тела (I) и оси параллельной ей (I'), отстоящей от нее на расстоянии .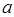

Моменты инерций некоторых тел относительно осей симметрии:

обруч (или тонкостенный цилиндр) массы m и радиуса r:

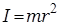(3.9)

сплошной однородный диск (или цилиндр) массы m, радиуса R и высоты h:

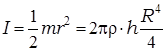(3.10)

где 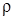– плотность материала диска;

однородный шар массы m и радиуса r

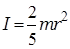(3.11)

тонкий однородный стержень массы m и длины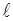

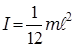(3.12)

МОМЕНТ импульса. Законы сохранения МОМЕНТА импульса. Работа и энергия при Вращательнм движении

Список основных формул

момент импульса м.т. ( ) – векторная физическая величина, определяемая векторным произведением вектора 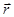, соединяющего м.т. с осью вращения и перпендикулярного к этой оси, и вектора импульса тела :

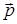, (4.1)

где 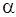– угол между векторам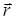и и 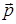, 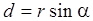– прицельное расстояние (кратчайшее расстояние между осью вращения и линией движения тела).

момент импульса а.т.т. ( 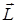) относительно оси вращения – векторная физическая величина, равная векторной сумме моментов импульсов всех точек этого тела.

Основной закон динамики вращательного движения

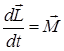(4.2)

Закон сохранения момента импульса

Суммарный момент импульса замкнутой системы тел остается постоянным относительно любой оси вращения:

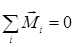Þ или 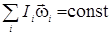. (4.3)

В данном случае под замкнутой системой тел подразумевается система тел, на которые не действуют моменты внешние силы ( 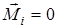) или их сумма равна нулю ( ).

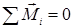Работа сил при вращательном движении (теорема о кинетической энергии для вращающегося тела)

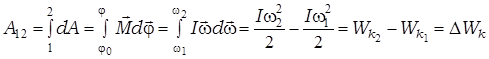(4.4)

Кинетическая энергия тела при вращении тела вокруг одной оси

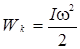(4.5)

в случае катящегося тела

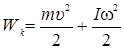(4.6)

Список основных формул.

Количество вещества (число молей газа)

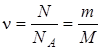, (5.1)

где N – число молекул; N_A = 6,02^.10²³ моль^-1– постоянная Авогадро, m – масса газа, M – молярная масса газа.

Плотность газа

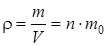, (5.2)

где n – концентрация газа (число молекул в единице объема), m₀ – масса молекулы газа.

Уравнение Клапейрона–Менделеева (уравнение состояния идеального газа)

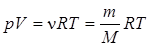,(5.3)

где V – объем газа; p – давление газа; Т – абсолютная температура; R = 8,31 Дж/(моль×К) – универсальная газовая постоянная.

Закон Бойля – Мариотта (изотермический процесс, Т = const)

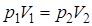. (5.4)

Закон Гей-Люссака (изобарический процесс, p = const)

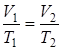. (5.5)

Закон Шарля (изохорический процесс, V = const.)

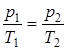. (5.6)

Закон Дальтона для давления смеси газов

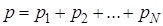(5.7)

где p₁, p₂, … , p_N – парциальные давления газов, находящихся в смеси (парциальное давление – такое давление, которое газ при данной температуре оказывал бы на стенки сосуда, если бы он один заполнял весь объем).

Основное уравнение молекулярно – кинетической теории (МКТ)

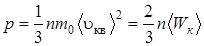, (5.8)

где 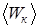– средняя кинетическая энергия теплового движения молекулы газа; k= 1,38×10-23Дж/К – постоянная Больцмана; 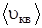– среднеквадратическая скорость молекул.

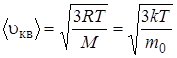. (5.9)

Связь между давлением идеального газа и температурой

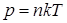. (5.10)

Средняя кинетическая энергия одной молекулы

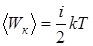, (5.11)

где i – число степеней свободы молекулы (i = 3 – для одноатомного газа; i= 5 – для двухатомного газа, i = 6 – для многоатомного газа)

Функция распределения молекул по модулю скорости (функции распределения Максвелла)

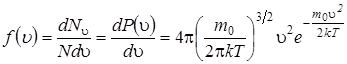(5.12)

Наиболее вероятная скорость молекул идеального газа вычисляется по формуле:

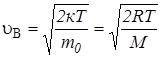, (5.13)

Средняя скорость теплового движения молекул

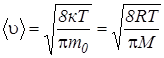. (5.14)

Барометрическая формула – описывает распределение давления по высоте в атмосфере Земли и других планет:

, (5.15)

где р – давление газа на высоте h; р₀ – давление газа на высоте h = 0; g – ускорение свободного падения.

Зависимость концентрации молекул газа от высоты

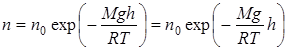(5.16)

где n – концентрация молекул на высоте h; n₀ – концентрация молекул на высоте h = 0

Молярные теплоемкости при постоянном объеме c_v и постоянном давлении c_p соответственно равны

. (5.17)

Связь между молярной (c) и удельной (с_уд) теплоемкостями газа

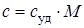. (5.18)

где М – молярная масса газа.

Внутренняя энергия идеального газа – суммарная кинетическая энергия молекул газа

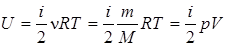. (5.19)

Работа равновесного расширения газа при изменении объема от V₁ до V₂

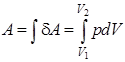. (5.20)

Первое начало термодинамики: количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на работу, совершаемую системой над внешними телами

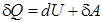, (5.21)

где δQ и δA означают элементарное количество теплоты и элементарную работу в ходе процесса, при котором внутренняя энергия системы изменилась на бесконечно малую величину dU.

Первое начало термодинамики для процесса, при котором изменение параметров системы является конечным можно записать в виде

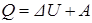, (5.22)

где Q –конечное количество тепла, сообщенное термодинамической системе (газу) или отданное ею; DU – конечное изменение внутренней энергии системы; А –полная работа, совершенные термодинамической системой.

Применение первого начала термодинамики к различным процессам::

1. Изотермический процесс: Т = const, DU = 0,

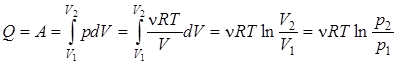. (5.23)

2. Изохорический процесс: V = const, 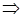A = 0,

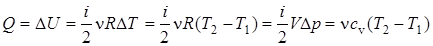. (5.24)

3. Изобарический процесс: p = const.

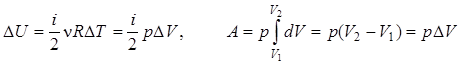
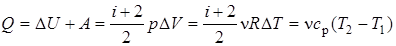. (5.25)

4. Адиабатический процесс: Q = 0,

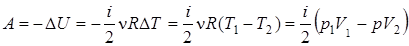. (5.26)

Уравнение Пуассона (уравнение газового адиабатного процесса)

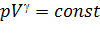, (5.27)

где 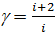– показатель адиабаты (коэффициент Пуассона)

5. Круговой процесс (цикл): DU_кр = U₁ – U₁ = 0,

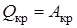. (5.28)

Список основных формул.

Коэффициент полезного действия теплового двигателя (КПД)

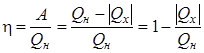, (6.1)

где Q_н и Q_х – количества теплоты, полученные от нагревателя и отданные холодильнику, соответсвенно.

Максимальный КПД идеального теплового двигателя (КПД цикла Карно)

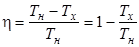, (6.2)

где Т_н и Т_х – температуры нагревателя и холодильника.

Изменение энтропии при обратимом процессе в термодинамической системе

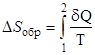, (6.3)

где 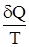– приведенная теплота.

Изменение энтропии при необратимом процессе

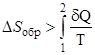. (6.4)

Второе начало термодинамики (по Клаузиусу): энтропия замкнутой системы стремится к максимуму:

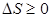. (6.5)

Если в термодинамической системе происходит несколько процессов, то полное изменение энтропии в конце процессов равно

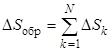, (6.6)

где N – количество происходящих в термодинамической системе процессов, 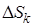– изменение энтропии в ходе k-го процесса.

Изменение энтропии в ходе изотермического процесса:

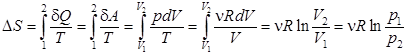. (6.7)

Изменение энтропии в ходе изохорического процесса:

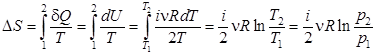. (6.8)

Изменение энтропии в ходе изохорического процесса:

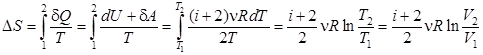(6.9)

Изменение энтропии при адиабатном процессе:

Так как теплота не подводится ( 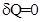), то во всех равновесных адиабатных процессах

DS=0, S=const. (6.10)

Список основных формул

Свойство дискретности электрического заряда: заряд q любого тела кратен элементарному заряду

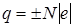, (9.1)

где 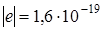Кл – элементарный заряд (минимальный заряд, существующий в природе, им обладают электроны и протоны), N – число избыточных электронов или протонов на теле

Закон сохранения электрического заряда: алгебраическая сумма электрических зарядов частиц замкнутой системы остается постоянной

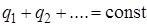. (9.2)

Закон Кулона позволяет вычислить силу электростатического взаимодействия между двумя точечными зарядами:

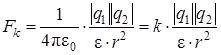, (9.3)

где q₁ и q₂–величины взаимодействующих электрических зарядов; r – расстояние между ними; ε – диэлектрическая проницаемость среды, в которой находятся заряды (ε = 1 для вакуума, и с достаточной степенью точности можно принять ε = 1 для воздуха), 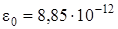Ф/м – электрическая постоянная, 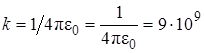Н×м²/Кл².

Напряженность электростатического поля 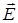– силовая характеристика поля, равная отношению кулоновской 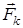силы, действующей на пробный положительный заряд q₀, помещенный в данную точку поля, к величине этого заряда

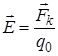. (9.4)

Напряженность E поля, созданного точечным зарядом q

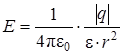(9.5)

Принцип суперпозиции:

- если электростатическое поле создается несколькими зарядами, то вектор напряженности результирующего поля равен векторной сумме напряженностей полей, созданных каждым зарядом по отдельности ( )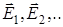

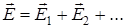(9.6)

- если поле создано макроскопическим заряженным телом, то

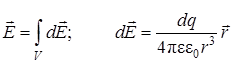, (9.7)

где 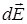– напряженность поля созданного точечным зарядом dq, содержащимся в бесконечно малом объеме тела dV.

Напряженность электрического поля в точке, находящейся на оси заряженного кольца вычисляется по формуле

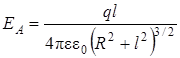, (9.8)

где q – заряд кольца, R – радиус кольца, l – расстояние от центра кольца до точки, лежащей на его оси.

Теорема Гаусса: поток вектора 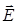через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов 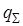, охватываемых этой поверхностью, и деленной на εε₀

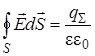, (9.9)

где 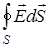– поток вектора напряженности через произвольную замкнутую поверхность S. Если поле создано системой зарядов, то под суммой зарядов следует понимать алгебраическую сумму всех зарядов, охватываемых поверхностью :

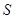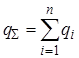. (9.10)

В случае, если заряды распределены непрерывно, то суммарный заряд вычисляется по одной из формул:

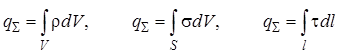, (9.11)

где ρ, σ, τ – объемная, поверхностная и линейная плотности заряда, соответственно; V, S, l –соответственно, объем, поверхность, линия, по которым распределены заряды, охватываемые поверхностью интегрирования.

С помощью теоремы Гаусса можно вычислять напряженности полей созданных различными заряженными телами.

Напряженность поля, созданного бесконечно протяженной заряженной плоскостью с поверхностной плотностью заряда σ:

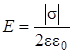, (9.12)

Поле равномерно заряженной (с линейной плотностью заряда τ) бесконечно длинной нити:

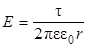. (9.13)

Поле равномерно заряженной по поверхности сферырадиусом R:

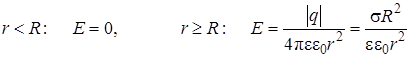, (9.14)

где r – расстояние от центра сферы, до рассматриваемой точки, 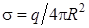– поверхностная плотность заряда на сфере.

Список основных формул

Потенциал φ –энергетическая характеристика поля, равная отношению потенциальной энергии 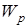пробного заряда 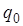, помещенного в данную точку поля, к величине этого заряда

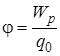(8.1)

Потенциал φ поля, созданного точечным зарядом q

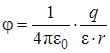, (8.2)

где, r – расстояние от точечного заряда до заданной точки поля.

принцип суперпозиции для потенциала:

- если электростатическое поле создается несколькими зарядами, то потенциал j результирующего поля равен алгебраической сумме потенциалов полей, созданных каждым зарядом по отдельности

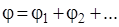(8.3)

- если поле создано макроскопическим заряженным телом, то

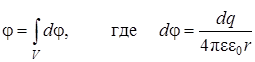, (8.4)

где 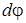– потенциал поля созданного точечным зарядом dq, сосредоточенном в бесконечно малом объеме тела dV.

Потенциальная энергия W_p взаимодействия двух точечных зарядов

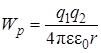, (8.5)

где q₁ и q₂–величины взаимодействующих электрических зарядов; r – расстояние между ними.

Потенциальная энергия W_p системы точечных зарядов ( )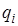

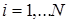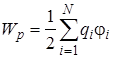, (8.6)

где 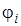–потенциал поля, созданного всеми зарядами, кроме i-го заряда, в месте расположения i-го заряда.

Работа сил электростатического поля по перемещению точного заряда из точки 1 в точку 2может быть вычислена по формулам:

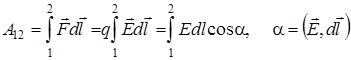; (8.7)

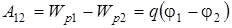, (8.8)

где 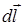- вектор элементарного перемещения, j₁ и j₂ – потенциалы электростатического поля в точках 1 и 2 соответственно.

Связь между напряженностью и потенциалом электростатического поля имеет вид:

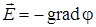(8.9)

В случае радиально-симметричного поля формула (8.9) примет вид:

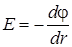, (8.10)

где r – координата точки поля по радиальной оси.

Для однородного поля формула (8.10) принимает вид

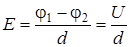, (8.11)

где 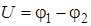– напряжение между точками 1 и 2, а d – расстояние между эквипотенциальными поверхностями с потенциалами j₁ и j₂.

Из выражений (8.7), (8.8) можно получить интегральную формулу связи 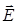иφ, в которую входят две точки поля:

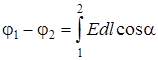. (8.12)

Список основных формул

Электроемкость уединенного проводника – скалярная физическая величина, характеризующая способность проводника накапливать электрический заряд и численно равная

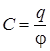, (9.1)

где q – заряд проводника, j – его потенциал.

Электроемкость уединенной металлической сферы

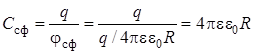, (9.2)

где R – радиус сферы, e – диэлектрическая проницаемость среды, в которой находится проводник.

Электроемкость конденсатора характеризует способность конденсатора накапливать электрический заряд и численно равна

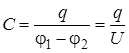, (9.3)

где q – заряд конденсатора, 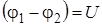– разность потенциалов (напряжение) между его обкладками.

Электроемкость плоского конденсатора

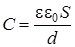, (9.4)

где S – площадь одной пластины конденсатора; d – расстояние, а 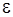– относительная диэлектрическая проницаемость среды между обкладками конденсатора.

Емкость сферического конденсатора

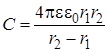, (9.5)

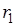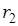где и – радиусы внутренней и внешней обкладок соответственно, ε – диэлектрическая проницаемость среды, заполняющей пространство между обкладками.

Емкость цилиндрического конденсатора

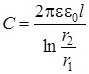, (9.6)

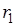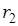где и – радиусы внутренней и внешней обкладок соответственно, l – высота одной обкладки, ε – диэлектрическая проницаемость среды, между обкладками конденсатора.

Энергия уединенного заряженного проводника

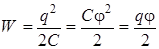, (9.7)

Энергия заряженного конденсатора

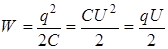. (9.8)

Объемная плотность энергии электростатического поля

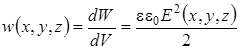, (9.9)

где dW – энергия электростатического поля, заключенная в элементарном объеме dV вблизи точки пространства с координатами (x,y,z), E – напряженность электрического поля вблизи точки с координатами (x,y,z).

Энергия W электрическогополя в любом конечном объеме V пространства может быть рассчитана через объемную плотность энергии w по формуле:

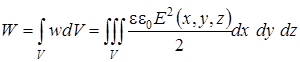. (9.10)

Расчет магнитных полей

Список основных формул.

Закон Био-Савара-Лапласа

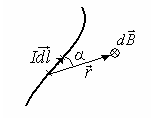
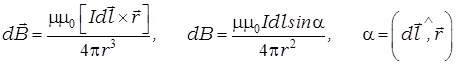. (11.1)

где 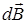– индукция магнитного поля, создаваемого элементом тока 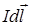; 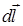– вектор, равный по модулю длине 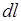проводника и совпадающий по направлению с током, 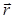– радиус-вектор, проведенный от элемента тока к рассматриваемой точке пространства, 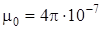Гн/м – магнитная постоянная, m – магнитная проницаемость среды (для вакуума и воздуха m = 1).

Принцип суперпозиции для магнитных полей:

если поле создано проводником с током произвольной конфигурации, то

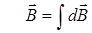, (11.2)

в случае если магнитное поле создается несколькими проводниками с токами, то

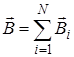. (11.3)

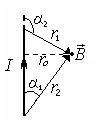Модуль вектора магнитной индукции, создаваемого прямолинейным отрезком проводника конечной длины с током

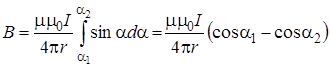, (11.4)

где r – кратчайшее расстояние от рассматриваемой точки до проводника или его продолжения; a₁, a₂ – углы между первым и последним элементами тока и радиус-векторами, проведенных от них в рассматриваемую точку.

Для поля бесконечно длинного прямолинейного проводником с током имеем

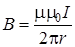, (11.5)

где формула (11.5) является частным случаем (11.4) при α₁→0⁰, α₂→180⁰

Модуль вектора магнитной индукции на оси (В) и в центре (В₀) кольцевого тока

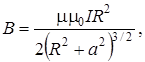(11.6)

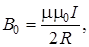(11.7)

где R – радиус кольца; а – расстояние от центра кольцевого тока до рассматриваемой точки, находящейся на оси кольца.

Теорема о циркуляции вектора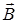

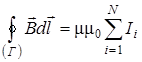(11.8)

Индукция магнитного поля, внутри бесконечно длинного соленоида (длина соленоида значительно больше диаметра витков)

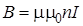, (11.9)

где 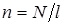– число витков на единицу длины соленоида.

Индукция магнитного поля внутри тороида

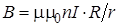(11.10)

где 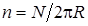– число витков, приходящихся на единицу длины тороида, 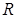– радиус окружности, проходящей через центры витков тороида.

Список основных формул.

Закон Ампера, определяющий силу 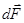, действующую на элемент тока 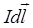со стороны магнитного поля

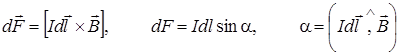. (12.1)

Сила Ампера, действующая на прямолинейный проводник длины l с током I, находящимся в однородном магнитном поле с индукцией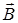

F_A = IBlsina (12.2)

Механический (вращающий) момент, действующий на контур с током, помещенный в однородное магнитное поле,

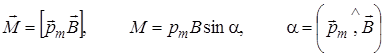. (12.3)

Магнитный момент 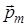контура площади S с током I

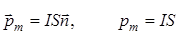, (12.4)

где 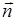– нормаль к контуру (вектор единичной длины, перпендикулярный к плоскости контура, его направление связано с направлением тока правилом правого буравчика).

Потенциальная энергия контура с током в магнитном поле

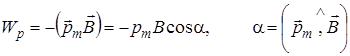. (12.5)

Сила Лоренца, действующая на заряд q, движущийся со скоростью 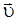в магнитном поле с индукцией :

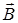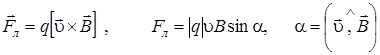. (12.6)

В частном случае, когда заряженная частица влетает перпендикулярно силовым линиям поля, она будет двигаться по окружности в плоскости перпендикулярной силовым линиям поля. Радиус траектории и период обращения заряда в поле равны соответственно

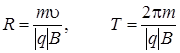. (12.7)

Если частица влетает в магнитное поле под углом 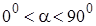к силовым линиям поля, то она будет двигаться по винтовой траектории, параметры которой (радиус R, период Т обращения, шаг h) можно вычислить по формулам:

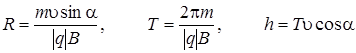. (12.8)

Работа сил магнитного поля по перемещению проводника с током I:

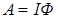, (12.9)

где Ф – магнитный поток, пронизывающий поверхность, которую описывает проводник при своем движении в магнитном поле.

Работа сил магнитного поля при перемещении (повороте) контура с током I:

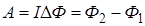, (12.10)

где 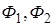– магнитные потоки, пронизывающие плоскость контура в начальном и конечном положениях.

Кинематика и Динамика Вращательного движения

Список основных формул

Угловая скорость ( 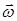) – векторная физическая величина, характеризующая быстроту вращения (поворота), численно равная первой производной вектора углового перемещения по времени:

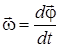(3.1)

Углового ускорения ( 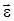) – векторная физическая величина, характеризующая быстроту изменения вектора угловой скорости, численно равная первой производной вектора угловой скорости по времени:

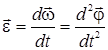(3.2)

Формулы связи кинематических величин поступательного и вращательного движений

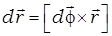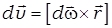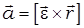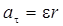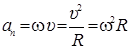; , ; ; (3.3)

Формулы расчета 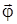и для вращательного движения м.т.

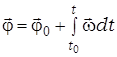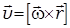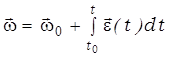, , (3.4)

Момент инерции м.т. и а.т.т. относительно оси вращения – скалярная физическая величина, являющаяся мерой инертности м.т. и а.т.т. при их вращательном движении, численно равная:

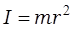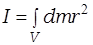и (3.5)

Момент силы относительно оси вращения – векторная физическая величина, равная векторному произведению вектора силы 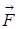и вектора 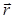, перпендикулярного к оси вращения, и, соединяющего точку приложения силы с осью вращения:

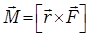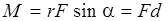, (3.6)

где 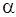– угол между векторам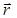и и 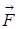, 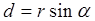– плечо силы (кратчайшее расстояние между осью вращения и линией действия силы);

Основной закон динамики вращательного движения

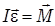(3.7)

Теорема Штейнера:

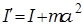(3.8)

где I, I' - моменты инерции тела массы m относительно оси, проходящий через центр масс тела (I) и оси параллельной ей (I'), отстоящей от нее на расстоянии .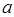

Моменты инерций некоторых тел относительно осей симметрии:

обруч (или тонкостенный цилиндр) массы m и радиуса r:

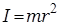(3.9)

сплошной однородный диск (или цилиндр) массы m, радиуса R и высоты h:

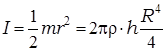(3.10)

где 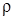– плотность материала диска;

однородный шар массы m и радиуса r

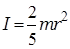(3.11)

тонкий однородный стержень массы m и длины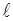

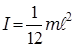(3.12)