Давление жидкости на плоскую наклонную стенку

Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b. Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

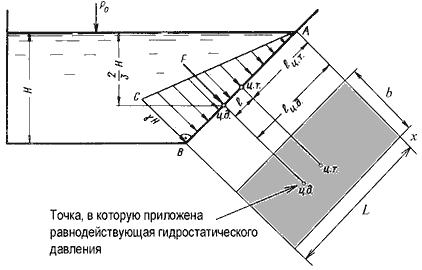
Схема к определению равнодействующей гидростатического давления на плоскую поверхность

Избыточное гидростатическое давление в точке А будет равно:

P_A = γh = γ·0 = 0

Соответственно давление в точке В:

P_B = γh = γH

где H – глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно:

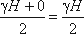
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна:

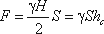
где h_c = Н/2 - глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Если давление p₀ равно атмосферному, и оно действует с обеих сторон стенки, то центр тяжести совпадает с центром давления. Когда же p₀ выше атмосферного, то центр давления находится по правилам механики и эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

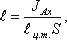
где J_Аx - момент инерции площади S относительно центральной оси, параллельной Аx.

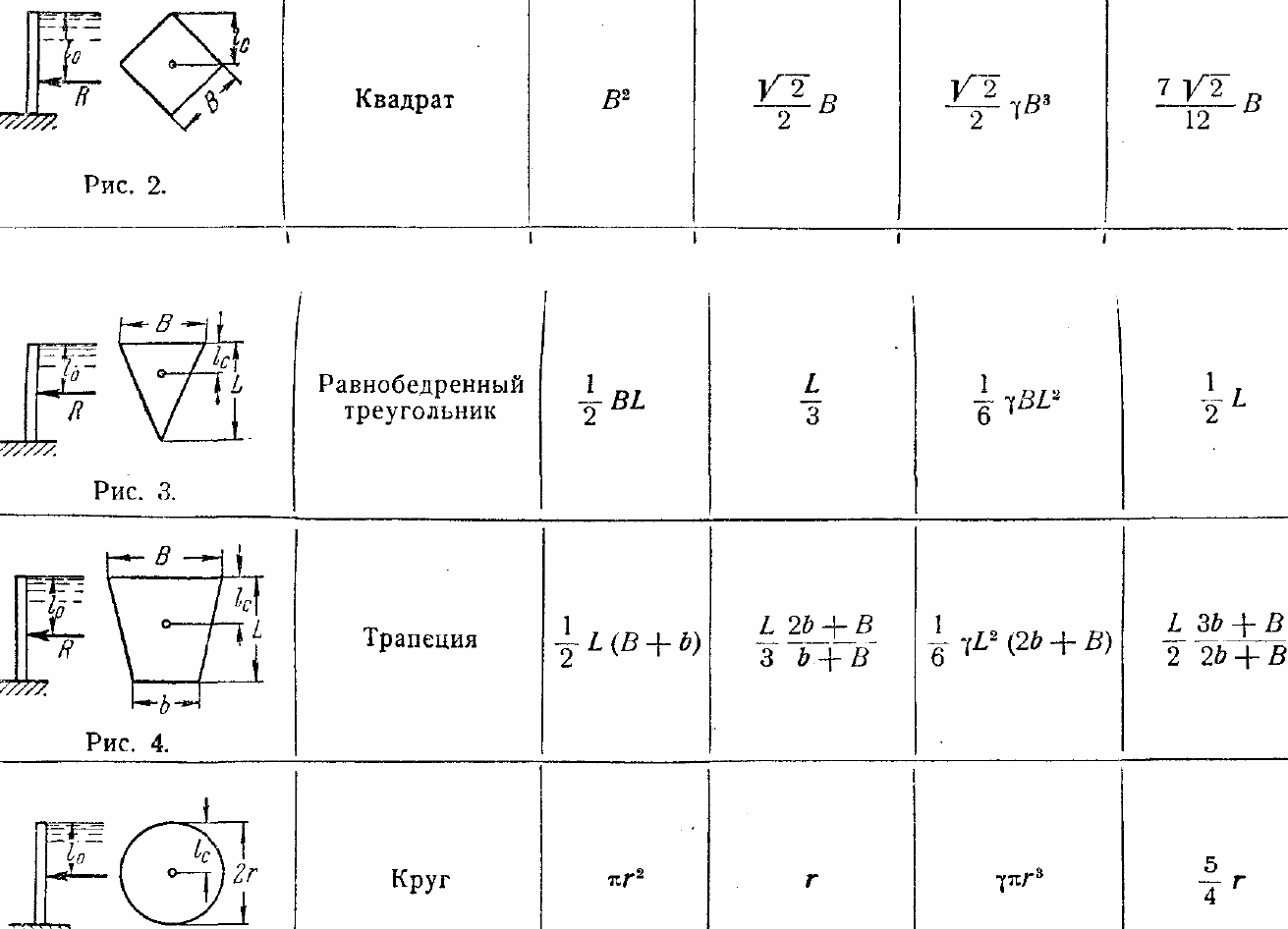
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

ОСНОВЫ ГИДРОДИНАМИКИ

Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

Основные понятия о движении жидкости

Все потоки жидкости подразделяются на два типа (рис. 9):

1) напорные – без свободной поверхности;

2) безнапорные – со свободной поверхностью.

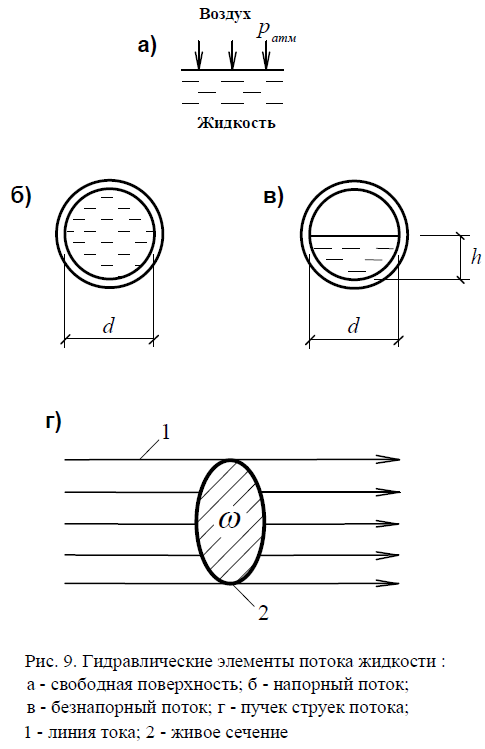
Все потоки имеют общие гидравлические элементы: линии тока, живое сечение, расход, скорость.

Свободная поверхность – это граница раздела жидкости и газа, давление на которой обычно равно атмосферному (рис. 9,а). Её наличие или отсутствие определяет тип потока: безнапорный или напорный. Напорные потоки, как правило, наблюдаются в водопроводных трубах (рис. 9,б) – они работают полным сечением. Безнапорные – в канализационных (рис. 9,в), в которых труба заполнена не полностью, поток имеет свободную поверхность и движется самотёком, за счёт уклона трубы.

Линия тока – это элементарная струйка потока, площадь поперечного сечения которой бесконечно мала. Поток состоит из пучка струек (рис. 9,г).

Живое сечение потока ω (м²) это площадь поперечного сечения потока, перпендикулярная линиям тока (направлению течения).

Например, живое сечение трубы - круг (рис. а); живое сечение клапана - кольцо с изменяющимся внутренним диаметром (рис. б).

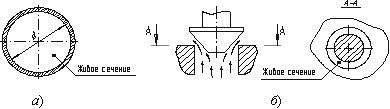
Рис. Живые сечения: а - трубы, б - клапана

Расход потока q (или Q) – это объём жидкости V, проходящий через живое сечение потока в единицу времени t:

q = V/t

Единицы измерения расхода в СИ м³/с, а в других системах: м³/ч, м³/сут, л/с.

Средняя скорость потока V _ср (м/с) – скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω:

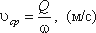
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Скорости потоков воды в сетях водопровода и канализации зданий обычно порядка 1 м/с.

Следующие два термина относятся к безнапорным потокам.

Смоченный периметр χ ("хи") - часть периметра живого сечения, где жидкость соприкасается с твёрдыми стенками. (рис., выделен утолщенной линией).

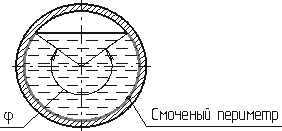
Рис. Смоченный периметр

Для круглой трубы: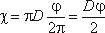

если угол в радианах, или

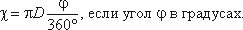
Гидравлический радиус потока R – отношение живого сечения к смоченному периметру:

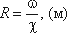
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени:

υ = f(x, y, z)

P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным;

υ = f1(x, y, z, t)

P = φ f1(x, y, z, t)

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное - течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.).