Внутренняя энергия. Аналитическое выражение 1 закона термодинамики

Пусть термодинамическая система массой m занимает объем V при температуре Т и давлении Р. Если из внешней среды (внешнего источника теплоты) к термодинамической системе подводится бесконечно малое количество теплотыdQ, то при определенных условиях температура системы увеличивается на dT. Повышение температуры означает увеличение кинетической энергии Е теплового движения системы на dE_к. В соответствии с уравнением Клапейрона PV = mRT повышение температуры при постоянном давлении внешней среды приводит к увеличению объема системы на dV(рис. 3.2).

В этом случае часть теплоты затрачивается на совершение работы дисгрегации (разъединения) молекул по преодолению сил межмолекулярного сцепления. Увеличение расстояния между молекулами обусловливает возрастание потенциальной энергии системы на величину dE_п.

Суммарное изменение кинетической dE_ки потенциальной dE_п энергии системы составит изменение ее внутренней энергии:

dU = dE_к + dE_п. (2.3)

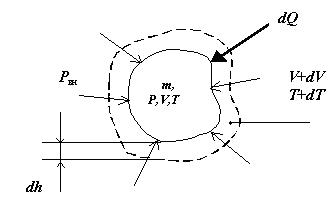
Рисунок 2.2 - К определению работы изменения объема рабочего тела

Внутренняя энергия системы является функцией ее параметров, и, следовательно, функцией состояния. В самом общем виде внутренняя энергия и основные параметры состояния связаны между собой калорическим уравнением состояния

U = F(P, v, T).(2.4)

Внутренняя энергия системы является однозначной функцией двух (из трех) параметров рабочего тела. В зависимости от пары независимых переменных имеем:

U = ¦₁(P, v)

U = ¦₂(v, T) (2.5)

U = ¦₃(P, T)

Термодинамика не занимается определением абсолютного значения внутренней энергии, а рассматривает лишь ее изменение. Так как изменение U не зависит от промежуточных состояний рабочего тела, а определяется только начальным и конечным состоянием системы, то

DU = 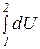= U₂ - U₁(2.6)

Если начальное и конечное состояния совпадают, то 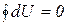(рис. 3.3).

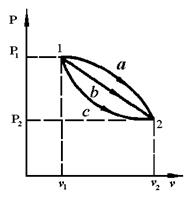
Рисунок 2.3 - Различные изменения состояния газа в процессе 1-2

Изменение внутренней энергии является положительной величиной, если температура термодинамической системы увеличивается. В идеальных газах силы межмолекулярного сцепления не учитываются, в связи с чем dЕ_п= 0 и внутренняя энергия системы изменяется только в зависимости от температуры.

Внутренняя энергия является аддитивным или экстенсивным параметром, так как ее величина зависит от массы тела. Удельная внутренняя энергия сложной системы равна сумме удельных внутренних энергий ее отдельных составляющих, т.е.

U = U₁ + U₂ + ... + U_n = 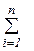U_i (2.7)

При подводе к термодинамической системе количества теплоты не только изменяется внутренняя энергия рабочего тела, но и совершается работа вследствие расширения объема V системы на величину dV при преодолении сил внешнего сопротивления (см. рис.3.3). Для определения этой работы необходимо знать площадь А поверхности, ограничивающей термодинамическую систему, на которую действует внешнее давление Р_вн. При бесконечно малом расширении газа с увеличением температуры на dT каждая точка ограничивающей поверхности переместится на бесконечно малое расстояние dh. Тогда элементарная работа (работа изменения объема или механическая работа) будет равна:

dL = Р_вн^.А^.dh (2.8)

Так как элементарное изменение объема при Р_вн = Р (процесс расширения равновесный), то А^.dh = dV и

dL = PdV (2.9)

Разделив левую и правую части (2.9) на массу, можно получить элементарную удельную работу:

dl = Pdv (2.10)

Элементарная работа dlчисленно равна элементарной площадке под процессом, например, АВ, при изменении объема на dv. Конечная работа

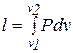, ( 2.11)

где v₁ и v₂ - соответственно начальный и конечный объемы.

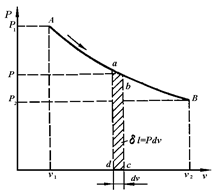
Рисунок 2.4 - vP-диаграмма термодинамического процесса

В координатах vP(рис.2.4) количество работы характеризуется площадью под процессом, т.е. 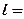пл. v₁ABv₂, а элементарная работа расширения 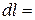пл.abcd. Для подсчета интеграла (2.11) необходимо знать функциональную зависимость Р=¦(v), т.е. термодинамический процесс. Положительная работа совершается при увеличении объема термодинамической системы.

Если рабочее тело совершает круговой процесс, то при собственном расширении тело совершает положительную работу, а при сжатии работа будет отрицательной. Разность абсолютных величин указанных работ дает суммарную работу, совершенную рабочим телом в результате одного кругового процесса или цикла. Она будет численно равна площади внутри замкнутой линии процессов.

Так как подведенное к системе количество теплоты dQ приводит в общем случае к изменению внешней работы dL, на основе закона сохранения энергии можно написать для элементарного процесса:

dQ = dU + dL;

dq = du + dl; (2.12)

q₁₂ = U₂ - U₁+ 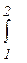Pdv

Из этих уравнений следует, что без подвода теплоты внешняя работа может совершаться только за счет внутренней энергии системы. Уравнения (2.12) являются математическим выражением первого закона термодинамики, которое можно сформулировать следующим образом: подведенная к рабочему телу энергия в форме удельной теплоты расходуется на изменение удельной внутренней энергии тела и на совершение телом внешней работы.

Основные уравнения первого закона термодинамики получены для процессов, в которых единственным видом работы является работа расширения Pdv, но они являются справедливыми для любых систем, как неподвижных, так и перемещающихся в пространстве.

Энтальпия. Энтропия.

В XIX веке в практику тепловых расчетов была введена новая функция, которая названа энтальпией.

Если рассматривать газ, находящийся в цилиндре, и поршень с грузом как одну систему, которую будем называть расширенной системой (рис. 2.5.), то полная энергия 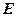этой системы складывается из внутренней энергии газа 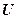и потенциальной энергии поршня с грузом, равной :

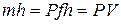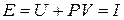[Дж] (2.13)

Рисунок 2.5 - К определению энтальпии газа

Удельная энтальпия, т.е. энтальпия, отнесенная к 1кг рабочего тела, равна:

i = u + Pv [Дж/кг](2.14)

Таким образом, энтальпия i равна энергии расширенной системы - тела и окружающей среды. В этом и заключается физический смысл энтальпии.

Поскольку внутренняя энергия U, давление Р и удельный объем v определяются начальным и конечным состоянием термодинамической системы, энтальпия iтакже является функцией состояния. Энтальпия относится к аддитивным или экстенсивным параметрам, т.к. ее величина пропорциональна массе. Внутренняя энергия идеального газа и произведение Pv в соответствии с уравнением состояния (Pv = RT)зависят только от температуры, поэтому для идеального газа i = ¦(T).

Для оценки изменения энтальпии при изменении состояния термодинамической системы продифференцируем уравнение (2.14).

di = du + Pdv + vdP.(2.15)

Т.к. dL = PdV или dl = Pdv, а dq = du + dl, то

di = dq + vdP (2.16)

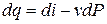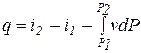, (2.17)

Уравнения (2.17) являются второй формой записи первого закона термодинамики. Произведение 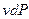в выражении (2.15) в отличие от работы процесса 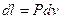, называется располагаемой работой и обозначается через 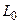(для массы m системы) или l₀(для 1 кг массы системы). Для элементарного и конечного процессов располагаемая работа

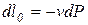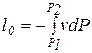, (2.18)

С учетом выражения (2.18) уравнение (2.17) имеет вид:

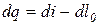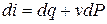, (2.19)

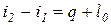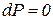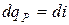или , т.е. энтальпия больше теплоты на величину располагаемой работы. В изобарном процессе и или .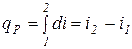

Располагаемая работа газа на 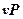-диаграмме (рис.2.6) изображается в виде площади, заключенной между линией процесса, крайними абсциссами и осью давлений 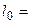пл. 3-4-1-2; элементарная располагаемая работа 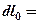пл. abcd.

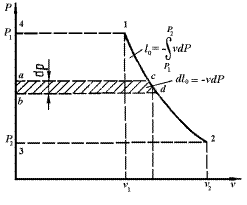
Рисунок 2.6 - К определению удельной располагаемой работы

Располагаемая работа может быть как больше, так и меньше работы расширения и зависит от наклона кривой процесса на vP-диаграмме. Располагаемая работа является положительной величиной при сжатии рабочего тела.

Изменение энтальпии газа в циклах равно нулю, т.е. .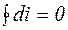

Так как i является функцией состояния, ее изменение во всех процессах, протекающих между точками 1 и 2, будет одинаковым (см. рис.2.3).

Работа, определяемая интегралом

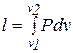(2.20)

совершается рабочим телом в термодинамической системе только тогда, когда изменяется объем.

Обмен энергией может происходить в виде передачи того или иного количества теплоты. Значение 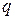, как и 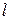, можно подсчитать в виде интеграла, совпадающего по форме с (2.20).

Параметр, который изменяется только от количества переданной теплоты, был предложен Клаузиусом в 1852 году и впоследствии назван энтропией 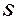[Дж/кг^.К].

Энтропия не может быть измерена каким-либо образом и определяется только расчетным путем. По аналогии с интегралом (2.20) количество теплоты

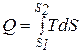или 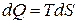. (2.21)

При 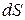> 0теплота к термодинамической системе подводится; при 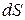<0 - отводится. Удельное количество теплоты через энтропию выражается в виде:

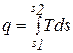или 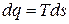, (2.22)

где 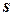- удельная энтропия [Дж/(кг^.К)].

Для подсчета 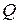или 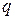необходима функциональная зависимость 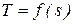так же, как при определении количества работы нужна зависимость .

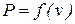Функциональные зависимост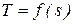и и 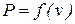определяют термодинамические процессы, поэтому в термодинамике широко используются не только 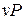координаты, характеризующие совершаемую работу, но и 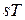координаты, характеризующие теплообмен с внешней средой.

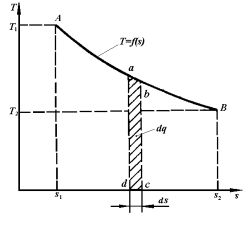
Рисунок 2.7 - 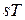-диаграмма термодинамического процесса

В координатах 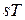(рис.2.7) количество теплоты характеризуется площадью под процессом, т.е. пл. s₁ABs₂, а элементарное количество теплоты 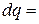пл.abcd.

Т.к. энтропия является функцией состояния, то ее величина определяется значениями параметров состояния 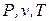, а ее изменение в любом термодинамическом процессе не зависит от характера процесса и определяется только значениями параметров начального и конечного состояний.

Изменение энтропии в каком-либо процессе:

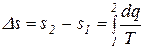. (2.23)

Литература: [2], с. 20-24; [5], с. 4-7, 9-12; [6], с. 13-21; [8], с. 30-38.

Вопросы для самоконтроля

1. Что такое внутренняя энергия? Дайте определение.

2. Дайте формулировку теплоты и работы процесса.

3. Что такое энтальпия и энтропия?

4. В чем разница между функцией состояния и функцией процесса? Приведите примеры этих функций.

5. Когда теплота, работа и изменение внутренней энергии считаются положительными, когда - отрицательными?

6. Как вычислить изменения энтропии идеального газа?