Нормальное распределение и его характеристики

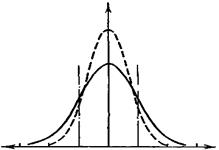
Рассматривая случайные погрешности как один из видов случайных событий, немецкий математик Гаус установил закон распределения погрешностей измерений в зависимости от своей величины. Этот закон называется законом нормального распределения или распределением Гауса. На рисунке 4 приведена кривая, которая отвечает этому закону.

Кривая показывает:

1) наиболее вероятные случайные погрешности, близкие к нулю;

2) с увеличением величины погрешности вероятность их появления быстро уменьшается;

3) погрешности, равные по величине, но противоположные по знаку, ровновероятны;

f(x)

4) при измерениях с одинаковой точностью наиболее возможным значением измеренной величины есть среднее арифметическое из всех результатов.

-3σ -2σ -σ 0 σ 2σ 3σ

Отклонение от действительного значения

Рисунок 4 - График нормального распределения

Кривая нормального распределения отвечает теоретическому случаю бесконечно большого количества измерений n, при котором величины погрешностей неотрывно заполняют всю область значений ±Δх. Аналитическое выражение, которое описывает кривую нормального распределения (закон Гауса) имеет вид:

,

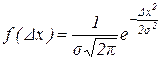где σ² – дисперсия распределения величины Δх.

Из теории следует, что при n >30

,

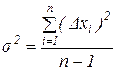где 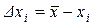- отклонение значения измеренной величины от среднего, которое называется случайной абсолютной погрешностью единичного измерения.

Величину 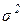называют дисперсией, а 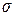- генеральной средне квадратичной погрешностью.

При довольно точных измерениях величина σ мала, а при грубых измерениях наблюдается большой разброс результатов, и значение σ будет большим. В случае реального количества измерений их количество всегда будет конечным. В этом случае не имеет смысла говорить о вероятности появления погрешности данной величины, а говорят о вероятности появления погрешности, которая лежит в пределах некоторого интервала ±Δ_х. Интервал ±Δ_хназывается доверительным, а вероятность Р попадания любого значения измеренной величины в доверительный интервал, называется доверительной вероятностью или надежностью.

Расчеты площадей, ограниченных кривой распределения, для разных 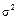дают следующие результаты:

±Δх	≤0,1σ	≤0,5σ	≤σ	≤2σ	≤3σ
Р	0,08	0,38	0,68	0,95	0,98

Для обычных измерений можно ограничиться Р = 0,95. Для измерений, в которых необходимая высокая надежность, задают Р = 0,98.

4.4. Расчет случайной погрешности по методу Стьюдента

В условиях физического практикума тяжело проводить измерение больше 3...5 раз. В этом случае необходимо использовать методику, предложенную в 1908 году английским ученым У. Гассетом (псевдоним - Стьюдент). Он доказал, что статистический подход в достаточной мере возможен и при малом числе измерений (n <30).

Для оценки точности конечного числа измерений вместо σ пользуются выборочным средне квадратичным отклонением среднего арифметического

.

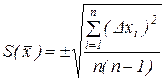Величина, которая равняется отношению

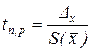
называется коэффициентом Стьюдента. Ниже в таблице 1 приведенные значения коэффициента Стьюдента для любых n и Р

Таблица 1 - Значение коэффициента Стьюдента

P n	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
	0,62	0,82	1,06	1,30	1,90	2,9	4,3	7,0	9,9
	0,58	0,77	0,98	1,30	1,60	2,4	3,2	4,5	5,8
	0,57	0,74	0,94	1,20	1,50	2,1	2,8	3,7	4,6
	0,56	0,73	0,92	1,20	1,50	2,0	2,6	3,4	4,0
	0,55	0,72	0,90	1,10	1,40	1,9	2,4	3,1	3,7
	0,55	0,71	0,90	1,10	1,40	1,9	2,4	3,0	3,5
	0,54	0,71	0,90	1,10	1,40	1,9	2,3	2,9	3,4
	0,54	0,70	0,88	1,10	1,40	1,8	2,3	2,8	3,3
	0,54	0,69	0,87	1,10	1,30	1,8	2,1	2,6	3,0
	0,53	0,69	0,86	1,10	1,30	1,7	2,1	2,5	2,9
	0,53	0,69	0,86	1,10	1,30	1,7	2,1	2,5	2,8
	0,53	0,68	0,85	1,10	1,30	1,7	2,0	2,5	2,8
	0,53	0,68	0,85	1,10	1,30	1,7	2,0	2,4	2,7
	0,53	0,68	0,85	1,00	1,30	1,7	2,0	2,4	2,7