Фазовая скорость, волн де Бройля больше скорости света в вакууме

Конспект лекций 9

ОСНОВЫ ФИЗИКИ АТОМА И ЯДРА

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

Гипотеза де Бройля

Не только фотоны, но и электроны и любые другие микрочастицы обладают одновременно корпускулярными и волновыми свойствами

Количественно связь между корпускулярными (энергия Е и импульс p) и волновыми (частота n и длина волны l.) характеристиками выражаются соотношениями:

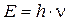
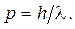
То есть, движение любой микрочастицы, обладающей импульсом (скоростью), сопровождается волновым процессом , длина волны которого определяется по формуле де Бройля:

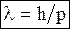
Свойства волн де Бройля

Любая микрочастица массой т, двигаясь со скоростьюV, излучает волны де Бройля.

Фазовая скорость, волн де Бройля больше скорости света в вакууме

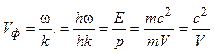
где k=2p/l—волновое число.

Так как c >V, то фазовая скорость больше скорости света в вакууме.

Физика атомов и молекул

Модели атома

Первая модель атома Томсона (однородно положительно заряженная сфера, в которую вкраплены электроны) была признана несостоятельной после опытов Резерфорда по рассеянию 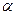-частиц.

Опыт Резерфорда: пучок 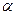-частиц направленный на тонкую золотистую фольгу (Ф) регистрировался после соударения с атомами фольги

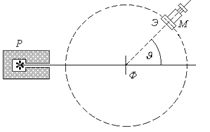Опыты показали, что

Ø некоторые 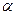-частицы отклонились от первоначального направления,

Ø небольшое количество отразилось от фольги , т. е отклонилось на большие углы (около 180⁰),

Ø а большинство частиц проходило сквозь фольгу, как сквозь пустое пространство.

Выводы Резерфорда: 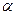-частица может отражаться только от массивного положительного заряда, сосредоточенного в центре атома. Отсюда: планетарная модель атома Резерфорда - весь положительный заряд атома и почти вся его масса сосредоточены в атомном ядре. Вокруг ядра с большой скоростью движутся по круговым орбитам электроны (как планеты вокруг Солнца).

Из модели следует 2 противоречия:

1. Вращаясь, электрон должен испускать свет и терять энергию, т.е. атом должен быть нестабильным (на самом деле атом устойчив);

2. По модели спектр излучения атома должен быть сплошным (на самом деле – атом излучает линейчатый спектр).

Атом водорода в теории Бора

Исходя из идеи Планка о квантовании энергии, Бор на основе модели атома Резерфорда создал свою теорию водородоподобного атома, основанную на трёх постулатах:

Постулаты Бора:

1.Электроны в атоме движутся по стационарным орбитам, среди которых разрешенными являются только те, радиусы которых удовлетворяют условию квантовых значений момента импульса:

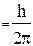
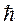
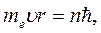(n =1,2,3…)

где - постоянная Планка,

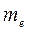- масса электрона,

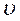- скорость движения электрона по круговой орбите,

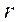- радиус орбиты,

2.Движение электрона по стационарной орбите не сопровождается излучением и поглощением энергии.

3.Испускание и поглощение энергии происходит только при переходе электрона с одной стационарной орбиты на другую.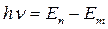

При E_n > E_m – излучение

E_n < E_m - поглощение

Набор возможных дискретных значений частот квантовых переходов определяет линейчатый спектр атомов.

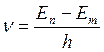
Квантовые числа

В квантовой механике стационарное состояние электрона в атоме водорода определяется тремя квантовыми числами:

· n - главноеквантовое числоопределяет энергетические уровни электрона в атоме, от него зависит радиус орбиты и энергия электрона в атоме

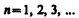
· l - орбитальное квантовое число определяет эксцентриситет орбиты или орбитальный момент импульса L электрона в атоме и может принимать значения

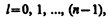
Различные значения l при данном n соответствуют движению электрона по эллипсу различной вытянутости. Совокупность всех электронов по этим эллипсам представляет собой электронный слой (оболочку).

слой K при п = 1

L при п = 2

M при п = 3

· m_і магнитное квантовое число определяет проекцию вектора момента импульса электрона L на заданное направление, зависит от n и l. Может принимать значения

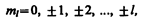
то есть имеет всего (2l+1) значений.

При помещении атома в магнитное поле наличие квантового числа m_lприводит к расщеплению уровня с главным квантовым числом п на (2l+1) подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий (эффект Зеемана).

Энергия

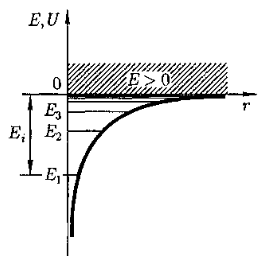Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

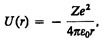(1)

где r — расстояние между электроном и ядром.

Графически функция U(r) изображена на рис. жирной кривой: U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.

Для учета волновых свойств электронов в квантовой механике используют уравнение Шрёдингера. С учетом (1) оно имеет вид:

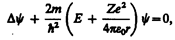(2)

Уравнение (2) имеет решение только при определенных значениях энергии Е и волновой функции Y, которые задаются набором трех квантовых чисел n, l , m.

Другими словами, решение уравнения Шрёдингера содержит в себе три условия квантования, которые дают набор дискретный значений энергии и момента импульса электрона.

Полная энергия электрона в атоме (Е) определяется только главным квантовымчислом п:

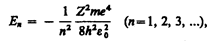(3)

т. е. возможен только дискретный набор отрицательных значений энергии.

Возможные значения энергии электрона на разных уровнях ( Е₁, E₂, Е₃,..) . показаны на рисунке в виде горизонтальных прямых. Самый нижний уровеньэнергии Е₁, —основной, все остальные —возбужденные (Е_n >Е₁, n = 2, 3, ...).

При Е<0 движение электрона являетсясвязанным. Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n=¥ E_¥ = 0.

При Е>0 движение электрона являетсясвободным; область непрерывного спектра Е>0 (заштрихована на рис.) соответствуетионизованному атому. Энергия ионизации атома водорода равна

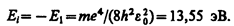(4)

Выражение (3) и величина (4) совпадают с формулой, полученной Бором для энергии атома водорода.

3. Момент импульса

Наличие орбитальных квантовых чисел l и m_і означает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

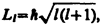
причем вектор Lмомента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации, но лишь такие, при которых его проекция L_lxна направление z внешнего магнитного поля принимает квантованные значения, кратные ћ:

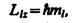
4. Состояния электрона в атоме

Хотя энергия электрона (3) и зависит только от главного квантового числа п, но каждому собственному значению Е_n (кроме Е₁) соответствует несколько собственных функций Y , отличающихся значениями l и m_l.. Так , при данном п орбитальное квантовое число l может изменяться от 0 до (п–1) , а каждому значению l соответствует (2l+1) различных значений m_l .

Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях

Состояния с одинаковой энергией называются вырожденными. Общее число различных состояний с одинаковой энергией называется кратностью вырождения соответствующего энергетического уровня.

Кратность вырождения уровней водорода легко вычислить по формуле

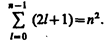
Состояния электрона с различными значениями орбитального квантового числа l принято условно обозначать следующим образом: l = 0 → s- состояние;

l = 1 → p- состояние;

l = 2 → d- состояние;;

l = 3 → f- состояние;;

Условное обозначение состояния электрона начинается со значения главного квантового числа п, далее буква, соответствующая значению l .

1 s,

2 s, 2 p,

3 s, 3 p, 3 d,

4 s, 4 p, 4 d, 4 f,

Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция Y , квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако. Поэтому понятие боровской орбиты радиуса r представляется как состояние электронного облака, имеющего максимальную плотность (густоту) на этих расстояниях r.

Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

5.Спектр

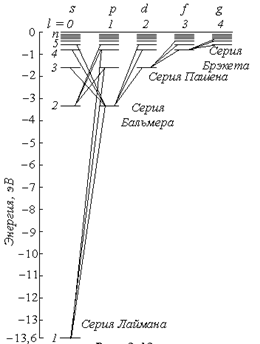
Схему расположения уровней в атоме водорода можно представить, как показано на рис.

В квантовой механике правило отбора для орбитального квантового числа разрешает переходы только на соседние уровни

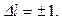
На рис. показаны переходы, разрешённые этим правилом. При каждом переходе излучается или поглощается квант энергии hν. Используя условные обозначения состояний электронов, переходы для серии Лаймана можно представить в виде:

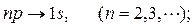
Для серии Бальмера -

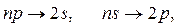
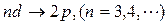
Рентгеновское излучение

Большую роль в выяснении строения атома, а именно распределения электронов по оболочкам, сыграло рентгеновскоеизлучение.

Возникает при соударении электронов, ускоренных высоким напряжением, с металлической мишенью из тяжелых Ме (Pt) внутри рентгеновской трубки.

Рентгеновское излучение – это электромагнитные волны с длиной волны 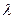от 10^-12 до 10^-8 м.

Спектр содержит 2 компоненты: сплошной спектр (зависит от энергии бомбардирующих электронов) и линейчатый спектр (отдельные max, характеризующие материал анода).

Сплошной спектр, ограничен границей сплошного спектра l_min,со стороны коротких длин волн. Линейчатый спектр это совокупность отдельных линий, появляющихся на фоне сплошного спектра.

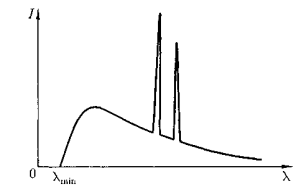Сплошной спектр называется тормозным(т.к. он появляется в результате торможения быстрого электрона при взаимодействии с атомами мишени).

Линейчатый спектр называется характеристическим.

Частота характеристического спектра определяется законом Мозли

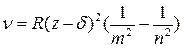
Где: 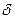- const экранирования;

z – порядковый номер элемента в таблице Менделеева.

Закон Мозли позволяет по измеренной длине волны рентгеновских линий точно устанавливать атомный номер данного элемента.

ЯДЕРНАЯ ФИЗИКА

§1. Заряд, размеры и масса атомного ядра

Атом состоит из положительно заряженного ядра , вокруг которого вращаются электроны.

Ядро атома состоят из элементарных частиц - протонов и нейтронов(нуклонов). В ядре сосредоточено 99,95 % всей массы атома, хотя радиус ядра (10^-14 - 10^-15 м) на 4 - 5 порядков меньше радиуса атома.

Протон- положительно заряженная частица с элементарным зарядом = заряду электрона

р = 1,6·10^-19 Кл. m_p = 1,6726×10^-27 кг.

Нейтрон -электрически нейтрален. m_n = 1,6749×10^-27 кг.

Радиус ядра можно определять соотношением

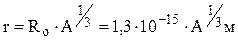
где А – массовое число (число нуклонов в ядре)

Т.к. объем ядра V = 4/3πr³ , то объем ядра V прямо пропорционален числу нуклонов А

§2. Массовое и зарядовое число. Изотопы

Массовое число А = общему количеству нуклонов (протонов+ нейтронов) в ядре.

Зарядовое число Z – это порядковый номер химического элемента в таблице Менделеева

Число протонов в ядре = числу электронов в атоме = Z

Число нейтронов в ядре = A - Z.

Зарядовое и массовое числа принято записывать при символе Х произвольного химического элемента следующим образом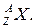

В этих обозначениях протон , нейтрон и электрон обозначают соответственно

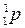
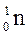
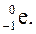
Изотопы– это ядра с одинаковым зарядовым, но с разными массовыми числами (т.е. одинаковое число протонов, но разное число нейтронов)

Например, водород имеет три изотопа 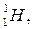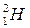(дейтерий) и 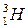(тритий),

Изобарами называются ядра с одинаковым массовым числом, но с разным Z.

Например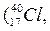

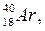
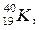
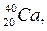
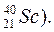
Изотонами называются ядра с одинаковым числом нейтронов.

Например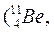

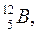
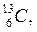
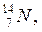
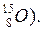
Современные модели ядра

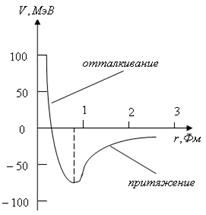
Ядерные силы – новый тип взаимодействий в физике. Ядерные силы оказались гораздо более сложными по сравнению с электромагнитными и гравитационными. Ядерные силы, имеющие характер притяжения на расстоянии ~ 1 ÷ 5 Ферми, сменяются силами отталкивания на расстоянии < 0,5 Ферми.

На рис. показана зависимость потенциальной энергии взаимодействия нуклонов от расстояния между нуклонами. (1Фм = 10^–15м )

Свойства ядерных сил:

1. являются короткодействующими (радиус действия порядка 10^-15 м), на расстояниях, меньших » 0,4 Фм, притяжение нуклонов сменяется отталкиванием;

2. не зависят от заряда нуклона (зарядовая независимость);

3. зависят от взаимной ориентации их спинов, например, протон и нейтрон образуют устойчивый дейтерий только при взаимной параллельности спинов;

4. не являются центральными, что подтверждается зависимостью от ориентации спинов нуклонов;

5. обладают свойством насыщения (каждый нуклон в ядре участвует в сильном взаимодействии с ограниченным числом соседних нуклонов, что подтверждается постоянством удельной энергией связи нуклонов в ядрах и пропорциональностью объёма ядра числу образующих его нуклонов).

Сложный характер ядерных сил не позволил до настоящего времени разработать единую и строгую теорию атомного ядра.

На настоящее время предпочтение отдано следующим моделям ядра:

1. Капельная модель ядра (Бор, Френкель, 1936).

Основано на аналогии между поведением нуклонов в ядре и поведением молекул жидкости в капле.

Эта модель позволила получить формулу для энергии связи в ядре, объяснила механизм ядерных реакций.

Однако она не объясняет повышенную устойчивость ядер, содержащих магические числа протонов и нейтронов.

2. Оболочечная модель ядра (Майер и Йенсен),1950г. Предполагает распределение нуклонов в ядре по дискретным энергетическим уровням (оболочкам), заполняемых нуклонами по принципу Паули. Ядра с полностью заполненными оболочками наиболее устойчивы (магические). Модель объясняет спины и магнитные моменты ядер, различную устойчивость и периодичность свойств.

3. Обобщенная модель – синтез капельной и оболочечной.

4. Оптическая модель – объясняет взаимодействие ядра с бомбардирующими частицами.

Радиоактивное излучение

(лаб. раб. № 702, 703)

Радиоактивность— это испускание ядрами некоторых элементов различных частиц, сопровождающееся переходом ядра в другое состояние и изменением его параметров. Явление радиоактивности было открыто опытным путем французским ученым Анри Беккерелем в 1896 г. для солей урана.

Закон р/а распада

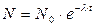
N 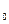-начальное число ядер в момент времени t=0.

N - число не распавшихся ядер в момент времени t.

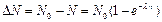- число распавшихся ядер.

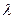- постоянная р/а распада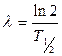

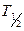- период полураспада – время, за которое распадается половина исходных ядер.

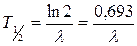
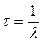среднее время жизни ядра –это промежуток времени, за который число нераспавшихся ядер уменьшается в е раз.

Активность радиоизотопов

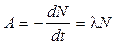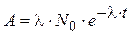или или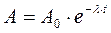

Единица измерения 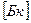- беккерель

Типы ядерных реакций

Деление тяжелых ядер

В настоящее время из всех источников ядерной энергии наибольшее практическое применение имеет энергия, выделяющаяся при делении тяжёлых ядер. В условиях дефицита энергетических ресурсов ядерная энергетика на реакторах деления считается наиболее перспективной в ближайшие десятилетия. На атомных электрических станциях ядерная энергия используется для получения тепла, используемого для выработки электроэнергии и отопления. Ядерные силовые установки решили проблему судов с неограниченным районом плавания (атомные ледоколы, атомные подводные лодки, атомные авианосцы).

Энергия деления ядер урана или плутония применяется в ядерном и термоядерном оружии

(как пускатель термоядерной реакции и как источник дополнительной энергии при делении ядер нейтронами, возникающими в термоядерных реакциях).

Существовали экспериментальные ядерные ракетные двигатели, но испытывались они исключительно на Земле и в контролируемых условиях, по причине опасности радиоактивного загрязнения в случае аварии.

Термоядерный синтез

Энергия термоядерного синтеза применяется в водородной бомбе. Проблема управляемого термоядерного синтеза пока не решена, однако в случае решения этой проблемы он станет практически неограниченным источником дешёвой энергии.

Радиоактивный распад

Энергия, выделяемая при радиоактивном распаде, используется в долгоживущих источниках тепла и бета-гальванических элементах. Автоматические межпланетные станции типа «Пионер» и «Вояджер», а также марсоходы и другие межпланетные миссии используют радиоизотопные термоэлектрические генераторы. Изотопный источник тепла использовали советские лунные миссии «Луноход-1» и «Луноход-2».

Использование атомной энергии создает много проблем. В основном все эти проблемы связаны с тем, что используя себе на благо энергию связи атомного ядра (которую мы и называем ядерной энергией), человек получает существенное зло в виде высокорадиоактивных отходов, которые нельзя просто выбросить. Отходы от атомных источников энергии требуется перерабатывать, перевозить, захоранивать, и хранить продолжительное время в безопасных условиях.

Конспект лекций 9

ОСНОВЫ ФИЗИКИ АТОМА И ЯДРА

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

Гипотеза де Бройля

Не только фотоны, но и электроны и любые другие микрочастицы обладают одновременно корпускулярными и волновыми свойствами

Количественно связь между корпускулярными (энергия Е и импульс p) и волновыми (частота n и длина волны l.) характеристиками выражаются соотношениями:

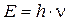
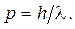
То есть, движение любой микрочастицы, обладающей импульсом (скоростью), сопровождается волновым процессом , длина волны которого определяется по формуле де Бройля:

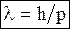
Свойства волн де Бройля

Любая микрочастица массой т, двигаясь со скоростьюV, излучает волны де Бройля.

Фазовая скорость, волн де Бройля больше скорости света в вакууме

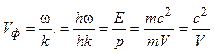
где k=2p/l—волновое число.

Так как c >V, то фазовая скорость больше скорости света в вакууме.