Критерии подобия и уравнения подобия

Помимо безразмерных величин 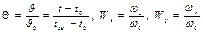и безразмерных координат 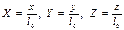, в уравнения конвективного теплообмена входят также безразмерные комплексы, состоящие из разнородных физических величин .

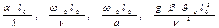Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие теплотехники и механики.

Первый из этих безразмерных комплексов обозначают

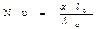и называют числом Нуссельта или безразмерным коэффициентом теплоотдачи.

Число Нуссельта характеризует теплообмен на границе стенка/жидкость. В задачах конвективного теплообмена число Nu обычно является искомой величи­ной, поскольку в него входит определяемая величина α.

Безразмерный комплекс

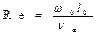называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости.

Третий безразмерный комплекс обозначают

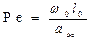и называют числом Пекле.

Его можно преобразовать следующим образом

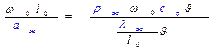
здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.

Безразмерный комплекс

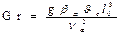называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.

Т.к. при выводе уравнения движения было принято 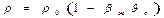-> 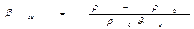, то вместо Gr можно написать его общую модификацию – число Архимеда

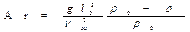
В случае однородной среды при условии β=const число Архимеда идентично числу Gr.

Безразмерные величины Θ, W_х, W_y, X, Y, Nu, Re, Ре, Gr можно рас­сматривать как новые переменные. Их можно разделить на три группы:

- независимые переменные – это безразмерные координаты X, У;

- зависимые переменные – это Nu, Θ, W_x, W_y;

- постоянные величины – это Ре, Re, Gr; они заданы условиями однозначности и для конкретной задачи являются постоянными.

В результате можно написать:

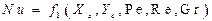
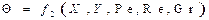
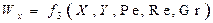
Здесь Х_с, Y_c соответствуют поверхности теп­лоотдачи (стенки).

Безразмерный комплекс

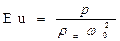называют числом Эйлера. Это число характеризует соотношение сил давления и сил инерции.

В уравнения конвективного теплообмена зави­симая переменная Еu входит только под знаком производной. Следова­тельно, для несжимаемой жидкости с постоян­ными физическими параметрами существенно не абсолютное значение давления, а его изменение. Поэтому число Эйлера обычно представляют в виде:

,

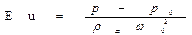где р₀ – какое-либо фиксированное значение давления, например давле­ние на входе в канал.

Очевидно, при неизменной математической формулировке задачи новые безразмерные величины могут быть получены комбинированием старых безразмерных величин.

Число Ре можно представить как произведение двух безразмерных переменных

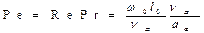
Безразмерная величина 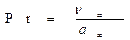представляет собой новую перемен­ную, называемую числом Прандтля. Число Прандтля целиком со­ставлено из физических параметров, и поэтому само является физи­ческим параметром. Его можно записать и в виде:

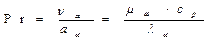
Числу Прандтля можно придать определенный физический смысл.

Уравнение энергии

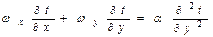, и уравнение движения

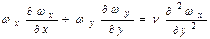по записи аналогичны.

При 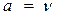расчетные поля температур и скоро­стей будут подобны, если только аналогичны и условия однозначности. Таким образом, при определенных условиях числу Прандтля может быть придан смысл меры подобия полей темпе­ратур и скоростей.

Безразмер­ные переменные можно разделить на два вида:

- определяемые – это числа, в которые входят искомые зависи­мые переменные; в рассматриваемом случае зависимыми являются 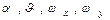, следовательно, определяемыми являются Nu, Θ, W_x и W_y;

- определяющие – это числа, целиком составленные из незави­симых переменных и постоянных величин, входящих в условия однознач­ности; в рассматриваемом случае определяющими являются X, У, Re, Pr (или Ре) и Gr.