Дифференциальные уравнения конвективного теплообмена

Из уравнения

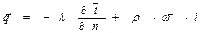следует, что плотность теплового потока в любой точке жидкости для каждого момента времени однозначно определяется, если известны поля температур, удельной энтальпии и скорости.

Связь между температурой и энтальпией может быть установлена следующим образом. Для реальной жидкости 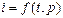, и согласно понятию о полном дифференциале

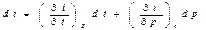
Отсюда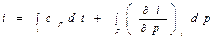

Для многих задач в предположении о несжимаемости жидкости (ρ=const) с достаточной степенью точности можно принять 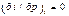, т.е. пользоваться соотношением, справедливым для термодинамически идеального газа:

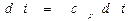и .

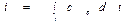Уравнение энергии.

Выведем диф­ференциальное уравнение, описывающее тем­пературное поле в движущейся жидкости.

При выводе будем полагать, что:

- жидкость изотропна,

- её физические параметры постоянны,

- энергия деформации мала по срав­нению с изменением внутренней энергии.

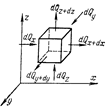
Выделим в потоке жидкости неподвиж­ный относительно координатной системы эле­ментарный параллелепипед с реб­рами dx, dy и dz.

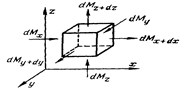Через грани параллелепипе­да теплота переносится теплопроводностью и конвекцией; в общем случае в рассматривае­мом объеме может выделяться теплота внутренними источниками.

Вывод уравнения энергии, соответствующего принятым здесь усло­виям, был получен ранее:

,

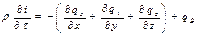Проекции плотности теплового потока 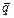на координатные оси Ох, Оу и Оz равны

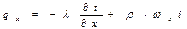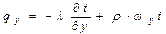, и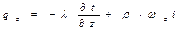

Подставляя значения q_x,q_y и q_z в уравнение Фурье, можно получить

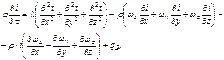
Для несжимаемых жидкостей (ρ=const) из закона сохранения массы следует:

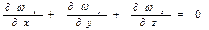
Тогда,

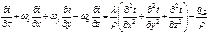
или, если ,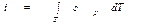

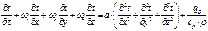
Последнее уравнение является уравнением энергии, описывающим распределение температур внутри движущейся жидкости.

Если 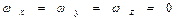, уравнение энергии переходит в уравнение теплопроводности.

Как следует из уравнения энергии, темпера­турное поле в движущейся жидкости зависит от составляющих скорости .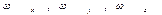

Чтобы сде­лать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали из­менение скорости во времени и пространстве. Такими уравнениями являются дифференциаль­ные уравнения движения.

Уравнения движения.

Уравнение движения вдоль оси Ох

.

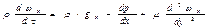Описание движения жидкости усложняется, если скорость изменя­ется по трем направлениям.

для оси Ох

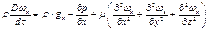
для оси Оу

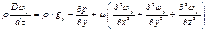для оси Оz

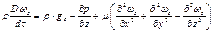В общем случае составляющие скорости изменяются во времени и в пространстве. Член, стоящий в левой части уравнений, представляет собой полную производную от скорости по времени.

На основании понятия о полной (субстанциальной) производной для оси Ох имеем

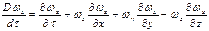
Аналогичные уравнения можно записать и для осей Оу, Оz.

Используя векторную форму записи:

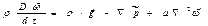
Уравнение движения получено без учета зависимости физи­ческих параметров жидкости от температуры. В частности, не учтена зависимость плотности от температуры.

В то же время свободное дви­жение жидкости определяется разностью плотностей холодных и нагре­тых частиц жидкости.

Приближенный учет переменности плотности возможен с введением температурного коэффициента объемного расши­рения β.

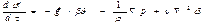
Т.к. в уравнение движения, помимо 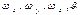входит еще неизвестная величина р, то система уравнений не является замкнутой. Необходимо добавить еще одно уравнение – уравнение сплошности (неразрывности).

Уравнение сплошности.

Выде­лим в потоке движущейся жидкости непо­движный элементарный параллелепипед со сторонами dx, dy и dz и подсчитаем массу жидкости, протекающей через него в на­правлении осей Ох, Оу и Oz за время dτ.

В направлении оси Ох в параллелепи­пед втекает масса жидкости

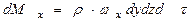
Величина 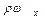представляет собой ко­личество массы, протекающей в единицу времени через единицу поперечного сече­ния. Из противоположной грани вытекает масса

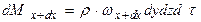
Ограничиваясь первыми двумя членами разложения в ряд, полу­чаем, что масса dM_x+dx, вытекающая из элементарного параллелепида в направлении оси Ох:

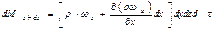Излишек массы жидкости, вытекающий из элементарного объема в направлении оси Ох:

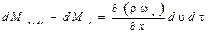
Аналогичным образом можно получить уравнения для направлений по осям Оу и Оz.

Полный избыток мас­сы жидкости, вытекающей из элементарного объема в направлении всех трех осей обуславливается измене­нием плотности жидкости в объеме dυ и равен изменению массы дан­ного объема во времени .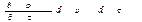

Произведя сокращение на dυ и dτ и перенеся все члены в левую часть равенства, окончательно получим дифференциальное уравнение сплошности для сжимаемых жидкостей

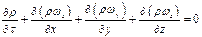Для несжимаемых жидкостей, полагая ρ=const, получаем

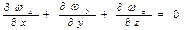
Уравнение сплошности является уравнением сохранения массы.