Потенциальность электрического поля. Потенциал точечного заряда. Расчет напряженности поля и потенциала шара, равномерно заряженного по объему.
Оглавление
1. Электрическое поле. Напряженность поля. Теорема Гаусса и ее применение для расчета поля заряженной пластины.
2. Законы сохранения электрического заряда. Теорема Гаусса (вывод).
3. Потенциальность электрического поля. Потенциал точечного заряда. Расчет напряженности поля и потенциала шара, равномерно заряженного по объему
4. Циркуляция вектора напряженности электрического поля. Расчет напряженности электрического поля и потенциала заряженного цилиндра.
5. Связь напряженности поля и потенциала. Диполь. Расчет напряженности поля и потенциала диполя.
6. Свободные и связанные заряды. Вектор поляризации. Электрическое поле внутри диэлектрика.
7. Полярные и неполярные молекулы. Электронная поляризация. Ориентационная поляризация. Зависимость диэлектрической проницаемости от температуры.
8. Основные характеристики электрического поля в диэлектриках и отклика диэлектрика на воздействие электрического поля: электрическая индукция, поляризация, диэлектрическая восприимчивость и проницаемость.
9. Вектор электрической индукции. Теорема Гаусса для электрической индукции.
10. Граничные условия для векторов напряженности электрического поля и электрической индукции (вывод).
11. Магнитное поле. Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение к расчету поля прямого тока.
12. Вихревой характер магнитного поля. Закон полного тока (вывод) и его применение к расчету поля тороида.
13. Закон полного тока и его применение к расчету поля длинного соленоида.
14. Закон Ампера. Взаимодействие параллельных проводников с током. Контур с током в магнитном поле (момент сил, работа).
15. Магнитный поток. Работа перемещения проводника и контура с током в магнитном поле.
16. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в постоянном и однородном магнитном поле. Эффект Холла.
17. Магнитное поле в веществе и его описание. Вектор намагничивания. Напряженность магнитного поля. Магнитная восприимчивость и магнитная проницаемость. Типы магнетиков.
18. Магнитное поле в веществе. Магнитные моменты и моменты импульса атомов. Спин электрона. Типы магнетиков. Элементарная теория диамагнетизма и парамагнетизма.
19. Ферромагнетизм. Кривая намагничивания. Магнитный гистерезис. Точка Кюри. Домены. Спиновая природа ферромагнетизма.
20. Граничные условия для векторов магнитной индукции и напряженности магнитного поля (вывод).
21. Электромагнитная индукция. Закон Фарадея-Максвелла и его вывод из закона сохранения энергии. Метод измерения индукции Столетова.
22. Явление самоиндукции. Индуктивность. Токи при замыкании и размыкании цепи.
23. Электромагнитная индукция. Явление взаимной индукции. Взаимная индуктивность. Энергия системы проводников с током. Плотность энергии магнитного поля.
24. Дифференциальное уравнение затухающих колебаний (механических и электрических) и его решений. Логарифмический декремент и коэффициент затухания.
25. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс. Резонансные кривые колебательного контура. Добротность.
26. Система уравнений Максвелла в интегральной форме. Материальные уравнения.
27. Система уравнений Максвелла в дифференциальной форме. Волновое уравнение (вывод) для электромагнитных волн.
1. Электрическое поле. Напряженность поля. Теорема Гаусса и ее применение для расчета поля заряженной пластины.
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет св-ва окружающего его пространства – создает в нем электрическое поле.
`Е - напряженность электростатического поля. Векторная величина, основная характеристика электрического поля.
Напряженность поля Е=F/q0 в данной точке пространства явл. физ. вел. численно равная силе действ. в данной точке на единичный неподвижный пробный заряд. Если q0=±1, то `E=`F. [E]=H/Кл [E]=В/м. Напряженность поля системы зарядовравна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности E=SEi – принцип суперпозиции эл. полей;
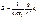Напряженность поля точечного зарядапропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля:
Линии напряженности –силовые линии электрического поля, проводятся так, что касательные в каждой точке, совпадает с направлением поля.
Теорема Гаусса: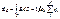 
Поток вектора напряженности эл. поля через замкнутую поверхность равна алгебраической сумме, заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную
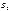
e0=0,885 × 10-11 Ф/м;
Поле заряженной пластины (плоскости):
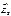
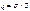
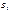
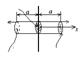
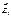Пусть поверхностная плотность заряда во всех точках плоскости одинакова и равна s; для определенности будем считать заряд положительным. Напряженность поля во всех точках имеет направление, перпендикулярное плоскости. Применим к поверхности теорему Гаусса. Суммарный поток через поверхность равен 2EDS. Внутри поверхности заключен заряд sDS. Согласно т. Гаусса должно выполнятся условие: 2EDS=sDS/e0 из которого E=s/2e0.На любых расстояниях от плоскости напряженность поля одинакова по величине. Если взять плоскость конечных размеров, например заряженную тонкую пластинку, то полученный выше результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки.
2. Законы сохранения электрического заряда. Теорема Гаусса (вывод).
З-н сохр. эл. заряда: суммарный заряд электрически изолированной системы не может изменяться.
Вывод Т. Гаусса: Рассмотрим поле точечного заряда q и вычислим поток вектора `E через замкнутую поверхность S, заключающую в себе заряд. Учтя, что количество начинающихся и оканчивающихся на точечном заряде линий численно равно q/e0, можно написать, что ФЕ= q/e0 (1). Знак потока совпадает со знаком заряда q. Размерность обеих частей равенства (1) одинакова. Внутри замкнутой поверхности находится N точечных зарядов q1,q2,…,qN. В силу принципа суперпозиции напряженность E поля, создаваемого всеми зарядами, равна сумме напряженностей Ei, создаваемых каждым зарядом в отдельности: E=SEi. Поэтому:
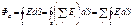
Каждый из интегралов, стоящих под знаком суммы, равен q/e0Þ
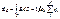
- теорема Гаусса.
Основные характеристики электрического поля в диэлектриках и отклика диэлектрика на воздействие электрического поля: электрическая индукция, поляризация, диэлектрическая восприимчивость и проницаемость.
Вектор электрической индукции (электрическое смещение):
Вектор напряжённости переходя через границу диэлектриков, претерпевает скачкообразное изменение, поэтому поле характеризуют вектором эл. смещения D=e0eE=e0E+P. Вектор D характеризует поле создаваемое свободными зарядами при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
e- относительная диэлектрическая проницаемость среды. (e=1+c)
Условия на границе раздела двух диэлектрических сред:
При переходе через границу раздела двух эл. сред тангенциальная составляющая вектора Е и нормальная составляющая вектора D изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е и тангенциальная D претерпевают скачок.
----------------------------------------------------------------------------------
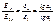
Эффект Холла(1880).
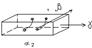
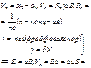
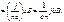
Это возникновение в металле с током плотностью j помещённом в магнитном поле B, электрического поля в направлении перпендикулярном B и j.
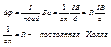
17 Магнитное поле в веществе и его описание, вектор намагничивания, напряжённость магнитного поля, магнитная восприимчивость и магнитная проницаемость.
Спин электрона.
Электрон обладает собственным механическим моментом импульса (спином) Спин является неотъёмлемым свойством электрона подобно заряду и массе. Спину электрона соответствует собственный магнитный момент .
Электрические
рис: свободные э-м колебания-идеальный случай
2.разряд кондера. Благодаря самоиндукции(заключается в появлении ЭДС индукции в самом проводнике при изменении тока в нем.)- ток растет до амплитудного значения. 3.ток , сохраняя направление уменьшается до 0. заряд кондера и разность потенциалов между обкладками-max, но знаки –поменялись. 4.-5. обратный процесс.
колебательный контур=индуктивность+конденсатор+резистор(но его может и не быть , тк каждый контур обладает активным сопротивлением R.) Энергия контура постоянно расходуется на выделение тепла.
Уравнение свободных колебаний:q¢¢+w02q=0: Т=2p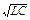 
-период Q(t)=qmcos(w0t+j); Uc= qmcos(w0t+j)/C;Um=Im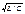 
I(t)=Imcos(w0t+j+p/2)
Уравнение вынужденных колебаний: q¢¢+bq¢+w02q=0
При условии b>w0-затух колебаний нет - апериодические
При условии b<w0-затухающие колебания
Решение уравнения - q(t)=qmе-btcos(wt+j)
Лог декремент: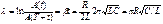 
Q=p/l-ДОБРОТНОСТЬ характеризует колебательную систему, при малых значениях логарифмического декремента
25. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс.Резонансные кривые колебательного контура. Добротность.
Колебания возникающие под действием внешней периодически изменяющейся силы называются вынужденными колебаниями.
1. Механические:
Обозначим:b=h/2m-коэффициент затухания ; w02=k/m-собственная частота свободных колебаний.f0=F0/m
x¢¢+2bх¢+w02х=f0coswt-неоднородное линейное уравнение 2-го порядка
Решение: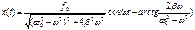 
Электрические
q¢¢+2bq¢+w02q=fmcoswt, fm=Um/l
w 
рез=w02-2b2
Uc=qm/C
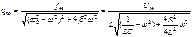
Добротность конденсатора показывает –во сколько раз напряжение на конденсаторе может превысить приложенное.
I(t)=-wqmsin(wt-j)=ImCOS(wt-j+p/2)
Im=qmw=Um/R
Q=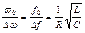 
26. Система уравнений Максвелла в интегральной форме. Материальные уравнения.
1. Закон эл-магн индукции: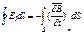 
2. Линии B- замкнуты :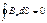 
3. Связь между токами проводимости и смещения и создаваемыми ими уравнениями: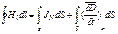 
4. Теорема Гаусса: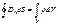 
+материальные уравнения:
1. `D=ee0`E-см далее
2. `B=mm0`H
3. `J=d`E-в-р плотности тока пропорционален напряженности поля
где введены следующие обозначения:
`E- напряженность электрического поля (В / м).
`H- напряженность магнитного поля (А / м).
`D - электрическая индукция (Кл / м2).
`B - магнитная индукция (Т).
r- плотность заряда (Кл / м3).
j- плотность тока (А / м2).
q- электрический заряд (Кл).
I- электрический ток (А).
При рассмотрении полей в различных средах вводятся соотношения между напряжениями и индуктивностями, а также между электрическим током и напряженностью электрического поля Приближенно для линейной, изотропной безинерционной среды можно записать:D=ee0`E
s- удельная проводимость
27. Система уравнений Максвелла в дифференциальной форме. Волновое уравнение (вывод) для электромагнитных волн.
материальные уравнения:
1. `D=ee0`E-вектор электрической индукции пропорционаленнапряженности поля
2. `B=mm0`H
3. `J=d`E-в-р плотности тока пропорционален напряженности поля
`В- вектор магнитной индукции [Тл=Fm/IÙl],
`H- вектор напряженности магнитного поля [А/м]
+Максвелл в дифференциальной форме
1. [Ñ E]=-d B / d t-з-н э-м индукции
2. Ñ B=0-отсустствие магнитных зарядов
3. [Ñ E]=j+ d D / d t-связь токов проводимости и смещения
4. Ñ D=r -источник D -есть сторонние заряды
Оглавление
1. Электрическое поле. Напряженность поля. Теорема Гаусса и ее применение для расчета поля заряженной пластины.
2. Законы сохранения электрического заряда. Теорема Гаусса (вывод).
3. Потенциальность электрического поля. Потенциал точечного заряда. Расчет напряженности поля и потенциала шара, равномерно заряженного по объему
4. Циркуляция вектора напряженности электрического поля. Расчет напряженности электрического поля и потенциала заряженного цилиндра.
5. Связь напряженности поля и потенциала. Диполь. Расчет напряженности поля и потенциала диполя.
6. Свободные и связанные заряды. Вектор поляризации. Электрическое поле внутри диэлектрика.
7. Полярные и неполярные молекулы. Электронная поляризация. Ориентационная поляризация. Зависимость диэлектрической проницаемости от температуры.
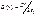8. Основные характеристики электрического поля в диэлектриках и отклика диэлектрика на воздействие электрического поля: электрическая индукция, поляризация, диэлектрическая восприимчивость и проницаемость.
9. Вектор электрической индукции. Теорема Гаусса для электрической индукции.
10. Граничные условия для векторов напряженности электрического поля и электрической индукции (вывод).
11. Магнитное поле. Вектор магнитной индукции. Закон Био-Савара-Лапласа и его применение к расчету поля прямого тока.
12. Вихревой характер магнитного поля. Закон полного тока (вывод) и его применение к расчету поля тороида.
13. Закон полного тока и его применение к расчету поля длинного соленоида.
14. Закон Ампера. Взаимодействие параллельных проводников с током. Контур с током в магнитном поле (момент сил, работа).
15. Магнитный поток. Работа перемещения проводника и контура с током в магнитном поле.
16. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в постоянном и однородном магнитном поле. Эффект Холла.
17. Магнитное поле в веществе и его описание. Вектор намагничивания. Напряженность магнитного поля. Магнитная восприимчивость и магнитная проницаемость. Типы магнетиков.
18. Магнитное поле в веществе. Магнитные моменты и моменты импульса атомов. Спин электрона. Типы магнетиков. Элементарная теория диамагнетизма и парамагнетизма.
19. Ферромагнетизм. Кривая намагничивания. Магнитный гистерезис. Точка Кюри. Домены. Спиновая природа ферромагнетизма.
20. Граничные условия для векторов магнитной индукции и напряженности магнитного поля (вывод).
21. Электромагнитная индукция. Закон Фарадея-Максвелла и его вывод из закона сохранения энергии. Метод измерения индукции Столетова.
22. Явление самоиндукции. Индуктивность. Токи при замыкании и размыкании цепи.
23. Электромагнитная индукция. Явление взаимной индукции. Взаимная индуктивность. Энергия системы проводников с током. Плотность энергии магнитного поля.
24. Дифференциальное уравнение затухающих колебаний (механических и электрических) и его решений. Логарифмический декремент и коэффициент затухания.
25. Дифференциальное уравнение вынужденных колебаний и его решение. Амплитуда и фаза вынужденных колебаний. Резонанс. Резонансные кривые колебательного контура. Добротность.
26. Система уравнений Максвелла в интегральной форме. Материальные уравнения.
27. Система уравнений Максвелла в дифференциальной форме. Волновое уравнение (вывод) для электромагнитных волн.
1. Электрическое поле. Напряженность поля. Теорема Гаусса и ее применение для расчета поля заряженной пластины.
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. Всякий заряд изменяет св-ва окружающего его пространства – создает в нем электрическое поле.
`Е - напряженность электростатического поля. Векторная величина, основная характеристика электрического поля.
Напряженность поля Е=F/q0 в данной точке пространства явл. физ. вел. численно равная силе действ. в данной точке на единичный неподвижный пробный заряд. Если q0=±1, то `E=`F. [E]=H/Кл [E]=В/м. Напряженность поля системы зарядовравна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности E=SEi – принцип суперпозиции эл. полей;
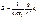Напряженность поля точечного зарядапропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля:
Линии напряженности –силовые линии электрического поля, проводятся так, что касательные в каждой точке, совпадает с направлением поля.
Теорема Гаусса: 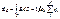Поток вектора напряженности эл. поля через замкнутую поверхность равна алгебраической сумме, заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную
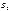
e0=0,885 × 10-11 Ф/м;
Поле заряженной пластины (плоскости):
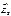
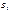
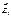Пусть поверхностная плотность заряда во всех точках плоскости одинакова и равна s; для определенности будем считать заряд положительным. Напряженность поля во всех точках имеет направление, перпендикулярное плоскости. Применим к поверхности теорему Гаусса. Суммарный поток через поверхность равен 2EDS. Внутри поверхности заключен заряд sDS. Согласно т. Гаусса должно выполнятся условие: 2EDS=sDS/e0 из которого E=s/2e0.На любых расстояниях от плоскости напряженность поля одинакова по величине. Если взять плоскость конечных размеров, например заряженную тонкую пластинку, то полученный выше результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки.
2. Законы сохранения электрического заряда. Теорема Гаусса (вывод).
З-н сохр. эл. заряда: суммарный заряд электрически изолированной системы не может изменяться.
Вывод Т. Гаусса: Рассмотрим поле точечного заряда q и вычислим поток вектора `E через замкнутую поверхность S, заключающую в себе заряд. Учтя, что количество начинающихся и оканчивающихся на точечном заряде линий численно равно q/e0, можно написать, что ФЕ= q/e0 (1). Знак потока совпадает со знаком заряда q. Размерность обеих частей равенства (1) одинакова. Внутри замкнутой поверхности находится N точечных зарядов q1,q2,…,qN. В силу принципа суперпозиции напряженность E поля, создаваемого всеми зарядами, равна сумме напряженностей Ei, создаваемых каждым зарядом в отдельности: E=SEi. Поэтому:
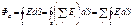
Каждый из интегралов, стоящих под знаком суммы, равен q/e0Þ
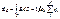
- теорема Гаусса.
Потенциальность электрического поля. Потенциал точечного заряда. Расчет напряженности поля и потенциала шара, равномерно заряженного по объему.
Потенциал – это основная энергетическая хар-ка поля (скалярная). Величина j=Wp/qпр (1) называется потенциалом поляв данной точке и используется, наряду с напряженностью поля E, для описания электрических полей. Из (1) следует, что потенциал численно равен потенциальной энергии, которой бы в данной точке поля положительный единичный заряд. Также, потенциал численно равен работе, которую совершают силы поля над положительным единичным зарядом при удалении его из данной точки на бесконечность. A¥=qj
Потенциал точечного заряда: j=1q/4pe0r [j]=B
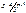Пусть шар R заряжен с постоянной объемной плотностью r. Поле обладает центральной симметрией. Сферическая поверхность радиуса r (r<R) заключает в себе заряд равный:
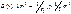
Поэтому т. Гаусса для такой поверхности:1) (r<R)
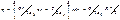
Þ
 |  | ||
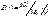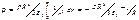2) Þ
Таким образом, внутри шара напряженность поля растет линейно с расстоянием r от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точного заряда.