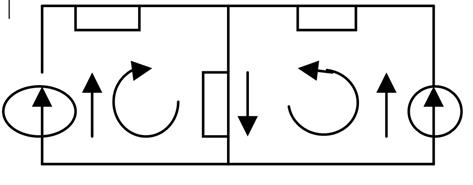
Энергия и мощность. Баланс мощностей.

Электрическая энергия - это способность электромагнитного поля производить работу, преобразовываясь в другие виды энергии.

Электрическая мощность - это работа по перемещению электрических зарядов в единицу времени.

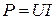
Для любых замкнутых цепей сумма мощностей источников электрической энергии 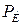, равна сумме мощностей, расходуемых в приемниках энергии 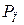: 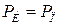. Мощность источников указывает на то, какое количество работы они могут выполнить в электрической цепи каждую секунду. Максимально допустимая мощность приемников это то, что в нормальных условиях может выдержать пассивный элемент.

Мощность, отдаваемая источниками ЭДС, равна.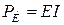

Е — ЭДС источника (В);

I — ток (А), протекающий через этот источник, причем, если положительное направление тока совпадает с направлением ЭДС.

Если в резисторе не происходит химических реакций, то мощность выделяется в форме тепла, согласно известному закону Джоуля.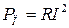

Расчет сложных цепей постоянного тока с помощью законов Кирхгофа.

1) Определяем M, N и К равное

M – Количество ветвей, N – количество узлов, K – количество контуров (контур отличающийся от других контуров хотя бы 1 ветвью)

2) Задаем положительные направления токов в ветвях и положительные направления обхода контуров.

3)составляем систему m-го порядка линейных уравнений на основе закона Кирхгофа, причем на основе 1-го закона Кирхгофа составляем уравнение для произвольных (n-1)узлов.

На основе 2-го закона Кирхгофа составляем недостающие уравнения для независимых контуров.

4) Составленная система линейных уравнений порядка m, решаемая любым из методов линейной алгебры.

Если при решении системы некоторые из рассчитанных токов окажутся отрицательными это будет свидетельством того, что выбранное направление этих токов противоположно заданному направлению.

Пример m=3, n=2, k=2.

Расчет сложных цепей постоянного тока с помощью метода 2-х узлов.

В этом случае задавались направления токов в ветвях и межузловые напряжения

, u – число ветвей содержащие источники

В алгебраическую сумму с «+» вводят слагаемое для ветвей ЭДС которые направлены встречно при которому направлению выше направления . А со знаком «-» наоборот.

После этого находят токи в ветвях на основе: а) закона Ома для участка цепи ветви не содержащих ЭДС

б) на основе закона Ома в полной форме для ветвей, содержащих ЭДС «+» - если ток совпадает с E и U.

Пример:

Находим напряжение.

По закону Ома в полной форме находим токи ветвей:

Метод наложения.

Основан на принципе суперпозиции справедлив для линейных систем. Действительные токи в ветвях электрической цепи, находят как алгебраическую сумму, так называемых частных токов в них, протекающих под воздействием каждой из ЭДС в отдельности : 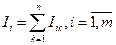;где m-общ.число ветвей, 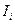-дейст.ток ветви, 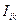-частный ток ветви под воздействием ЭДС. Алгоритм расчета содержит n+1 шагов; на 1,2,..,n-шагах рассчитываются частные соответствующие токи ветвей. На n+1 шагах находятся действительные токи этих ветвей как сумма. Пример : В схеме даны 3 сопротивления , 2 ЭДС. Упрощаем схему находим Rэкв ,зная ЭДС и Rэкв ищем токи, сначала для первой ветви ЭДС, затем для второй, затем суммируем частичные токи для 1и2 ветви, учитывая направление ЭДС и экв-ых токов, тем самым получая общие токи I(1.2.3).