Равновесие плазмы в магнитном поле
Подобно тому как в механике обычной жидкости простейшим случаем является гидростатика, т. е. раздел гидродинамики, изучающий равновесие жидкой или газообразной среды, в магнитной гидродинамике плазмы можно выделить раздел о равновесии плазмы в магнитном поле. В таких состояниях левая часть магнитогидродинамического уравнения Эйлера, описывающая инерцию плазмы, полагается равной нулю, и в результате получается уравнение
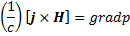 (15.1)
(15.1)
означающее, что сумма объемных сил, действующих на плазму, равна нулю в любой точке внутри плазмы.
Первым следствием условия равновесия плазмы (15.1) является постоянство ее давления вдоль силовых линий магнитного поля, так как [j×H]⊥H. В произвольном случае магнитное поле может иметь довольно сложный характер и свойства равновесного состояния плазмы оказываются непростыми. Задачи такого рода имеют важное значение в проблеме управляемого термоядерного синтеза. Здесь же мы рассмотрим простейший случай равновесия плазмы в магнитном поле с прямолинейными и параллельными друг другу силовыми линиями магнитного поля, иначе говоря, равновесие плазмы в продольном магнитном поле. Магнитное поле имеет только одну компоненту Hz, которая является функцией координат х и у (в плоскости, перпендикулярной к полю). В этом случае условие равновесия принимает вид
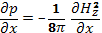
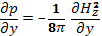 (15.2)
(15.2)
Следовательно,
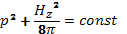 (15.3)
(15.3)
Это соотношение показывает, что магнитное давление H2/8πза пределами области, занятой плазмой, больше, чем внутри нее, на величину pmax. Максимальное давление, при котором плазма может удерживаться полем заданной напряженности H0, определяется из условия
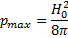 (15.4)
(15.4)
Видно, что магнитное поле внутри плазмы оказывается меньше внешнего поля; это следствие того, что плазма представляет собой диамагнетик. В этом случае плазма должна полностью вытеснять поле из занимаемой ею области пространства.
До сих пор, говоря о равновесии плазмы в магнитном поле, мы использовали лишь одно из уравнений магнитной гидродинамики — уравнение Эйлера, в котором считали du/dt=0. Выясним, совместимо ли это допущение с остальными уравнениями магнитной гидродинамики. Исходя из уравнения
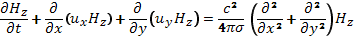 (15.5)
(15.5)
приходим к выводу о неизбежности диффузии магнитного поля внутрь объема, занимаемого плазмой, т. е. в область более слабого поля. Таким образом, магнитное поле, вообще говоря, будет изменяться во времени. Но тогда давление плазмы, жестко связанное с магнитным давлением условием равновесия (15.3), тоже должно меняться, т. е. будет происходить изменение распределения плазмы в пространстве. Этот встречный процесс также имеет диффузионный характер. Коэффициент диффузии плазмы, очевидно, имеет такой же порядок величины, как и 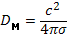 , если давление плазмы сравнимо с давлением магнитного поля
, если давление плазмы сравнимо с давлением магнитного поля 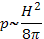 .
.
Уравнение, описывающее процесс диффузии плазмы в магнитном поле при 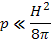 , можно вывести следующим образом. Равновесие плазмы достигается в результате протекания тока плотностью
, можно вывести следующим образом. Равновесие плазмы достигается в результате протекания тока плотностью
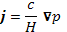 (15.6)
(15.6)
Электрический ток связан с относительным движением электронов и ионов плазмы со скоростью j/en. Электрическое сопротивление такому току есть следствие силы трения между электронами и ионами плазмы:
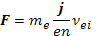 (15.7)
(15.7)
где 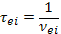 — время свободного пробега электронов по отношению к соударениям с ионами. Точно так же, как рассматривался дрейф заряженных частиц под действием произвольной силы F, можно говорить о дрейфе электронов и ионов под действием силы трения. Скорость такого дрейфа
— время свободного пробега электронов по отношению к соударениям с ионами. Точно так же, как рассматривался дрейф заряженных частиц под действием произвольной силы F, можно говорить о дрейфе электронов и ионов под действием силы трения. Скорость такого дрейфа
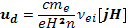 (15.8)
(15.8)
Она одинакова для ионов и электронов, поскольку разные знаки зарядов ионов и электронов компенсируются взаимно противоположными направлениями сил трения. Поэтому в процессе такого дрейфа электрическая нейтральность плазмы не нарушается. Подставим теперь найденную скорость ud движения плазмы под действием сил трения в уравнение, непрерывности. Получим уравнение диффузии
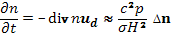 (15.9)
(15.9)
В результате проведенного анализа можно сделать вывод, что в реальном случае плазмы с конечной электропроводностью строгого равновесия не существует, так как скорость плазмы отлична от нуля. Это значит, что инерционный член в уравнении Эйлера, вообще говоря, не обращается в нуль и можно говорить лишь о приближенном выполнении условия равновесия. Это условие выполняется с тем большей точностью, чем меньше относительная величина инерционного члена.
Допустим, что τр — характерное время, за которое происходит изменение плотности плазмы. Тогда сделанное приближение справедливо при условии
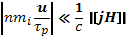
Подставляя u из (15.8), получаем
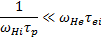 (15.10)
(15.10)
Отсюда видно, что чем выше степень замагниченности плазмы, тем с большим правом можно говорить о ее равновесии.
Из рассмотренной картины диффузии плазмы в магнитном поле вытекает еще одно следствие: диффузия связана со столкновениями между частицами разного сорта — между электронами и ионами (столкновения между одинаковыми частицами в рассмотренном приближении не приводят к диффузии, так как не дают силы трения). Используя уравнение диффузии плазмы (15.9), нетрудно оценить время диффузии (т. е. время, за которое распределение плотности плазмы существенно изменится). Это время
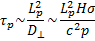 (15.11)
(15.11)
Таким образом, данное равновесие плазмы имеет конечное время жизни порядка τр.
Полезно привести еще один вывод коэффициента диффузии плазмы поперек магнитного поля, рассматривая случайные блуждания частиц вследствие столкновений. За время одного свободного пробега τeiэлектрон в среднем испытывает одно кулоновское столкновение, в результате которого он смещается в плоскости, перпендикулярной к H, на расстояние порядка ларморовского радиуса rHe.При многократных столкновениях согласно статистическим законам складываются квадраты отдельных смещений. Поэтому за время t частица сместится перпендикулярно к H на расстояние
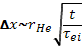 (15.12)
(15.12)
Кроме того, среднее смещение при таком диффузионном процессе должно быть порядка
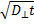 . Следовательно,
. Следовательно,
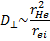 (15.13)
(15.13)
Вследствие квазинейтральности плазмы скорость ее диффузии в направлении, перпендикулярном к H, должна практически совпадать со скоростью диффузии электронов, так как при сравнимых значениях температуры электроны из-за меньшей величины ларморовского радиуса блуждают поперек поля гораздо медленнее, чем ионы. Поэтому формула (15.13) дает оценку коэффициента диффузии для плазмы в целом. Среднее время между двумя столкновениями 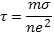 .
.
Поэтому
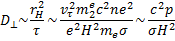 (15.14)
(15.14)
По порядку величины этот результат совпадает с найденным ранее коэффициентом диффузии (15.9).
В диффузию рассмотренного типа дают вклад только столкновения электронов с ионами, но не электронов между собой. Это обстоятельство может ускользнуть от внимания, если ограничиться лишь грубой моделью случайныхблуждений. Вот почему макроскопический подход, основанный на силе трения, особенно полезен. Он автоматически учитывает, что столкновения между электронами не создают средней силы трения, а следовательно, и диффузионного дрейфа.Очевидно, что теплопроводность плазмы в направлении, перпендикулярном к H, также должна резко снижаться при увеличении напряженности поля. В противоположность диффузии, которая обусловлена столкновениями между ионами и электронами, теплопередача в плазме поперек силовых линий происходит в основном в результате ион-ионных столкновений (если Тi не слишком мало по сравнению с Те). Это объясняется тем, что интенсивность теплопередачи зависит от ширины той области, в пределах которой при наличии градиента температуры перемешиваются траектории частиц с различной тепловой энергией. Коэффициент теплопроводностив направлении, перпендикулярном к H, пропорционален квадрату ширины области перемешивания, а эта ширина по порядку величины сравнима с ларморовским радиусом. Поэтому теплопередача в основном идет через ионную компоненту 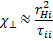 .
.
Отсюда видно, что коэффициент ионной теплопроводности в направлении, перпендикулярном к силовым линиям, уменьшается примерно в (ωHiτii)2раз по сравнению с тем значением, которое он имеет в отсутствие магнитного поля. Коэффициент поперечной теплопроводности для водородной плазмы можно вычислить, пользуясь следующей формулой:
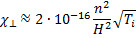 (15.15)
(15.15)
В различных приложениях физики плазмы рассматриваются достаточно сложные типы равновесия плазмы в магнитном поле (так называемые магнитогидродинамические равновесные конфигурации). Однако и в таких произвольных случаях сохраняется основной вывод, сделанный здесь на примере магнитного поля, имеющего только одну компоненту: равновесие имеет условный характер, так как оно с течением времени разрушается из-за диффузии и теплоотвода. В сложных равновесных конфигурациях выражения для коэффициентов диффузии и теплопроводности плазмы поперек магнитного поля могут заметно отличаться от (15.14) и (15.15). Это можно понять, если вспомнить, насколько сложными могут быть дрейфовые траектории электронов и ионов в произвольных магнитных полях. В таких полях в качестве элементарного шага в схеме случайных блужданий частицы может входить величина, намного превышающая ларморовский радиус частицы. Некоторые эффекты такого типа, важные для исследований по управляемым термоядерным реакциям, рассмотрены в параграфе,посвященном токамаку.
Примеры равновесия плазмы в магнитном поле. Токамак
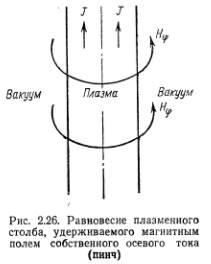 Простейшим конкретным примером применения основных уравнений магнитогидродинамики может служить изолированный плазменный столб цилиндрической формы, удерживаемый магнитным полем протекающего в плазме продольного тока (рис. 2.26). При равновесии радиальный градиент давления в плазменном столбе должен быть равен электродинамической силе (l/c)jzHφ, где jz — плотность продольного тока, а Hφ—напряженность магнитного поля тока. Силовые линии этого поля имеют кольцевую форму. Величины jzи Hφв случае цилиндрической симметрии связаны соотношением
Простейшим конкретным примером применения основных уравнений магнитогидродинамики может служить изолированный плазменный столб цилиндрической формы, удерживаемый магнитным полем протекающего в плазме продольного тока (рис. 2.26). При равновесии радиальный градиент давления в плазменном столбе должен быть равен электродинамической силе (l/c)jzHφ, где jz — плотность продольного тока, а Hφ—напряженность магнитного поля тока. Силовые линии этого поля имеют кольцевую форму. Величины jzи Hφв случае цилиндрической симметрии связаны соотношением
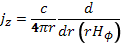
следовательно,
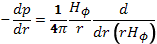 (15.16)
(15.16)
Отсюда
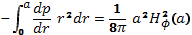 (15.17)
(15.17)
Здесь верхний предел интегрирования по r принят равным радиусу сечения плазменного цилиндра а. На границе плазмы p=0. Поэтому
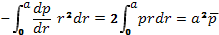 (15.17a)
(15.17a)
где 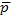 — среднее значение давления плазмы в столбе. Из (15.17) и (15.17а) следует, что
— среднее значение давления плазмы в столбе. Из (15.17) и (15.17а) следует, что 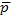 пропорционально квадрату напряженности магнитного поля на границе плазмы:
пропорционально квадрату напряженности магнитного поля на границе плазмы:
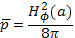
Образование плазменного столба, удерживаемого давлением магнитного поля протекающего по нему тока, носит название линейного пинч-эффекта. При пропускании тока через прямую разрядную трубку, заполненную газом, сначала должна возникнуть плазма (в результате ионизации газа), затем под действием электродинамических сил она начинает сжиматься и в результате может образоваться стянутый к оси плазменный столб. Ток в этом случае выполняет сразу три функции: он создает плазму, нагревает ее за счет джоулева тепла и уравновешивает давление плазмы в сжатом плазменном столбе с помощью давления собственного магнитного поля. В начальный период исследований по физике высокотемпературной плазмы этот метод достижения высоких температур благодаря своей кажущейся простоте представлялся очень перспективным. Казалось, что если пропустить через газ при низком давлении импульсный ток достаточно большой силы, то за ничтожный промежуток времени в разрядной трубке возникнет раскаленный плазменный шнур с огромной температурой.
Однако практически в экспериментах с такой геометрией не удалось поднять температуру плазмы выше ~1*106 К, и то всего лишь на несколько микросекунд. Как показали эксперименты, развитие кратковременного импульсного разряда с большой силой тока не приводит к образованию квазистационарного состояния, описываемого условием равновесия (15.16). Постфактум сейчас можно сказать, что при некоторой проницательности это можно было бы предвидеть заранее. Не учтенным оказался важнейший физический фактор — неустойчивость «гибкого» проводника, каковым является плазменный столб с током. За очень короткий промежуток времени (в обычных условиях эксперимента — за несколько микросекунд) в плазменном шнуре развиваются деформации, напоминающие «перетяжки» и «изгибы» (рис. 2.27). 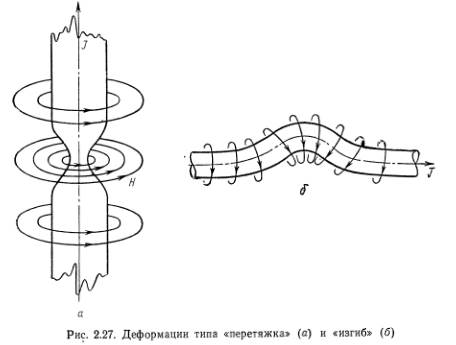 Они разрушают пра- правильную геометрическую структуру плазменного образования, в результате чего плазма начинает сильно взаимодействовать со стенками и быстро охлаждается.
Они разрушают пра- правильную геометрическую структуру плазменного образования, в результате чего плазма начинает сильно взаимодействовать со стенками и быстро охлаждается.
На этом конкретном примере мы впервые встретились с одной из центральных проблем физики плазмы — проблемой устойчивости плазменных конфигураций. Общий анализ относящегося сюда широкого комплекса явлений составит содержание ряда следующих параграфов.
Хотя первая попытка получить высокотемпературную плазму в равновесном состоянии путем использования линейного пинч-эффекта оказалась неудачной, однако дальнейшее развитие этой основной идеи, в конце концов, увенчалось успехом. Два основных элемента, добавленных в процессе развития к первоначальной идее, состояли: 1) в стабилизации неустойчивости «мягкого» плазменного проводника с током при помощи сильного продольного поля внешнего происхождения. Силовые линии продольного поля образуют как бы жесткий каркас, препятствующий нарастанию любых макроскопических деформаций в плазменном шнуре, и 2) в замыкании плазменного цилиндра в кольцо для устранения потерь энергии на концах (при наличии концов, опирающихся на электроды, невозможно получить плазму в квазистационарном состоянии с достаточно высокой температурой).
Итак, мы пришли к системе, получившей название «токамак». Она изображена на рис. 2.28.
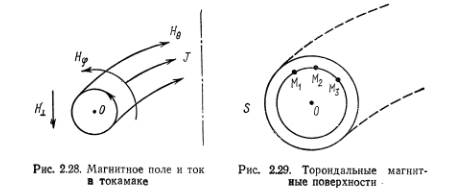 Кольцевой плазменный виток удерживается в равновесии магнитным полем тока Нφи стабилизируется продольным полем Hθ. Ток в плазме можно создать индукционным путем (например, надев камеру, в которой должен образоваться плазменный виток, на сердечник трансформатора). Однако, как нетрудно видеть, для того чтобы добиться равновесия плазмы, кроме полей Нφи Hθнужно ввести также поле Н⊥, направленное вдоль главной оси тороидальной системы (перпендикулярно к плазменному кольцу). Это поле необходимо для того, чтобы скомпенсировать электродинамическую силу радиального расталкивания кольцевого плазменного тока. При взаимодействии поля Н⊥с током I возникает сила
Кольцевой плазменный виток удерживается в равновесии магнитным полем тока Нφи стабилизируется продольным полем Hθ. Ток в плазме можно создать индукционным путем (например, надев камеру, в которой должен образоваться плазменный виток, на сердечник трансформатора). Однако, как нетрудно видеть, для того чтобы добиться равновесия плазмы, кроме полей Нφи Hθнужно ввести также поле Н⊥, направленное вдоль главной оси тороидальной системы (перпендикулярно к плазменному кольцу). Это поле необходимо для того, чтобы скомпенсировать электродинамическую силу радиального расталкивания кольцевого плазменного тока. При взаимодействии поля Н⊥с током I возникает сила 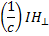 (на единицу плазменного кольца). При указанном на рис. 2.28 направлении Н⊥ эта сила в каждом элементе кольца направлена по радиусу к оси тороидальной системы.
(на единицу плазменного кольца). При указанном на рис. 2.28 направлении Н⊥ эта сила в каждом элементе кольца направлена по радиусу к оси тороидальной системы.
В обычных условиях | Н⊥ | < | Нφ (а)|, поэтому присутствие Н⊥ не нарушает общей картины поля. Линии результирующего магнитного поля имеют винтовую структуру. Они навиваются вокруг кольцевой осевой линии плазменного витка. В таком поле траектории заряженных частиц принадлежат к двум различным классам: существуют «пролетные» и «запертые» частицы. Рассматриваемая как единое целое, плазма свободно растекается вдоль винтовых силовых линий. Прежде чем заниматься анализом условий равновесия в такой тороидальной системе, следует обратить внимание на одну характерную для нее черту топологии магнитного поля. Пусть плоскость S представляет собой поперечное сечение системы. Силовая линия, проходящая через точку М1 на этой плоскости, обходя один раз вокруг тороида, пересечет плоскость S в точке М2, в следующий раз — в точке M3 и т. д.(рис. 2.29). Множество точек М1,M2, М3, ... в общем случае будет бесконечным. Однако для некоторых линий поля оно может быть конечным, и это означает, что такая линия поля замыкается сама на себя. Это так называемые вырожденные линии. К их числу, в частности, принадлежит осевая линия витка, на которой поле тока обращается в нуль. Ее след (см. рис. 2.28) обозначен буквой О.
Поведение силовой линии, многократно обходящей вдоль торо-тороида, определяется положением изображающих точек М1,M2,... Пусть после нескольких обходов точка М приблизилась к начальной точке М1. При следующем обходе угол поворота вокруг Обудет уже больше 2π. Где в таком случае расположится следующая точка? Естественно предположить, что Мn+1 лежит между М1 и М2, следующая Мn+2 — между М2 и М3 и т. д., и после многих обходов изображающие точки образуют гладкую замкнутую кривую. В таком случае можно говорить о существовании семейства магнитных поверхностей. Каждая из них, образно выражаясь, изготовлена из одной бесконечной силовой линии. Линия поля, порождающая магнитную поверхность, плотно устилает ее.
Магнитные поверхности в токамаке образуют множество вложенных друг вдруга тороидов. В континууме этих тороидов каждый, взятый наудачу, образуется одной силовой линией. Однако среди магнитных поверхностей есть счетное множество «вырожденных», которые создаютсязамкнутыми силовыми линиями. В этом случае на поверхности укладывается непрерывное множество линий поля, смещенных друг относительно друга. Л. Спитцер высказал гипотезу о том, что магнитные поверхности существуют также и для таких тороидальных полей, в которых винтовые силовые линии, поворачивающиеся вокруг кольцевой оси, создаются только с помощью внешних источников специальных винтовых обмоток или же деформацией всей магнитной системы — например, превращением кольцевого соленоида в восьмерку (рис. 2.30). 
Однако теоретический анализ показывает, что в случае таких несимметричных полей можно говорить о системе вложенных друг в друга магнитных поверхностей лишь в некотором приближении. В общем случае структура магнитного поля является довольно сложной. Отдельные магнитные поверхности оказываются разделенными системой тороидальных трубок («волокон»), между которыми силовые линии ведут себя совершенно хаотически. Очевидно, что вопрос о существовании магнитных поверхностей имеет большое значение для перспективы использования различных магнитных систем для удержания горячей плазмы. Поскольку плазма свободно растекается вдоль силовых линий, ее давление р в условиях равновесия должно быть одинаковым в разных точках одной и той же магнитной поверхности.
Таким образом, магнитные поверхности представляют собой семейство плазменных изобар. Если (вместо того чтобы обрисовывать плавную кривую) «изображающие» точки М1, М2... заполнят некоторую широкую зону в поперечном сечении плазменного витка, то в пределах этой зоны плазма может находиться в равновесии только при условии gradp=0. Очевидно, что обращение в нуль градиента давления в сечении плазменного витка равносильно появлению аномально большой утечки плазмы в направлении, перпендикулярном к Н.
Представляет немалый интерес хотя бы вкратце разобрать вопрос о топологии магнитных поверхностей. Если заданы источники магнитного поля, т. е. система электрических токов, то вектор магнитного поля Н(r) можно в принципе считать заданным (вычисленным по формуле Био—Савара). Это позволяет написать систему уравнений для силовых линий магнитного поля, используя их определение как линий, касательная к которым параллельна Н в каждой точке. Оказывается, что найти решение этой, казалось бы, простой системы уравнений в общем случае не так-то просто.
Основная идея подхода к этой проблеме заключается в использовании, на первый взгляд, неожиданной аналогии с гамильтоновыми уравнениями динамики материальной точки. В данном случае это означает, что координата вдоль силовой линии играет роль времени, а некий «гамильтониан», описывающий силовые поля, в которых «движется» рассматриваемая материальная точка, тогда должен быть периодической функцией времени. Теперь становится понятной сложность задачи. Ведь в классической механике вопрос об устойчивости движения с такими гамильтонианами сводится к знаменитой проблеме о так называемых малых резонансных знаменателях. Формально разложение в ряд Фурье нелинейной периодической функции содержит бесконечное число членов с потенциальной возможностью соответственно бесконечного числа резонансов.
Весьма сходная проблема небесной механики — о движении планет при учете возмущающего резонансного влияния друг на друга — как известно, приводит к неустойчивости множества возможных орбит и выделению некоторых устойчивых состояний.
«Резонансные» возмущения, нарушающие тороидальную симметрию магнитного поля в токамаке, могут создаваться не только из-за неидеальной геометрии наружных проводников с током, но и в результате внутренних неоднородностей собственного тока, текущего по плазме. Такие неоднородности могут быть и следствием мелкомасштабных неустойчивостей плазмы. В предельном случае достаточно сильных микронеоднородностей поведение силовых линий магнитного поля может напоминать стохастическое движение броуновской частицы. Такое стохастическое разрушение структуры магнитных поверхностей может стать препятствием для длительного удержания плазмы в термоядерных ловушках.
Эти качественные рассуждения можно проиллюстрировать на примере разрушения плоских магнитных поверхностей при наложении мелкомасштабного возмущающего поля. Пусть магнитные силовые линии являются прямыми, лежащими в плоскостях yz. Напряженность этого поля примем постоянной и равной H0. Примем угол между Н0 и осью z зависящим от координаты х. Если при х=0 H0║0z, тo вблизи х=0 простейшей формой такой зависимости может служить 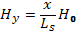 . Физически для реализации описываемого поворота силовых линий нужно иметь электрический ток, текущий вдоль силовых линий по плазме.
. Физически для реализации описываемого поворота силовых линий нужно иметь электрический ток, текущий вдоль силовых линий по плазме.
Наложим возмущающее магнитное поле. Тогда «уравнения движения» для силовых линий с учетом возмущений можно записать в виде, гдеl— координата вдоль силовой линииНо. Интегрируя второе из этих уравнений, получаем 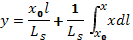 .
.
Выберем хо, удовлетворяющее условию 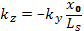 . Оно означает, что возмущение находится «в резонансе» с невозмущенной силовой линией в плоскости х=х0, иначе говоря, фаза возмущения постоянная вдоль l. При этом условии
. Оно означает, что возмущение находится «в резонансе» с невозмущенной силовой линией в плоскости х=х0, иначе говоря, фаза возмущения постоянная вдоль l. При этом условии
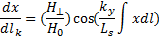 (15.18)
(15.18)
Теперь немедленно воспользуемся аналогией с уравнением движения электрона в поле монохроматической электростатической волны при условии резонанса 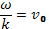 (vo— невозмущенная скорость) :
(vo— невозмущенная скорость) :
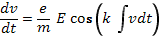
Правила соответствия очевидны:
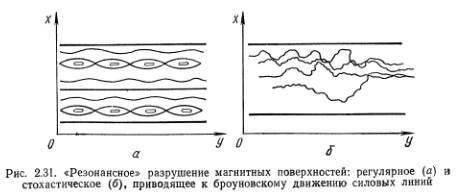 Тогда ширина зоны захвата
Тогда ширина зоны захвата 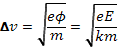 электрона полем волны соответствует ширине зоны резонансного возмущения магнитного поля. Картина возникающего расщепления магнитных поверхностей на плоскости ху в точности совпадает с картиной поведения фазовых траекторий частицы на плоскости vx (рис. 2.31,а). Аналогом осцилляции захваченных; электронов на этом рисунке являются так называемые магнитные островки.
электрона полем волны соответствует ширине зоны резонансного возмущения магнитного поля. Картина возникающего расщепления магнитных поверхностей на плоскости ху в точности совпадает с картиной поведения фазовых траекторий частицы на плоскости vx (рис. 2.31,а). Аналогом осцилляции захваченных; электронов на этом рисунке являются так называемые магнитные островки.
Для возмущения, представляющего собой суперпозицию отдельных гармоник нетрудно провести рассуждения, приводящие к установлению аналога квазилинейного приближения для электронов. Условием применимости такого приближения должно являться перекрытие зон резонансов соседних гармоник возмущения. Это квазилинейное уравнение, которое описывает стохастическое поведение силовых линий магнитного поля (см. рис. 2.31,б), легко написать, пользуясь введенными выше правилами соответствия:
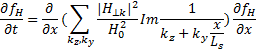
В рассматриваемом приближении «диффузия» силовых линий описывается с помощью соответствующей плотности вероятности fH(l,r).
После этого небольшого отступления проанализируем равновесие кольцевого плазменного витка, используя уравнения магнитной гидродинамики. В первом приближении можно считать, что плазменный виток имеет в поперечном сечении форму окружности радиуса а. Вне этого круга р и j обращаются в нуль. Тороидальнаяповерхность радиуса а представляет собой граничную поверхность плазменного витка, «оторванного» от стенок вакуумной камеры, внутри которой этот виток находится. Вместе с тем это одна измагнитных поверхностей тороидального поля. Другим независимым параметром, определяющим геометрию системы, является большой радиус плазменного витка R. В дальнейшем будем предполагать, что a<<R (это практически всегда выполняется в эксперименте). Заметим, что при малом отношении a/R плазменный виток по свойствам должен приближаться к прямому цилиндру.
Поскольку в задачу входят два главных параметра а и R, отвечающих двум степеням свободы, то нужно найти два условия равновесия витка — по малому и большому радиусам. Для первого можно пренебречь влиянием тороидальности и использовать уравнение равновесия, справедливое для прямого плазменного цилиндра. При этом плазма находится под действием полей Hφ и Hθ, (в первом приближении поле R роли не играет), и поэтому уравнение равновесия должно представлять собой обобщение соотношений (15.16) и (15.17). Такое обобщение можно получить, считая, что напряженность обоих полей и давление плазмы зависят только от r (т. е. от расстояния между данной точкой и точкой О в поперечном сечении). Простые вычисления показывают, что для равновесия необходимо, чтобы соблюдалось следующее равенство:
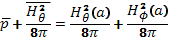 (15.19)
(15.19)
где 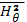 — усредненное значение
— усредненное значение 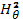 в плазме. Это равенство можно записать также в следующем виде:
в плазме. Это равенство можно записать также в следующем виде:
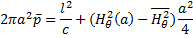 (15.20)
(15.20)
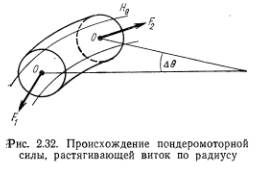 Более детальный анализ приводит к выводу, что соотношение (15.20) справедливо также и для тороидальной системы после внесения небольшого уточнения, которое относится к величине Hθ (а). При строгом расчете Hθ (a) в (15.20) должно соответствовать Hθ на поверхности плазмы при φ=π/2 (рис. 2.32).
Более детальный анализ приводит к выводу, что соотношение (15.20) справедливо также и для тороидальной системы после внесения небольшого уточнения, которое относится к величине Hθ (а). При строгом расчете Hθ (a) в (15.20) должно соответствовать Hθ на поверхности плазмы при φ=π/2 (рис. 2.32).
Выясним теперь происхождение и величину сил, которые могут вызвать изменение R. Существуют следующие причины их появления:
1. Согласно законам электродинамики в кольцевом проводнике с током должна возникать радиальная сила растяжения, пропорциональная I2. При а/R<<1 она равна 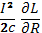 , где L — коэффициент самоиндукции проводника.
, где L — коэффициент самоиндукции проводника.
2. Плазменный виток должен растягиваться также под действием внутреннего давления. Растягивающее усилие можно определить, вычислив работу, совершаемую давлением плазмы при бесконечно малом изменении R, и разделив эту работу на δR. Таким путем нетрудно найти, что полное растягивающее усилие равно .
3. Существует также радиальная пондеромоторная сила, обусловленная различием в напряженности продольного магнитного поля вне и внутри плазмы. Механизм возникновения этой силы можно разъяснить, обратившись к рис. 2.32, на котором изображен небольшой отрезок плазменного витка. Кольцевые силовые линии внутри плазмы стремятся сократиться, вследствие чего возникают силы F1 и F2, приложенные к торцам отрезка. Их равнодействующая направлена внутрь. Как нетрудно установить, она равна 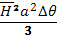 , где ∆θ — угловая длина отрезка. Если бы напряженность поля внутри и снаружи витка была одинакова, то эта сила должна была бы уравновешиваться боковым давлением силовых линий, поэтому результирующая сил бокового давления должна быть равна
, где ∆θ — угловая длина отрезка. Если бы напряженность поля внутри и снаружи витка была одинакова, то эта сила должна была бы уравновешиваться боковым давлением силовых линий, поэтому результирующая сил бокового давления должна быть равна 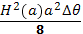 . В общем случае при
. В общем случае при 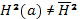 остается разностный эффект. В расчете на всю длину витка он дает силу радиального растяжения, равную
остается разностный эффект. В расчете на всю длину витка он дает силу радиального растяжения, равную
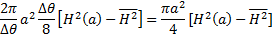 (15.21)
(15.21)
Для равновесия плазменного витка необходимо, чтобы сумма трех радиальных растягивающих усилий компенсировалась силой F⊥ взаимодействия тока I с поперечным полем H⊥. Следовательно, условие равновесия по большому радиусу имеет вид
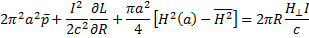 (15.22)
(15.22)
Если плазменный виток создается внутри тороидальной камеры, изготовленной из материала с высокой электропроводностью, то коэффициент самоиндукции можно принять равным
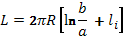 (15.23)
(15.23)
где b — радиус поперечного сечения камеры; li — внутренняя индуктивность плазмы на единицу длины витка (при равномерномраспределении тока по сечению li≈1/4, а при сильном скин-эффекте li≈0). Используя (15.20) и (15.23), можно исключить из уравнения (15.22) член, содержащий 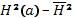 . В результате условие равновесия по R принимает вид
. В результате условие равновесия по R принимает вид
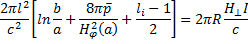 (15.24)
(15.24)
В установках, предназначенных для получения плазменных витков в режимах эксперимента с не очень большой длительностью, компенсация растягивающих усилий может происходить автоматически, так как при радиальном расширении шнура в проводящей оболочке камеры возникают токи Фуко. Они создают поперечную слагающую магнитного поляH⊥, необходимую для компенсации растяжения. Как показывает несложный расчет, составляющая H⊥пропорциональна I и смещению. Итак, равновесие должно устанавливаться при определенном смещении
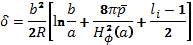 (15.25)
(15.25)
В экспериментальных установках b<<R, и поэтому равновесие устанавливается при относительно небольших смещениях плазмы относительно центра поперечного сечения камеры.
В режимах с большой длительностью компенсация растяжения с помощью токов Фуко оказывается недостаточной, и приходится создавать дополнительные источники поперечных полей, размещая кольцевые проводники с током вблизи камеры. С помощью такихпроводников можно управлять положением витка в камере, изменяя величину δ.
(источник:Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков, гл. 2, §§2.9, 2.10)
Модель двух жидкостей
Ранее проводимость σ вводилась как феноменологическая характеристика плазмы. Чтобы найти ее значение и выяснить физический смысл, необходимо кроме движения плазмы как целого учесть также относительное движение электронов и ионов. Это делается в болеедетальной гидродинамической модели, в которой плазма рассматривается как совокупность двух «жидкостей»: электронной и ионной, — движущихся одна сквозь другую. Электрическое сопротивление плазмы рассматривается при этом как результат взаимного трения этих жидкостей.
Запишем уравнения движения электронов и ионов в виде, аналогичном уравнению (12.2), считая при этом, что на электроны действует только электронное давление ре, а на ионы — только ионное давление рi. Взаимное трение, т. е. передачу импульса при взаимодействии между частицами, учтем введением сил трения Fe и Fi, которые должны удовлетворять третьему закону Ньютона. Удобнее писать уравнения не для скорости, а для импульса. Тогда движение электронов и ионов будет описываться в гидродинамическом приближении системой уравнений
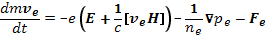 (16.1)
(16.1)
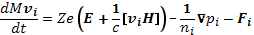 (16.2)
(16.2)
Сила трения, испытываемая электронами, пропорциональна концентрации ионов, а сила трения, испытываемая ионами, — концентрации электронов. Представим эти силы как произведения коэффициента взаимного тренияR на разность скоростей и на концентрацию тормозящих частиц. Тогда система уравнений (16.1)—(16.2) примет вид
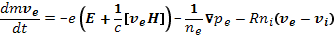 (16.3)
(16.3)
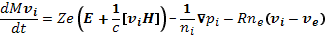 (16.4)
(16.4)
или
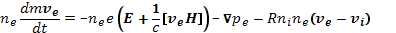 (16.5)
(16.5)
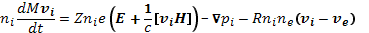 (16.6)
(16.6)
Плазма удовлетворяет условию электронейтральности
 (16.7)
(16.7)
Плотность тока
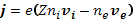 (16.8)
(16.8)
Учитывая условие квазинейтральности(16.7), получаем
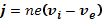 (16.9)
(16.9)
Если сложить уравнения (16.5) и (16.6) с учетом выражений (16.7) и (16.8), то силы электрического поля и трения взаимно уничтожатся. Уничтожение электростатических сил является следствием квазинейтральности, уничтожение сил трения — следствием третьего закона Ньютона. В результате получится уравнение магнитной гидродинамики (12.2), в котором роль скорости течения плазмы v играет средняя массовая скорость
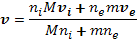 (16.10)
(16.10)
Пренебрегая массой электронов в сравнении с массой ионов, можно считать среднюю массовую скорость не отличающейся от скорости ионов
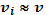 (16.11)
(16.11)
В этом приближении из формулы (16.9) скорость электронов
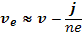 (16.12)
(16.12)
Из законов механики следует, что передача импульса при взаимодействии пропорциональна приведенной массе 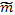 взаимодействующих частиц. Удобно представить коэффициент трения в форме
взаимодействующих частиц. Удобно представить коэффициент трения в форме
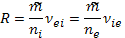 (16.13)
(16.13)
После подстановок выражений (16.12) и (16.13) в систему (16.5)—(16.6) последняя принимает вид
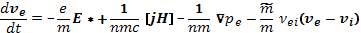 (16.14)
(16.14)
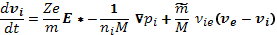 (16.15)
(16.15)
ЗдесьЕ* = Е + (1/с)[vH] — электрическое поле в сопутствующей системе координат (движущейся со средней массовой скоростью плазмы). Величины 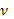 имеют размерность обратного времени, т. е. частоты. Это эффективные частоты передачи импульса от электрона к ионам и от иона к электронам. По аналогии с кинетикой нейтральных частиц, где передача импульса происходит при столкновениях, величины ν часто называют эффективными частотами столкновений. Как видно из определения (16.13), они связаны соотношением
имеют размерность обратного времени, т. е. частоты. Это эффективные частоты передачи импульса от электрона к ионам и от иона к электронам. По аналогии с кинетикой нейтральных частиц, где передача импульса происходит при столкновениях, величины ν часто называют эффективными частотами столкновений. Как видно из определения (16.13), они связаны соотношением
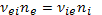 (16.16)
(16.16)
Величину, обратную ν, называют временем передачи импульса
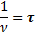 (16.17)
(16.17)
Чтобы иметь полную систему макроскопических уравнений модели двух жидкостей, нужно кроме уравнения для массовой скорости получить также уравнение для плотности тока, которое называют обобщенным законом Ома. В общем случае получение этого уравнения осложняется тем, что субстанциональные (лагранжевы) производные содержатнелинейные члены
