Движение отдельных заряженных частиц и их потоков

Сначала рассмотрим наиболее простой случай дви­жения отдельных заряженных частиц. С известным при­ближением это рассмотрение применимо к потокам ча­стиц, когда плотности их настолько малы, что всяким взаимодействием между частицами можно пренебречь. Например, для слабых пучков электронов или ионов в вакууме можно не принимать во внимание действие их собственного объемного заряда.

Движение отдельной заряженной частицы описывает­ся следующим общим уравнением:

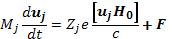(6.1)

где М_j— масса частицы (электрона или иона); Z_j— зарядовое число (для электронаZ_e=—1);
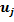— скорость частицы; Н_о— напряженность магнитного по­ля; с—скорость электромагнитных волн в вакууме; F— равнодействующая всех энергетических сил, воз­действующих на частицы (электрических, гравитацион­ных и т. п.).

Воздействие магнитного поля учитывается для удоб­ства отдельно от остальных сил, поскольку оно, дейст­вуя перпендикулярно направлению движения, не изме­няет энергии частиц.

Уравнение (6.1) можно решить лишь в некоторых простейших случаях. Рассмотрим некоторые из них, а затем перейдем к так называемому дрейфовому приближению.

4.2. Движение частиц в электрическом полеE₀

В данном случае уравнение (6.1) запишем

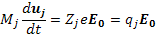(6.2)

где q_j— заряд частицы.

В зависимости от вида поля, т. е. в зависимости его от координат и времени, интегрирование (6.2) дает различные результаты. Рассмотрим некоторые частные примеры, которые пригодятся нам для дальнейшего изложения.

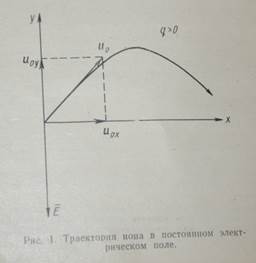
Пример 1. Пусть напряженность поля постоянна как в пространстве, так и во времени (Е₀=const). Найдем траекторию движения иона, влетевшего в это электрическое поле под некоторым углом θ с начальной скоростью u₀. (рис.1)

Интегрируя (6.2), получаем

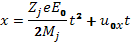(6.3)

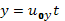(6.4)

где u_0xиu_0y–компоненты начальной скорости. Исключая t, получаем

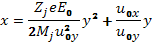(6.5)

Это уравнение параболы. Движение аналогично движению камня, брошенного под углом к горизонту. Это понятно, поскольку электрическое поле и поле тяготения – суть потенциальные.

Пример 2. Электрическое поле однородно в пространстве, но изменяется во времени (для простоты примем гармонический закон изменения E₀). В поле влетает электрон, направление начальной скорости которого перпендикулярно направлению переменного электрического поля. Определим закон движения электрона.

Направим ось у вдоль поля. Тогда

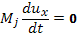(6.6)

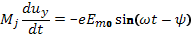(6.7)

Здесь E_m0 – амплитуда напряженности электрического поля; ψ – фазовый угол поля в момент t=0, когда электрон начинает свое движение.

Проинтегрировав (6.6), (6.7), получим

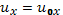(6.8)

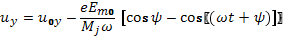(6.9)

где u_0x, u_0y – компоненты начальной скорости электрона. В нашем случае u_0y=0.

Перемещение частицы определяется системой

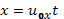(6.10)

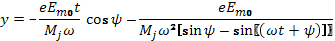(6.11)

Из формул (6.8), (6.9) видно, то происходит стационарный дрейф частиц с постоянной скоростью, на который наложено синусоидальное колебание с амплитудой 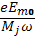(рис.2).

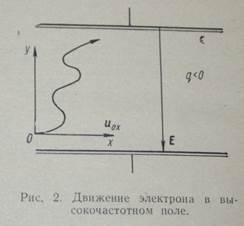Это происходит, например, в высокочастотных разрядах низкого давления или при очень высоких частотах, когда число упругих соударений электронов с молекулами или ионами ν_m намного меньше, чем частота поля ω. Интересно отметить, что в идеальном приближении (ν_m→0) поглощения высокочастотной энергии не происходит, так как колебательная составляющая скорости сдвинута по фазе с полем на угол π/2, а постоянная в разные полупериоды связана то с поглощением энергии, то с отдачей ее обратно полю.

4.3. Движение частиц в магнитном поле Н₀

Если все силы, кроме магнитного поля, отсутствуют, то уравнение движения (6.1) запишемв виде

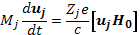(6.3)

Решение этого уравнения зависит, как и в случае электрического шля, отвида правой части. Рассмотрим два примера.

Пример 1. Частица (электрон или ион) с некоторой скоростью u_j влетает в однородное постоянное магнитное поле напряженностью H₀. Необходимо определить закон ее движения.

Разложим полную скорость движения частицы в магнитном поле на две компоненты: u_пр– вдоль поля, u_пер – перпендикулярную к нему:

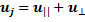(6.13)

Из уравнения (6.12) следует, что

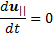(6.14)

Следовательно,

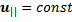(6.15)

т. е. частица вдоль поля движется равномерно. Для другой компоненты

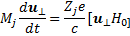(6.16)

Скорость изменения вектора u_перперпендикулярна вектору. В связи с этим изменение этого вектора во времени можно пред­ставить как вращение с некоторой угловой скоростью ω_j

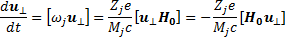(6.17)

Отсюда

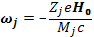(6.18)

Частица равномерно вращается вокруг направления Н₀ с угловой скоростью ω_j, называемой циклотронной или ларморовской частотой, по окружности с ларморовским радиусом,

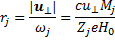(6.19)

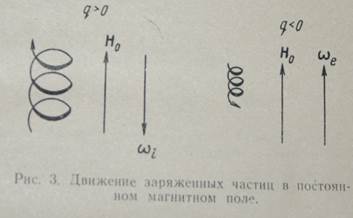Для положительно заряженной частицы угловая скорость ω_jнаправлена против Н₀, для электронов — по вектору Н₀(рис. 3). Из-за большой разности в массах электронов и ионов радиусы их ларморовских окружностей отличаются друг от друга на много порядков.

Периоды обращения по ларморовским окружностям

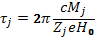(6.20)

Кроме вращения, частица движется поступательно со скоростьюu_пр, следовательно, полное ее движение происходит по винтовой линии, которая навивается на силовую линию поляН_о. Шагэтой винтовой линии

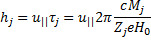(6.21)

При увеличенииН_о, как видно из выражений (6.19) и (6.21), уменьшается радиус ларморовской окружности и шаг винтовой линии, но линейная скорость при этом не меняется.

Циклотронное вращение в постоянном однородном магнитном поле сохраняет свой вращательный момент (момент количества движения)

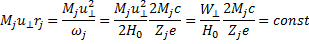(6.22)

где W_⊥– кинетическая энергия циклотронного вращения

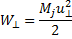(6.23)

Следовательно, и

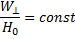(6.24)

Величина W_⊥/H₀ равна магнитному моменту вращающегося в магнитном поле заряда. В самом деле, движение заряда по ларморовской окружности можно рассматривать как круговой ток

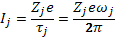(6.25)

его магнитный момент

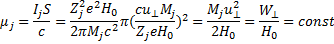(6.26)

где S — площадь ларморовской окружности.

Пример 2. Теперь рассмотрим, что произойдет, если частица влетает в медленно изменяющееся (во времени) магнитное поле.

Под таким полем мы будем подразумевать поле, в котором за один оборот по ларморовской окружности радиус ее почти не меняется:

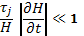(6.27)

Покажем, что и в этом случае магнитный момент 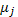приблизительно сохраняет свою величину (в этом случае его называют адиабатическим инвариантом).

Если магнитное поле представляет собой функцию времени, то, как известно, возникает вихревое электрическое поле, циркуляция которого по замкнутому контуру не что иное, как электродвижущая сила (э. д. с).

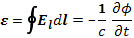(6.28)

где Е_l—напряженность электрического поля вдоль ларморовскойокружности, по которой производится интегрирование; φ— магнитный поток через площадь ларморовского круга.

Изменение энергии циклотронного вращения по времени, учитывая выражения (6.24) и (6.27), равно

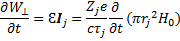(6.29)

При медленном изменении магнитного поля величину 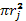можно вынести за знак дифференцирования:

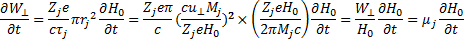(6.30)

Перепишем выражение (6.24) в виде

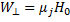(6.31)

и продифференцируем его по времени:

(6.32)

Если сравнить это выражение сполученным ранее непосредственно из энергетических соображений (6.30), то сразу становится очевидным равенство нулю второго члена

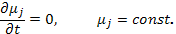
Магнитный поток Ф, пронизывающий циклотронную орбиту, Также остается неизменным в процессе движения

.(6.33)

Дрейфы в магнитных полях

Уравнение движения (6.1) можно решить точно толь­ко в простых случаях, аналогичных уже рассмотренных. При наличии магнитного поля, постоянного во времени и однородного в пространстве, и отсутствии электриче­ских и других сил имеет место движение, которое сла­гается из двух движений — поступательного вдоль по­ля и вращательного в поперечной плоскости. Если маг­нитное поле неоднородно, или на частицу кроме него действуют еще какие-то силы, то такого движения мы уже не получим. Однако в некоторых случаях с извест­ным приближением можно свести реальное движение к вращению частицы по ларморовской окружности, центр которой (так называемый ведущий центр) пере­мещается поперек магнитного поля.

Движение ведущего центра поперек поля называют дрейфом в магнитном поле. Кроме того, при наличии компоненты скорости вдоль направления магнитного поля происходит смещение центра и в этом направле­нии. Такое рассмотрение можно проводить только в случае, когда влияние различных сил проявляется слабо в течение периода обращения частицы в магнитном поле, т. е., иначе говоря, когда выполняются условия адиабатичности (6.27) и (6.34). В этом случае ведущий центр заряженной частицы с магнитным моментом μ_j движется как некая частица в поле силой F с кинетиче­ской энергией W_пер[см. формулу (6.26)].

Приближенная теория движения частиц в адиабати­ческих системах называется дрейфовым приближением, а уравнения, описывающие усредненное движение веду­щего центра и изменение ларморовского радиуса, — дрейфовыми уравнениями. Строгий вывод их довольно сложен. По существу он сводится к рассмотре­нию условий, при которых движение мало отличается от движения в постоянных полях. Действующие силы не должны сильно меняться на протяжении ларморов­ского радиуса, в частности, поперечная сила F_пер не должна приводить к чрезмерному росту поперечных ско­ростей частицы и ларморовского радиуса, что нарушило бы условия адиабатичности. Не может быть большой и продольная сила F_пр. Кроме того, при рассмотрении процессов в плазме, когда применимо дрейфовое при­ближение, не учитывают влияния движения самих частиц на поля, в которых они перемещаются.

Рассмотрим сначала дрейфы в постоянных во време­ни полях. Уравнение (6.1) в проекциях на оси декарто­вых координат:

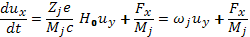
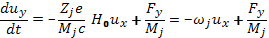(6.38)

Эту систему можно записать в комплексном виде

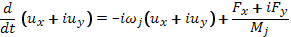(6.39)

Решение неоднородного уравнения (6.39) состоит из общего решения однородного уравнения

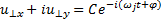(6.40),

котороесоответствует циклотронному вращению, и частного решения

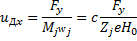(6.41)

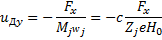(6.42)

В векторном виде

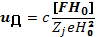(6.43)

Это и есть скорость дрейфового движения, происхож­дение которого можно наглядно пояснить следующим образом: сила в течение одной половины периода цикло­тронного вращения действует вдоль направления дви­жения частицы, скорость ее возрастает и она должна пройти больший путь, чем за вторую половину периода, когда сила действует против движения.

Как уже было сказано, дрейфовое уравнение (6.43) описывает усредненное движение ведущего центра приблизительно с постоянной скоростью. Быстрое ос­циллирующее движение по ларморовской окружности при этом не принимается в расчет. Следует отметить, что дрейфовое движение (перемещение осциллирующего центра) на первый взгляд обладает рядом свойств, как бы нарушающих привычные представления о законах механики. Действительно, постоянная сила в данном случае вызывает не равномерно ускоренное, а равно­мерное движение. В дальнейшем увидим, что электри­ческое поле не разделяет заряды, а заставляет их дви­гаться в одном направлении, в то время как силы не­электрического происхождения создают электрические токи. Дело в том, что истинным движением все же яв­ляется движение по ларморовской окружности, которое связано с отбором (и отдачей) энергии и подчиняется обычным законам механики.

Дрейфовое же движение представляет собой усред­ненное движение, как следствие циклотронного враще­ния в магнитных полях.

Электрический дрейф

Оба вида дрейфа в неодно­родном магнитном поле зависят от знака частиц. От них отличается в этом отношении электрический дрейф, т. е. дрейф ча­стиц в магнитном поле при на­личии электрического. Скорость электрического дрейфа

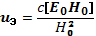(6.47)

Действительно, электрический заряд в формулу не входит, а с ним исключается зависимость скорости от знака частиц. Электрический дрейф для ионов и для электронов происходит в одну сторону и с одинаковой скоростью, несмотря на большое различие в их массах.

Следует иметь в виду, что формула (6.47) примени­ма только при Е₀<<Н₀, иначе скорость дрейфа получается соизмеримой со скоростью света. Весь же наш вы­вод для дрейфовых скоростей сделан исходя из по­стоянства массы частиц, т. е. для нерелятивистских ско­ростей.

Формулу (6.47) мы получили, подставив в общее вы­ражение (6.43) для скорости дрейфов в магнитном поле значение электрической силы

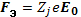(6.48)

Однако ее можно вывести несколько иначе — из об­щего уравнения (6.1). Это целесообразно, если учитывать некоторые полученные полезные физические вы­воды.

Преобразуем уравнение (6.1) в систему отсчета, ко­торая движется относительно исходной (лабораторной) системы координат с постоянной скоростью u'_Д. Ско­рость частицы в движущейся системе u', имлульср'. Скорость в лабораторной системе координат

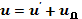(6.49)

Импульс

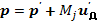(6.50)

Найдем изменение импульса р:

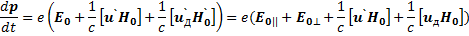(6.51)

где Е_0||и Е_0⊥,—слагающие электрического поля вдоль и перпендикулярно магнитному полю.

Величинуu'_Д можно выбрать таким образом, чтобы выполнялись два условия:

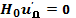(6.52)

и

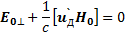(6.53)

Условия (6.52) и (6.53) определяют u'_Дсовершенно однозначно. Из условия (6.52) сразу же следует, чтоu'_Д⊥Н₀. Умножим второе условие (6.53) векторно наН_о:

(6.54)

Член H₀/c·(u'_ДН₀₎=0 согласно условию (6.52). Следовательно,

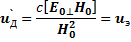(6.55)

т.е. представляет собой дрейфовую скорость. Уравнение движения (6.51) при учете (6.53) запишем

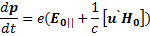(6.56)

Из него полностью выпала компонента E_0пер. Отсюда можно сделать вывод, что влияние E_0пер сводится к созданию дрейфа в направлении, перпендикулярном к магнитному полю. Таким образом, получаем равномерно ускоренное движение вдоль поля и дрейфовое поперек него. Оба движения складываются в движение по па­раболе (рис. 8 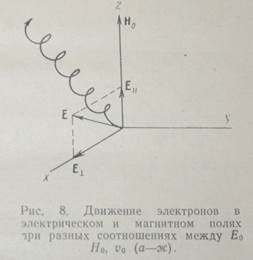). Если Е₀ лежит в плоскости уz, то и ведущий центр не выйдет из этой плоскости. Поскольку выбор осей х и у произволен, случай, показанный на рис. 8, можно считать довольно общим.

Дрейф в скрещенных полях

Частным случаем электрического дрейфа является движение в скрещенных электрическом н магнитном полях (E_o┴H_o и u_0пр=0), где u_0пр — начальная скорость частицы вдоль направленияН_о. Ускорение в направлении Н₀ отсутствует. Частица движется по циклоиде, нормальной или укороченной, в зависимости от соотно­шения между угловой скоростью ω_j и скоростью движения центра самой окружности. Последняя зависит от E₀ и начальной скорости u₀=u_0пер вдоль оси у.

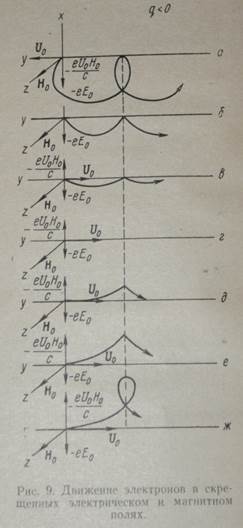Разберем подробнее характер движения в скрещенных полях, поскольку этот случай имеет практическое назначение, особенно для плазменных ускорителей. Рассмотрим движение электрона, а затем определим, в чем состоит отличие для ионов. Нарис. 9, а показано, что происходит, если начальная скорость u₀>0. В этом слу­чае возникает лоренцева сила

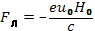(6.57)

направленная антипараллельно оси х. К электрической силе —еЕ₀ добавляется магнитная F_л. Они ускоряют ча­стицу совместно. За ларморовский период τ_е она долж­на пройти большее расстояние, чем при действии только одной —еЕ₀. Это воздействие на частицу определяет движение ее по удлиненной циклоиде.

На рис. 9,б приведен случай, соответствующий на­чальной скорости u₀=0. При этом получается нормаль­ная циклоида. Далее, если u0<0и 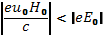, циклоида становится укороченной (рис. 9, в). При уравновешивании обеих сил 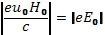траектория остается прямолинейной (рис. 9, г). При дальнейшем увеличении u₀ траектория переходит на правую сторону оси х, причем повторяются в обратном порядке те же формы циклоид — укороченная, нормальная и удлинен­ная (рис.9,д — ж). Расстояние между последователь­ными вершинами циклоид

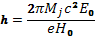(6.58)

Это расстояние не зависит от величины первоначальной скорости u₀.

Для ионов дрейф осуществляется в том же направ­лении, однако вращение происходит в противоположную сторону (рис. 10—сплошные линии). Нетрудно видеть, что дрейф в скрещенных полях происходит по эквипо­тенциальным поверхностям электрического поля, поскольку он направлен по нормали к электрическому полю.