Связь между линейной и угловой скоростью.
Пусть за малый промежуток времени Dt тело повернулось на угол Dj (рис. 2.17). Точка, находящаяся на расстоянии R от оси, проходит при этом путь DS = R×Dj. По определению линейная скорость точки будет равна
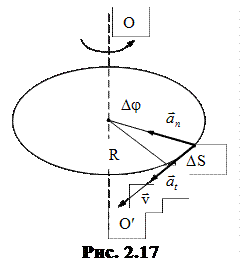
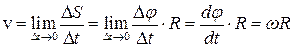 .
.
Итак, v = w·R и чем дальше отстоит точка от оси вращения, тем с большей линейной скоростью она движется.
Найдем теперь линейное ускорение точек вращающегося тела. Нормальное ускорение равно
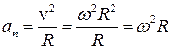 . Итак,
. Итак, 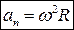
Модуль тангенциального ускорения 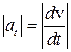 .
.
Отсюда
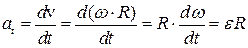 .
.
Итак,
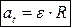 (2.7)
(2.7)
Таким образом, как нормальное, так и тангенциальное ускорения растут линейно с увеличением R (R – расстояние от точки до оси вращения).
Полученное ранее уравнение v=wR устанавливает связь между модулями векторов 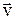 и
и 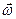 . Пользуясь специальным математическим аппаратом («векторное исчисление») можно установить связь между самими векторами.
. Пользуясь специальным математическим аппаратом («векторное исчисление») можно установить связь между самими векторами.
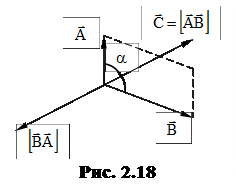 Известно: векторным произведением двух векторов
Известно: векторным произведением двух векторов 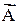 и
и 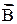 называется вектор
называется вектор 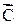 (обозначение:
(обозначение: 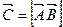 ), обладающий следующими свойствами:
), обладающий следующими свойствами:
1. Модуль вектора 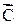 равен произведению модулей перемножаемых векторов на синус угла a между ними (рис. 2.18).
равен произведению модулей перемножаемых векторов на синус угла a между ними (рис. 2.18).
2. Вектор 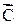 перпендикулярен к плоскости, в которой лежат вектора
перпендикулярен к плоскости, в которой лежат вектора 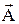 и
и 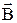 , причем направление его связано с направлениями
, причем направление его связано с направлениями 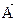 и
и 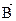 по правилу правого винта: если смотреть вслед вектору
по правилу правого винта: если смотреть вслед вектору 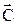 , то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке.
, то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке.
Пусть тело вращается вокруг оси Z с угловой скоростью w (рис. 2.19). Легко видеть, что векторное произведение 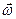 на радиус–вектор
на радиус–вектор 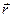 точки, скорость
точки, скорость 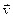 которой мы хотим найти, представляет собой вектор, совпадающий по направлению с вектором
которой мы хотим найти, представляет собой вектор, совпадающий по направлению с вектором 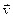 и имеющий модуль, равный w×r×sina=w×R, т.е. v.
и имеющий модуль, равный w×r×sina=w×R, т.е. v.
Таким образом, векторное произведение
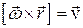 .
.
Иногда применяют другие обозначения векторного произведения
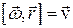 или
или 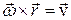
Учитывая, что 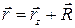 , получим
, получим
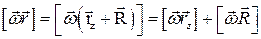
Первое слагаемое в последнем выражении равно нулю, т.к. sina = 0. Следовательно, 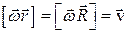 .
.
Итак,
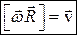 , (2.8)
, (2.8)
где 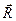 - перпендикулярная к оси вращения составляющая радиус-вектора
- перпендикулярная к оси вращения составляющая радиус-вектора 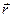 , проведенного из точки, взятой на оси.
, проведенного из точки, взятой на оси.
Модулю векторного произведения можно дать простую геометрическую интерпретацию: выражение AB·sina численно равно площади параллелограмма, построенного на векторах 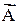 и
и 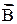 (рис. 2.20), вектор
(рис. 2.20), вектор 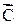 в этом случае ^ плоскости чертежа и направлен за чертеж.
в этом случае ^ плоскости чертежа и направлен за чертеж.
|

| ЛЕКЦИЯ 3 |
Динамика
Раздел механики, исследующий законы и причины, вызывающие движение тел, т.е. изучает движение материальных тел под действием приложенных к ним сил.
В основе классической (ньютоновской) механики лежат три закона динамики, сформулированные Ньютоном в 1687г.
Законы Ньютона (как и все остальные физические законы) возникли в результате обобщения большого количества опытных фактов. Правильность их (хотя и для очень обширного, но все же ограниченного круга явлений) подтверждается согласием с опытом тех следствий, которые из них вытекают.
Ньютоновская механика достигла в течение двух столетий таких огромных успехов, что многие физики 19в. были убеждены в ее всемогуществе. Считалось, что объяснить любое физическое явление означает свести его механическому процессу, подчиняющемуся законам Ньютона. Однако с развитием науки обнаружились новые факты, которые не укладывались в рамки классической механики. Эти факты получили свое объяснение в новых теориях – специальной теории относительности (СТО) и квантовой механике.
В СТО, созданной Эйнштейном в 1905г., подвергались радикальному пересмотру ньютоновские представления о пространстве и времени. Этот пересмотр привел к созданию релятивистской механики («механики больших скоростей»). Новая механика не привела, однако, к полному отрицанию старой ньютоновской механики. В пределе при скоростях малых по сравнению со скоростью света уравнения релятивистской механики переходят в уравнения классической механики.
Таким образом, классическая механика вошла в релятивистскую механику как ее частный случай и сохранила свое прежнее значение для описания движений, происходящих со скоростями значительно меньшими скорости света (v<<c).
Аналогично обстоит дело и с соотношением между классической и квантовой механикой, возникшей в 20х годах XXв. в результате развития физики атома. Уравнения квантовой механики также дают в пределе (для масс много больших по сравнению с массами атомов) уравнения классической механики. Следовательно, классическая механика вошла и в квантовую механику в качестве ее предельного случая.
Таким образом, развитие науки не перечеркнуло классическую механику, а лишь показало ее ограниченную применимость. Классическая механика, основываясь на законах Ньютона, является механикой тел больших (по сравнению с массой атомов) масс, движущихся с малыми (по сравнению со скоростью света) скоростями.
3.1. I закон Ньютона (закон инерции).
ОПРЕДЕЛЕНИЕ: Всякое тело находится (сохраняет) в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией.
Опыт показывает, что при одинаковом воздействии различные тела по-разному изменяют свою скорость. Иными словами, одинаковые воздействия вызывают у различных тел различные ускорения. Следовательно, величина ускорения, приобретаемого телом, зависит не только от величины воздействия, но и от некоторого собственного свойства тела. Это свойство тела характеризуют физической величиной, называемой массой.
ОПРЕДЕЛЕНИЕ: Масса тела – это физическая величина, характеризующая меру инерции тела.
Масса тела – это, прежде всего, его свойство откликаться определенным ускорением на действие определенного воздействия (силы).
Замечание: Различие понятий (терминов): «инерция» и «инертность».
Оба эти термина означают свойства тел, проявляющиеся в инерциальных системах отсчета. Но…
1. Свойство «инерции» заключается в том, что тела при отсутствии внешних воздействий сохраняют скорость своего движения неизменной (включая и случай 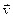 =0). Инерцией обладают любые тела, но для нее не вводится никакой количественной меры. Инерция – неизмеряемое свойство.
=0). Инерцией обладают любые тела, но для нее не вводится никакой количественной меры. Инерция – неизмеряемое свойство.
2. Свойство «инертности» состоит как раз в изменении скорости тел (в появлении ускорения) под действием внешних сил. Разные тела по-разному изменяют свои скорости под действием одной и той же силы, т.е. свойство инертности у них неодинаково. Инертность – свойство измеряемое. Масса и является мерой, количественной характеристикой этого свойства.
Первый закон Ньютона выполняется не во всякой системе отсчета. Как известно, характер движения зависит от выбора системы отсчета. Рассмотрим две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно, очевидно, будет двигаться с ускорением. Следовательно, I закон Ньютона не может одновременно выполняться в обеих системах.
ОПРЕДЕЛЕНИЕ: Система отсчета, в которой выполняется I закон Ньютона, называется инерциальной.
Сам закон называют иногда законом инерции. Система отсчета, в которой I закон Ньютона не выполняется, называется неинерциальной системой отсчета. Инерциальных систем отсчета существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы отсчета прямолинейно и равномерно ( 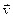 =const) будет также инерциальной.
=const) будет также инерциальной.
Опытным путем установлено, что гелиоцентрическая система отсчета (т.е. система отсчета, центр которой совмещен с Солнцем, а оси направлены на соответствующим образом выбранные звезды) является инерциальной. Строго говоря, система отсчета, связанная с Землей не является инерциальной, т.к. движется с ускорением относительно гелиоцентрической системы (Земля движется относительно Солнца по криволинейной траектории и совершает вращение вокруг своей оси). Однако ускорение такой системы настолько мало, что в большинстве случаев ее можно считать практически инерциальной.
Пример: 1. центростремительное ускорение суточного вращения экваториальных областей земной поверхности составляет около 0,03 м/с2.
2. центростремительное ускорение годового вращения Земли вокруг Солнца не превышает 0,001м/с2.
Анализ неинерциальных движений приводит к заключению, что внешней причиной неинерциального движения тел в инерциальной системе отсчета всегда является воздействие на него со стороны других объектов.
Для характеристики этого воздействия вводится понятие силы.
ОПРЕДЕЛЕНИЕ: Сила – физическая величина, характеризующая воздействие, оказываемое на тело со стороны других тел, в результате которого тело приобретает ускорение и являющаяся количественной мерой этого воздействия.
Сила – величина векторная и направлена так же, как вектор вызываемого этой силой ускорения.
В отличие от кинематики, где ускорение тела считается заданной величиной, в динамике устанавливается причинная и количественная связь ускорения с действующей на тело силой. Обобщение опытных фактов, позволяющих сделать это, составляет содержание II закона Ньютона.
II закон Ньютона.
ОПРЕДЕЛЕНИЕ: Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела: 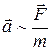 .
.
Этот закон, также как и I закон Ньютона справедлив только в инерциальных системах отсчета.
 В частном случае, при отсутствии воздействия на тело со стороны других тел (F = 0) ускорение a = 0, что совпадает с утверждением I закона Ньютона. Поэтому первый закон, казалось бы, входит во второй как его частный случай. Несмотря на это, I закон формулируется независимо от II закона, т.к. в нем, по сути, заключен постулат о существовании инерциальных систем отсчета.
В частном случае, при отсутствии воздействия на тело со стороны других тел (F = 0) ускорение a = 0, что совпадает с утверждением I закона Ньютона. Поэтому первый закон, казалось бы, входит во второй как его частный случай. Несмотря на это, I закон формулируется независимо от II закона, т.к. в нем, по сути, заключен постулат о существовании инерциальных систем отсчета.
Уточняя предыдущую формулу можно записать
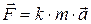 .
.
В данном случае единицу силы можно выбрать так, что k = 1, т.е.
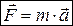 – основное уравнение классической механики
– основное уравнение классической механики
В соответствии с этой формулой за единицу силы следует принять силу, которая массе 1кг сообщает ускорение 1м/с2. Эта единица называется ньютон: 1Н=1кг×1 м/с2. Размерность силы: [F]= 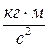 ; (1кГ=9,81Н).
; (1кГ=9,81Н).
II закон Ньютона можно записать в скалярной форме, взяв проекции силы на координатные оси X, Y и Z.
Важным положением динамики является принцип независимости действия сил. На практике на тело может действовать одновременно несколько сил: 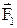 ,
, 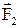 , …
, … 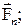 . И данный принцип гласит, что каждая из сил, действующих на тело, сообщает ему ускорение, подсчитываемое по основному уравнению механики, независимо от того действуют на него другие силы или нет, двигалось тело или покоилось. Согласно этому можно записать:
. И данный принцип гласит, что каждая из сил, действующих на тело, сообщает ему ускорение, подсчитываемое по основному уравнению механики, независимо от того действуют на него другие силы или нет, двигалось тело или покоилось. Согласно этому можно записать:
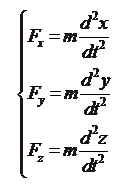
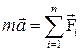 , где
, где 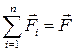 – результирующая сила.
– результирующая сила.
II закон Ньютона можно записать и в другом виде.
Пусть на тело массой «m» в течение некоторого промежутка времени Dt, двигавшееся со скоростью 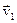 подействовала постоянная сила
подействовала постоянная сила 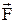 . Она будет сообщать телу постоянное ускорение
. Она будет сообщать телу постоянное ускорение 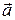 , в связи, с чем к концу промежутка времени тело приобретет скорость
, в связи, с чем к концу промежутка времени тело приобретет скорость 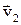 . Тогда, согласно второму закону Ньютона можно записать
. Тогда, согласно второму закону Ньютона можно записать
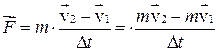 .
.
Величину 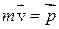 называют импульсом тела (старое название «количество движения»). Направление вектора
называют импульсом тела (старое название «количество движения»). Направление вектора 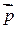 совпадает с направлением вектора
совпадает с направлением вектора 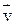 . Имеем
. Имеем 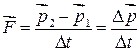 , где
, где 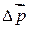 – изменение вектора импульса тела.
– изменение вектора импульса тела.
ОПРЕДЕЛЕНИЕ: Изменение вектора импульса тела со временем равно результирующей всех сил, действующих на тело (закон изменения импульса тела).
Если сила 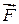 переменна, то при Dt®0 получаем
переменна, то при Dt®0 получаем 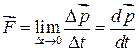 – это более общее выражение II закона Ньютона, верное и для больших скоростей, когда масса начинает быстро расти по закону
– это более общее выражение II закона Ньютона, верное и для больших скоростей, когда масса начинает быстро расти по закону 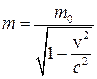 .
.
Добавим, что величину 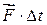 называют импульсом силы.
называют импульсом силы.
Тогда, если силу, действующую на тело в течение малого промежутка времени можно практически считать постоянной, то закон изменения импульса можно записать в виде:
ОПРЕДЕЛЕНИЕ: Импульс силы, действующей на тело в течение малого промежутка времени, равен изменению импульса тела (или изменению количества движения).
Замечание: Основной закон динамики (II закон Ньютона) используется для решения основной задачи динамики, которая кратко формулируется так: требуется определить закон движения материальной точки, если известны действующие на нее силы. Логика решения такова: определив ускорение, с помощью известных формул кинематики ищутся выражения для скоростей и координат.
III закон Ньютона.
Всякое действие тел друг на друга носит характер взаимодействия: если тело M1 действует на тело M2 с некоторой силой f12, то и тело M2 в свою очередь действует на тело M1 с силой f21.
Как показывает опыт, силы, с которыми действуют друг на друга взаимодействующие тела, оказываются всегда равными по величине и противоположными по направлению.
 Рассмотрим пример:
Рассмотрим пример:
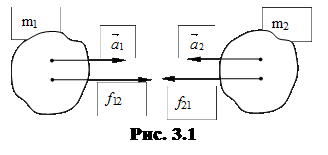
Два тела с массами m1 и m2, изолированные от действия внешних сил притягиваются (или отталкиваются) друг от друга вследствие того, что, например, несут электрические заряды. Под действием сил 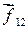 и
и 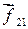 тела приобретают ускорения
тела приобретают ускорения 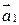 и
и 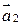 соответственно (рис. 3.1). Величина этих ускорений оказывается обратной массам тел:
соответственно (рис. 3.1). Величина этих ускорений оказывается обратной массам тел: 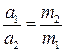 . Откуда следует равенство
. Откуда следует равенство 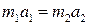 и равенство сил f12=f21. Направления этих сил, очевидно, противоположны.
и равенство сил f12=f21. Направления этих сил, очевидно, противоположны.
К этому же результату можно прийти, сопоставляя не ускорения тел, а растяжения калиброванных пружин.
Третий закон Ньютона как раз и является обобщением опытных фактов подобного рода.
Современная формулировка третьего закона Ньютона выглядит следующим образом:
ОПРЕДЕЛЕНИЕ: Всякое действие тел друг на друга носит характер взаимодействия, силы с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.
Математически содержание III закона Ньютона можно записать в следующем виде:
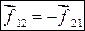 (3.1)
(3.1)
Эти силы, очевидно, приложены к различным телам. Пусть под действием силы 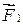 тело приобретает ускорение
тело приобретает ускорение 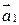 , а под действием силы
, а под действием силы 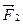 – ускорение
– ускорение 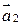 , тогда
, тогда 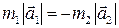 и, следовательно,
и, следовательно, 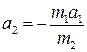 , т.е. ускорения, полученные телами в результате их взаимодействия, обратно пропорциональны массам тел и имеют противоположные направления.
, т.е. ускорения, полученные телами в результате их взаимодействия, обратно пропорциональны массам тел и имеют противоположные направления.
Теперь рассмотрим изолированную систему.
ОПРЕДЕЛЕНИЕ: Изолированной системой называется система тел, которые взаимодействуют друг с другом и не взаимодействуют ни с какими иными телами.
или
Изолированной системой называется система, в которой действуют только внутренние силы, и где не учитывается влияние внешних сил.

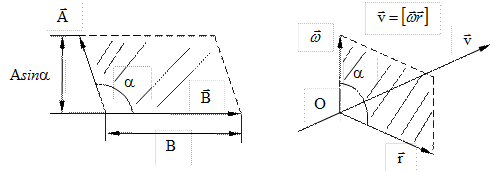 Рис. 2.20
Рис. 2.20