Моменты инерции некоторых тел правильной геометрической формы

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции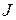
Однородный тонкий стержень массой т и длиной l	Проходит через центр тяжести стержня перпендикулярно стержню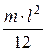
Проходит через конец стержня перпендикулярно стержню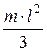
Тонкое кольцо, обруч, труба радиусом R и массой т, маховик радиусом R и массой т,распределённой по ободу	Проходит через центр перпендикулярно плоскости основания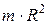
Круглый однородный диск (цилиндр) радиусом R и массой т	Проходит через центр диска перпендикулярно плоскости основания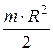
Толстостенная трубка, круглый однородный полый диск (цилиндр) массой т с внутренним радиусом R1 и внешним радиусом R2	Проходит через центр диска перпендикулярно плоскости основания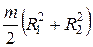
Однородный шар массой т и радиусом R	Проходит через центр шара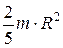

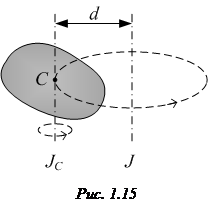
· Теорема Штейнера: момент инерции тела относительно произвольной оси равен:

,

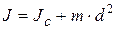где 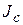– момент инерции этого тела относительно оси, проходящей через центр масс тела параллельно заданной оси; 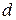– расстояние между осями; m – масса тела (рис. 1.15).

· Момент импульса вращающегося тела относительно оси:

,

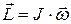где 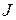– момент инерции тела, 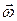– его угловая скорость.

· Закон сохранения момента импульса. Если суммарный момент внешних сил, действующих на систему, равен нулю, то полный момент импульса системы сохраняется:

Если 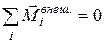, то ,

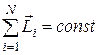или ,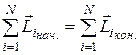

где L_i – момент импульса i-го тела, входящего в состав системы, N – число тел в системе. Для двух взаимодействующих тел замкнутой системы:

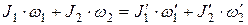
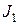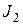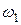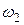где , , и – моменты инерции и угловые скорости тел до взаимодействия: 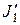, , 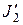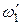и 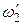– те же величины после взаимодействия.

· Закон сохранения момента импульса для одного тела, момент инерции которого меняется:

,

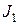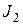где и – начальный и конечный моменты инерци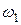и; и 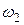– начальная и конечная угловые скорости тела.

· Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси (второй закон Ньютона для вращательного движения): угловое ускорение 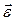тела прямо пропорционально суммарному моменту 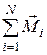внешних сил и обратно пропорционально моменту инерции 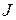тела:

.

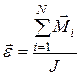· Второй закон Ньютона для вращательного движения в импульсной форме (закон изменения момента импульса тела): изменение момента импульса тела 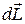равно импульсу 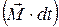суммарного момента 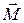внешних сил:

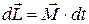, или .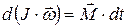

Если момент сил, действующих на тело, постоянен, то

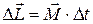, или ,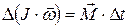

где 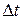(или 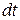) – промежуток времени, в течение которого действовал момент сил 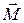; 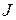– момент инерции тела, 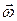– его угловая скорость.

· Работа момента силы 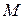при вращательном движении:

, .

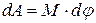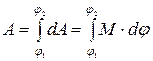Если момент сил постоянен ( 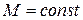), то работа равна

.

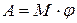Здесь 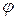(или 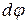) – угол поворота.

· Мгновенная мощность, развиваемая при вращении тела:

.

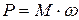· Кинетическая энергия вращающегося тела:

.

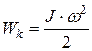· Кинетическая энергия тела, катящегося по плоскости без скольжения:

,

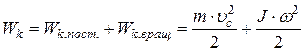где 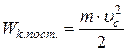– кинетическая энергия поступательного движения тела; 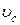– скорость центра масс тела; 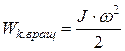– кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр масс.

Механические колебания

· Кинематическое уравнение гармонических колебаний

,

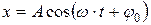Здесь х –смещение колеблющейся точки из положения равновесия;

t – время;

А –амплитуда колебаний;

ω – круговая (циклическая) частота колебаний;

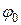– начальная фаза колебаний;

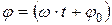– фаза колебаний в момент t.

· Круговая (циклическая) частота колебаний:

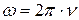, или ,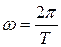

где 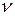и Т – частота (линейная частота) и период колебаний соответственно.

· Скорость точки, совершающей гармонические колебания:

.

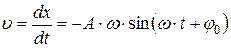· Ускорение колеблющейся точки при гармонических колебаниях:

.

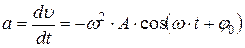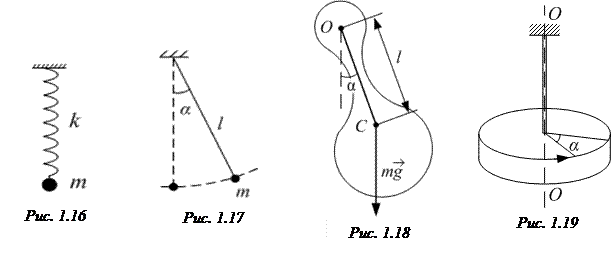
· Период колебаний пружинного маятника (тела массой m, подвешенного на пружине жёсткостью k, рис. 1.16):

.

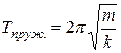Формула справедлива для малых колебаний, пока выполняется закон Гука 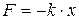, и в пренебрежении массой пружины в сравнении с массой тела.

· Период колебаний математического маятника (материальной точки массой m, подвешенной на нерастяжимой невесомой нити длиной l, рис. 1.17):

,

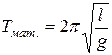где g –ускорение свободного падения.

· Период колебаний физического маятника (твёрдого тела, подвешенного в поле силы тяжести и способного колебаться относительно оси, не проходящей через центр масс, рис. 1.18):

.

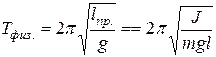Здесь J – момент инерции колеблющегося тела относительно оси колебаний, l – расстояние от центра масс маятника до оси (длина физического маятника), 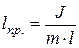– приведённая длина физического маятника (то есть длина такого математического маятника, который имеет тот же период колебаний).

Формулы для периода колебаний физического и математического маятников справедливы при малых углах отклонения, когда можно положить 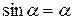. Для α=15⁰ ошибка в значении периода не превышает 1 %, а при α=3⁰ ошибка равна 0.005 %.

· Период колебаний крутильного маятника (тела, подвешенного на упругой нити, рис. 1.19):

,

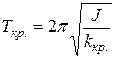где J –момент инерции тела относительно оси, совпадающей с нитью, 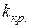– модуль кручения нити. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука: 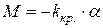. Здесь M – момент упругой силы, возникающей при закручивании нити на угол .

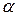· Полнаяэнергия гармонического осциллятора:

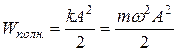
· Закон сохранения энергии при гармонических колебаниях:

.

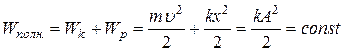· Амплитуда Арезультирующего колебания 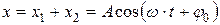, полученного при сложении двух колебаний одинаковой частоты, происходящих по одной прямо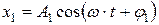й,

и

,

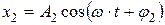равна

,

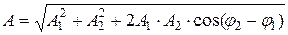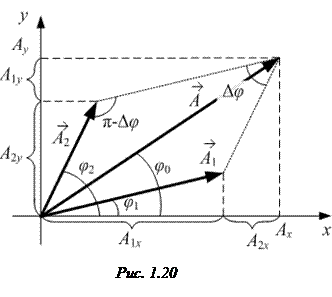где А₁и А₂ – амплитуды исходных колебани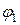й; и 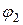– их начальные фазы (см. сложение колебаний по методу векторных диаграмм на рис. 1.20).

· Начальная фаза результирующего колебания при сложении однонаправленных колебаний:

.

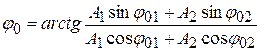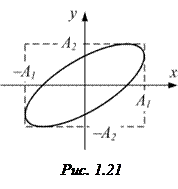· Уравнение траектории (рис. 1.21) точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты,

и ,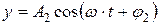

с амплитудами А₁и А₂ и начальными фазам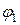и и :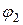

,

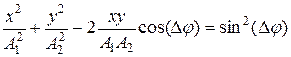где 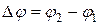– сдвиг фаз колебаний.

· Возвращающая (квазиупругая) сила, действующая на тело массой m при гармонических колебаниях:

,

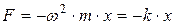где х –смещение колеблющейся точки из положения равновесия; ω – циклическая частота колебаний; 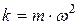– коэффициент пропорциональности. В частном случае пружинного маятника он равен жёсткости пружины.

· Дифференциальное уравнение гармонических колебаний

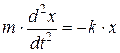, или в стандартной форме:

,

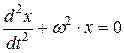где x – колеблющаяся величина; ω – круговая (циклическая) частота колебаний; 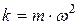– коэффициент квазиупругой силы.

· Дифференциальное уравнение затухающих колебаний

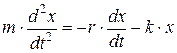, или в стандартной форме:

,

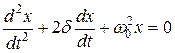где r – коэффициент сопротивления (коэффициент пропорциональности между силой сопротивления и скоростью: 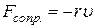); 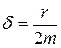– коэффициент затухания; 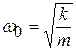– круговая частота собственных (незатухающих) колебаний.

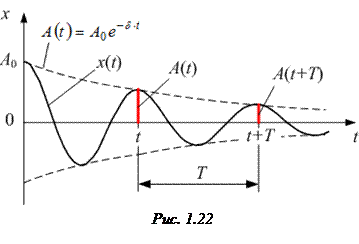
· Кинематическое уравнение затухающих колебаний (рис.1.22):

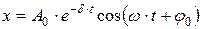, или .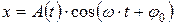

Здесь 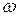– круговая частота затухающих колебаний:

.

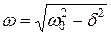· Амплитуда затухающих колебаний:

,

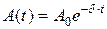где А₀–амплитуда колебаний в момент t=0.

· Логарифмический декремент затухания равен по определению логарифму отношения амплитуд 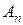и 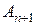двух следующих друг за другом колебаний, то есть колебаний, отстоящих во времени друг от друга на один период (рис. 1.22):

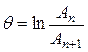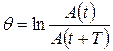, или , или .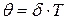

· Добротность

.

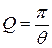При условии 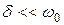(затухание мало):

.

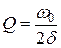Если 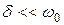, то добротность обратно пропорциональна относительному изменению энергии 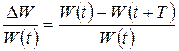за один период:

.

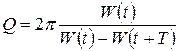· Дифференциальное уравнение вынужденных колебаний:

,

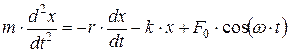или в стандартной форме:

.

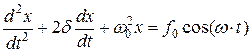Здесь 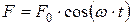– вынуждающая сила (внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания); 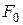– её амплитудное значение; ω – её циклическая частота; 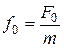; 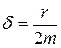– коэффициент затухания; 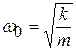– циклическая частота собственных (незатухающих) колебаний.

· Кинематическое уравнение вынужденных колебаний:

.

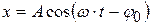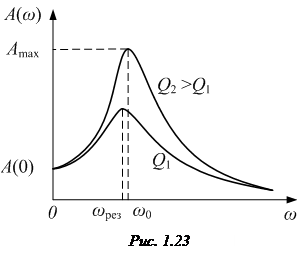· Амплитуда вынужденных колебаний как функция частоты (рис. 1.23):

.

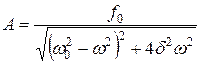· Начальная фаза вынужденных колебаний:

.

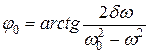· Резонансная частота:

.

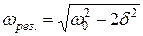· Максимальная амплитуда (амплитуда при резонансе):

.

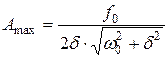Волны

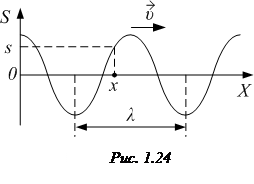· Уравнение плоской волны, бегущей в положительном направлении оси OX (рис. 1.24):

,

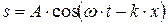где s – смещение частиц с координатой x из положения равновесия в момент времени t,

A – амплитуда,

ω – циклическая частота,

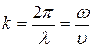– волновое число (модуль волнового вектора),

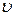– фазовая скорость (скорость распространения фиксированной фазы волны ),

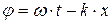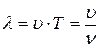– длина волны (расстояние, на которое распространяется волна за время, равное периоду колебаний),

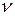– частота колебаний.

· Уравнениесферической волны:

,

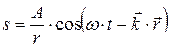Здесь s – смещение частиц с радиус-вектором 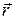из положения равновесия в момент времени t;

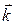– волновой вектор, равный по величине 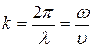, направленный вдоль луча;

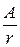– амплитуда сферической волны; r – расстояние до источника.

· Скорость распространения продольных и поперечных упругих волн в твёрдом теле:

, ,

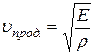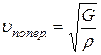где E – модуль Юнга, G – модуль сдвига, ρ – плотность.

· Скорость звука в газе:

,

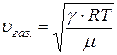где Т – абсолютная температура, R – универсальная газовая постоянная, μ – молярная масса газа, γ – показатель Пуассона (для воздуха ).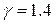

· Скорость распространения поперечной волны по струне:

,

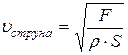где F – сила натяжения струны, S – площадь сечения струны, ρ – плотность.

Задачи к разделу 1

1. Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 60⁰ к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1,7 с.

2. Две частицы движутся с ускорением g в однородном поле силы тяжести. В начальный момент частицы находились в одной точке и имели скорости 3 м/с и 4 м/с, направленные горизонтально в противоположные стороны. Найти расстояние между частицами в момент, когда векторы их скоростей окажутся взаимно перпендикулярными.

3. Кабина лифта, у которой расстояние от пола до потолка равно 2,7 м, начала подниматься с постоянным ускорением 1,2 м/с². Через 2 с после начала подъема с потолка кабины стал падать болт. Найти: а) время свободного падения болта; б) перемещение и путь болта за время свободного падения в системе отсчёта, связанной с шахтой лифта.

4. В момент времени t=0 частица вышла из начала координат в направлении, противоположном оси x. Её скорость меняется по закону 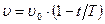, где 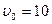см/с – модуль начальной скорости; Т=5 с. Найти: а) координату х частицы в моменты времени 6 с, 10 с и 20 с; б) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат; в) путь S, пройденный частицей за первые 4 с и 8 с; г) изобразить примерный график S(t).

5. Материальная точка движется прямолинейно с ускорением а=5 м/с². Определить, насколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять .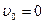

6. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью 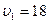км/ч. Далее половину оставшегося времени он ехал со скоростью 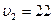км/ч, после чего до конечного пункта он шел пешком со скоростью 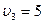км/ч. Определить среднюю скорость велосипедиста.

7. Тело брошено с начальной скоростью с высоты h=2,4 м вверх под углом 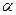=35⁰ к горизонту и упало на расстоянии l=37 м от места бросания. Найти начальную скорость тела.

8. Тело брошено с вышки в горизонтальном направлении со скоростью 20 м/с. Определить скорость тела и её направление в конце второй секунды после начала движения.

9. Твердое тело вращается вокруг неподвижной оси по закону 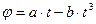, где а=6 рад/с, b=2 рад/с³. Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от начала вращения до остановки; б) угловое ускорение в момент остановки тела.

10. Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением. Определить тангенциальное ускорение 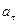точки, если известно, что за время 4 с она совершила три оборота и в конце третьего оборота её нормальное ускорение 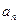=2,7 м/с².

11. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m₁=5,1 кг и m₂=2,2 кг на концах. Груз m₁ скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m₂. Угол наклонной плоскости с горизонтом 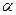=37⁰, коэффициент трения между грузом m₁ и плоскостью равен 0,1. Определить ускорение грузов.

12. На верхнем конце наклонной плоскости укреплен легкий блок, через который перекинута нить с грузами m₁=1,7 кг и m₂=0,4 кг на концах. Груз m₁ скользит вниз по наклонной плоскости, поднимая висящий на другом конце нити груз m₂. Угол наклонной плоскости с горизонтом 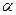=48⁰, ускорение грузов а=2,1 м/с². Определить коэффициент трения между грузом m₁ и плоскостью.

13. На разных склонах наклонной плоскости, образующих с горизонтом углы 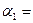32⁰ и 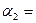48⁰, находятся грузы m₁=3,3 кг и m₂. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,1, ускорение грузов а= –1,2 м/с² (а > 0, если система движется в сторону груза m₂). Определить массу второго груза m₂.

14. На разных склонах наклонной плоскости, образующих с горизонтом углы 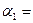65⁰и 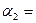35⁰, находятся грузы m₁=1,8 кг и m₂=5,6 кг. Нить, связывающая грузы, перекинута через легкий блок, укрепленный на вершине наклонной плоскости. Коэффициент трения между грузами и наклонной плоскостью равен 0,12, ускорение грузов а (а > 0, если система движется в сторону груза m₂). Определить ускорение грузов а.

15. Шарик массой m=45 г падает на горизонтальную поверхность стола с высоты h₁=2,4 м и, отскочив, поднимается на некоторую высоту h₂. Время соударения t=0,49 мс, средняя сила взаимодействия шарика со столом F=1200 Н. Найти h₂.

16. Через блок перекинута нить, к концам которой подвешены гири массами m₁=m₂=1 кг. Какую силу нужно приложить к одной из гирь, чтобы гири стали двигаться с ускорением а=3 м/с²? Массой блока пренебречь.

17. Автомобиль массой m=5000 кг движется со скоростью 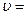10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней точке, если радиус кривизны моста R=50 м.

18. Какую наибольшую скорость может развивать велосипедист, проезжая закругление R=50 м, если коэффициент трения скольжения между шинами и асфальтом равен 0,3? Каков угол отклонения 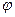велосипеда от вертикали, когда велосипедист движется по закруглению?

19. Тело, двигаясь равноускоренно, соскользнуло с наклонной плоскости длиной l=2 м за время t=2 c. Определить коэффициент трения тела о плоскость. Угол наклона 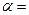30⁰.

20. Тело массой 0.2 кг движется прямолинейно, причем координата изменяется по закону x=A–Bt+5t²–t³ (время – в секундах, координата – в метрах). Найти силу, действующую на тело в конце второй секунды движения.

21. Две лодки массами m₁=250 кг и m₂=370 кг идут параллельными курсами со скоростями 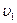=1,6 м/с и 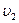. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=32 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u₁ и u₂=2,1 м/с. Найти скорость u₁.

22. Две лодки массами m₁=310 кг и m₂=160 кг идут параллельными курсами со скоростям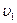и и 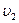. Когда лодки оказываются рядом, из каждой лодки в другую перекладывается мешок массой m=25 кг, после чего лодки продолжают двигаться параллельными курсами, но со скоростями u₁= -1,7 м/с и u₂=2,8 м/с. Найти скорость .

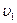23. Снаряд, летящий со скоростью 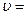750 м/с, разрывается на два осколка массами m₁=45 кг и m₂=17 кг, разлетающихся под углом 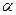со скоростями u₁=710 м/с и u₂=900 м/с. Определить угол .

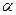24. Снаряд, летящий со скоростью 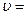550 м/с, разрывается на два осколка массами m₁=14 кг и m₂=8 кг, разлетающиеся под углом 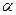=95⁰ со скоростями u₁ и u₂=830 м/с. Определить скорость u₁.

25. Человек массой m₁=55 кг, стоящий на одном конце первоначально покоящейся тележки массой m₂=120 кг и длиной l=4,5 м, прыгает со скоростью 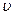относительно земли под углом 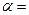25⁰ к горизонту и попадает на другой конец тележки. Массу колёс, а также силу сопротивления движению тележки не учитывать. Определить скорость .

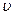26. Человек массой m₁=45 кг, стоящий на одном конце первоначально покоящейся тележки массой m₂=160 кг и длиной l=3,5 м, прыгает со скоростью 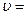5,5 м/с относительно земли под углом 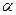к горизонту и попадает на другой конец тележки. Массу колес, а также силу сопротивления движению тележки не учитывать. Определить угол .

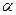27. В деревянный шар массой m₁=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля m₂=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в ней пулей отклонилась от вертикали на угол 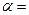3⁰? Размером шара пренебречь. Удар пули считать прямым, центральным.

28. Шар массой m₁=5 кг движется со скоростью 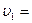1 м/с и сталкивается с покоящимся шаром массой m₂=2 кг. Определить скорости шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

29. Шар массой m₁=2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m₂ большего шара. Удар считать абсолютно упругим, прямым, центральным.

30. Два груза массами m₁=10 кг и m₂=15 кг подвешены на нитях длиной l=2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол 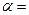60⁰ и отпущен. На какую высоту поднимутся оба груза после удара? Удар считать неупругим.

31. Шайба массой m=50 г соскальзывает без начальной скорости по наклонной плоскости, составляющий угол 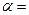30⁰ с горизонтом, и, пройдя по горизонтальной плоскости расстояние l=50 см, останавливается. Найти работу сил трения на всем пути, считая всюду коэффициент трения равным 0,15.

32. Из пружинного пистолета с жёсткостью пружины k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость пули при выстреле её из пистолета, если пружина была сжата на 4 см.

33. Молот массой m₁=5 кг ударяет о небольшой кусок железа, лежащий на наковальне. Масса наковальни m₂=100 кг. Массой куска железа пренебречь. Удар неупругий. Определить КПД удара молота при данных условиях.

34. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то она сожмется на 3 мм. Насколько сожмет пружину тот же груз, упавший на конец пружины с высоты 8 см?

35. Определить работу растяжения двух последовательно соединённых пружин жесткостями k₁=0,5 кН/м и k₂=1 кН/м, если первая пружина при этом растянулась на 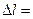2 см.

36. Две пружины жесткостями k₁=400 Н/м и k₂=250 Н/м соединены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации 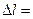4 см.

37. Из шахты глубиной h=600 м поднимают клеть массой m=3 т на канате, каждый метр которого имеет массу m₁=1,5 кг. Какая работа совершается при поднятии клети на поверхность Земли? Каков КПД подъемного устройства?

38. Налетев на пружинный буфер, вагон массой m=16 т, двигавшийся со скоростью 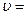0,6 м/с, остановился, сжав пружину на 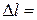8 см. Найти общую жесткость пружин буфера.

39. Цепь длиной l=2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает 1/3 длины цепи, то цепь соскальзывает со стола. Определить скорость цепи в момент её отрыва от стола.

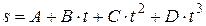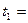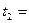40. Материальная точка массой m=2 кг двигалась под действием некоторой силы согласно уравнению , где А=10 м, В= –2 м/с, С=1 м/с², D= –0,2 м/с³. Найти мощность, развиваемую при движении, в моменты времени 2 c и 5 c.

41. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы и, обойдя её, вернётся в исходную точку? Масса платформы m₁=240 кг, масса человека m₂=60 кг. Момент инерции человека рассчитывать как для материальной точки.

42. Маховик, вращающийся с постоянной угловой скоростью 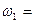62,8 рад/с, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова сделалось равномерным, но уже с угловой скоростью 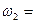37,7 рад/с. Определить угловое ускорение маховика и продолжительность торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.

43. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается по инерции около вертикальной оси с частотой 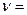10 об/мин. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

44. По касательной к шкиву маховика в виде диска диаметром D=75 см и массой m=40 кг приложена сила F=10 Н. Определить угловое ускорение и частоту вращения маховика через 10 с после начала действия силы, если радиус шкива R= 12 см. Силой трения пренебречь.

45. Нить с привязанными к её концам грузами массой m₁=50 г и m₂=60 г перекинута через блок диаметром D=4 см. Определить момент инерции блока, если под действием силы тяжести грузов он получил угловое ускорение 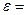1,5 рад/с².

46. Маховик в виде диска массой m=50 кг и радиусом R=20 см был раскручен до угловой скорости 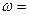50 рад/с и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент сил трения, считая его постоянным, принимая во внимание, что: а) маховик остановился через 50 с; б) маховик остановился, сделав 200 оборотов.

47. На краю платформы в виде диска диаметром D=2 м, вращающейся по инерции вокруг вертикальной оси с частотой 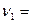0,13 Гц, стоит человек массой m=70 кг. Когда человек перешёл в центр платформы, она стала вращаться с частотой 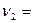0,16 Гц. Определить массу платформы.

48. Платформа в виде диска диаметром D=3 м и массой m₁=180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться платформа, если по её краю пойдет человек массой m₂=70 кг со скоростью 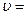1,8 м/с относительно платформы?

49. Блок, имеющий форму диска массой m=0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m₁=0,3 кг и m₂=0,7 кг. Определить силы натяжения нити по обе стороны блока.

50. Человек массой m₂=60 кг стоит на краю неподвижной платформы в виде диска диаметром D=0.8 м и массой m₁=20 кг. С какой угловой скоростью начнёт вращаться платформа, если человек поймает мяч массой m₃=1 кг, летящий со скоростью 10 м/с по касательной к краю платформы?

51. Маховик в виде сплошного диска радиусом R=20 см и массой m=50 кг раскручен до частоты вращения 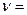8 Гц и предоставлен самому себе. Под действием силы трения маховик остановился через 50 с. Найти момент сил трения.

52. Маховик, массу которого m=5 кг можно считать распределенной по ободу радиусом R=20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 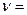12 Гц. При торможении маховик останавливается через 20 с. Найти тормозящий момент и число оборотов, которые сделает маховик до полной остановки.

53. Вал в виде сплошного цилиндра массой m₁=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m₂=2 кг. С каким ускорением будет опускаться гиря, если её предоставить самой себе?

54. Сплошной цилиндр массой m=4 кг катится без скольжения по горизонтальной поверхности. Линейная скорость оси цилиндра 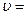1 м/с. Определить полную кинетическую энергию цилиндра.

55. Обруч и сплошной цилиндр, имеющие одинаковую массу m=2 кг, катятся без скольжения с одинаковой скоростью