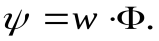Циркуляция вектора магнитной индукции. Закон полного тока.
По определению циркуляция вектора 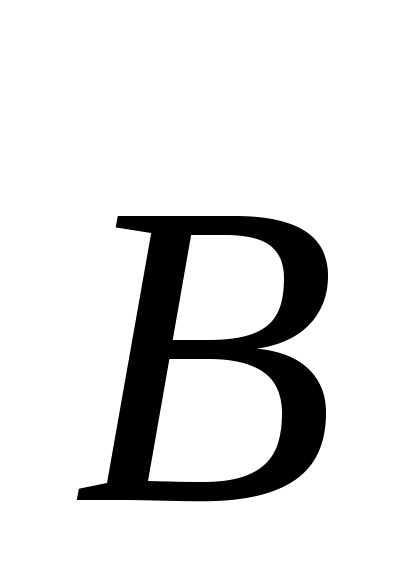 равна интегралу
равна интегралу 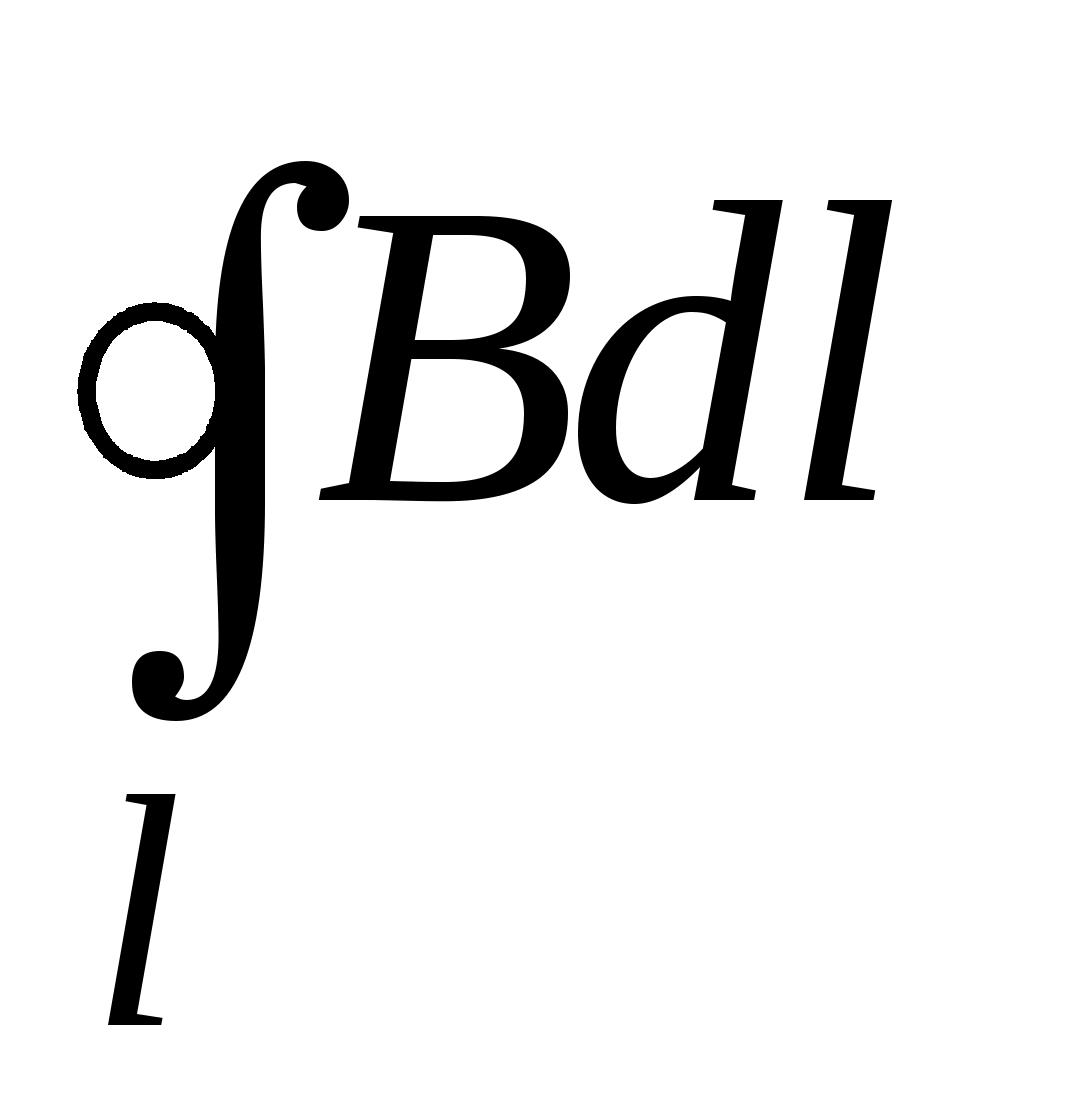 . Вычислим этот интеграл в случае прямого тока.
. Вычислим этот интеграл в случае прямого тока.
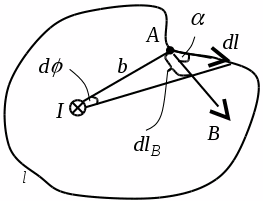 | Пусть замкнутый контур 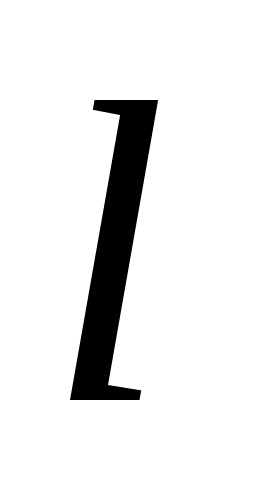 лежит в плоскости, перпендикулярной к току (рис. 23.8). В каждой точке контура вектор лежит в плоскости, перпендикулярной к току (рис. 23.8). В каждой точке контура вектор 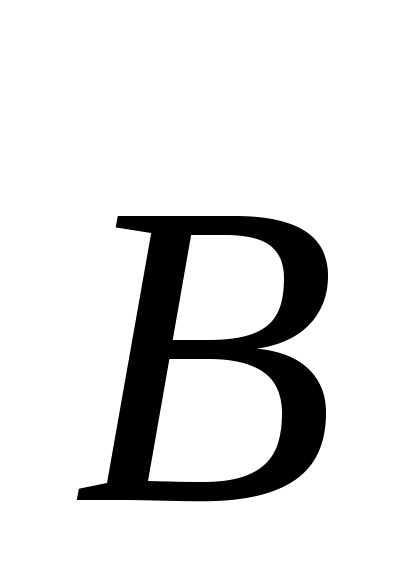 направлен по касательной к окружности, проходящей через точку А. Расстояние от тока направлен по касательной к окружности, проходящей через точку А. Расстояние от тока 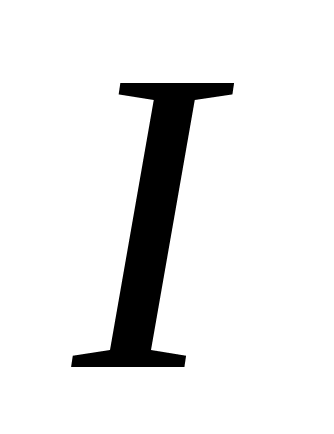 до т. А обозначим до т. А обозначим 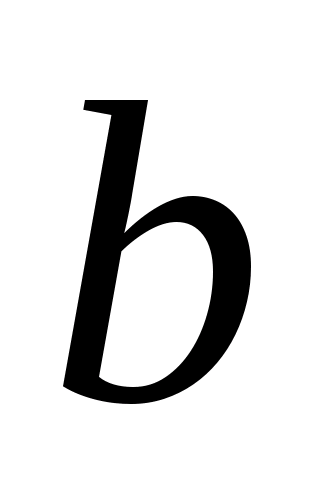 . Скалярное произведение . Скалярное произведение 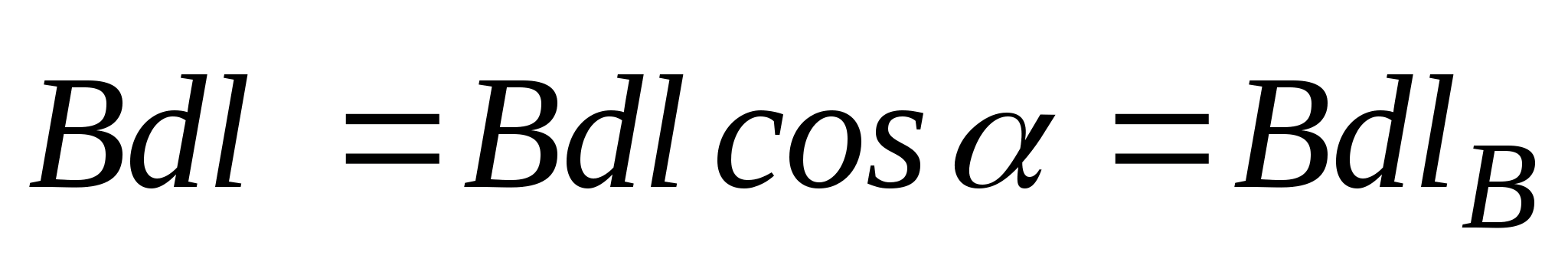 , где , где 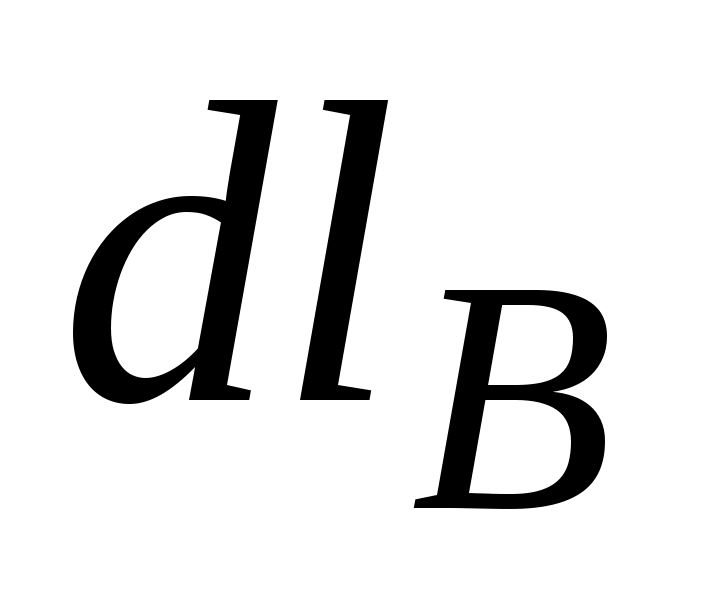 – проекция – проекция 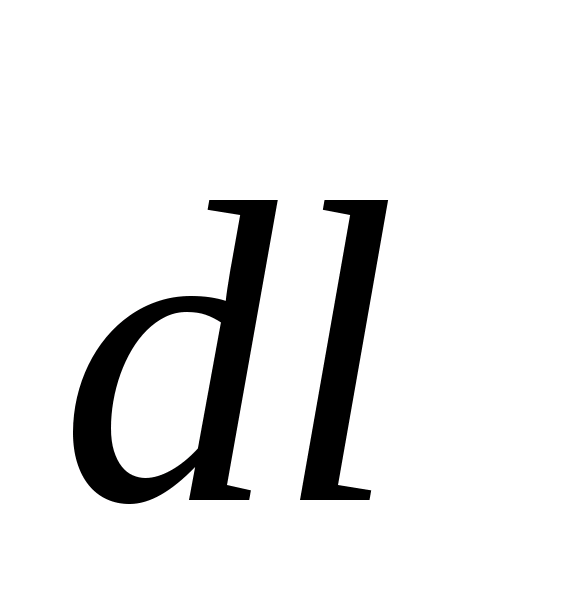 на направление вектора на направление вектора 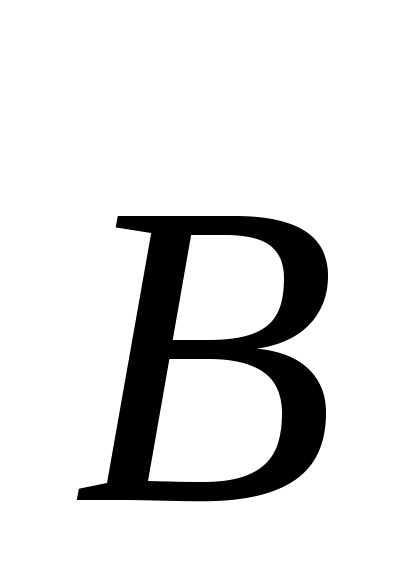 . В силу малости угла . В силу малости угла 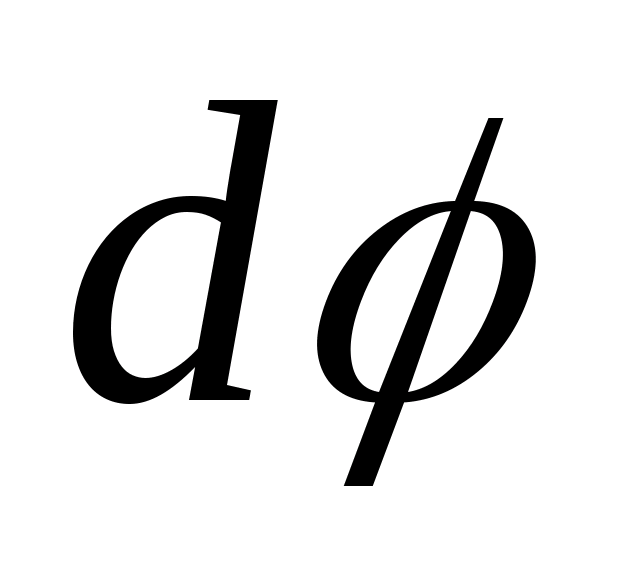 , , 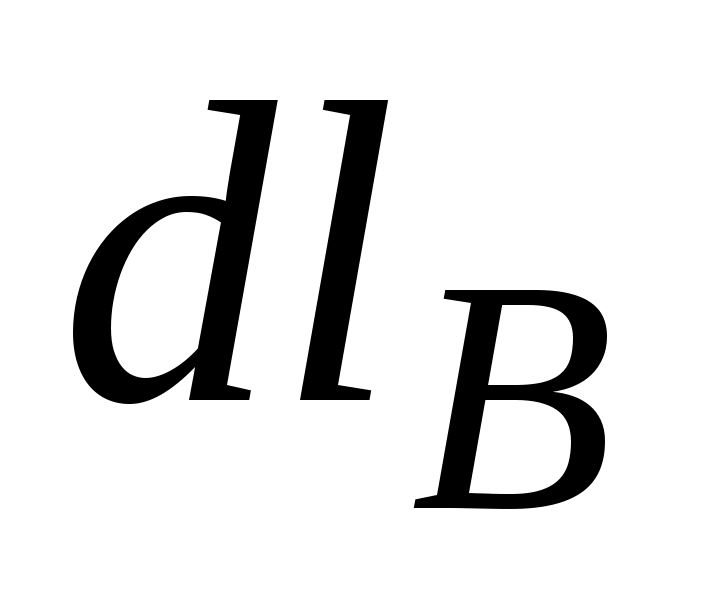 можно найти как длину дуги можно найти как длину дуги 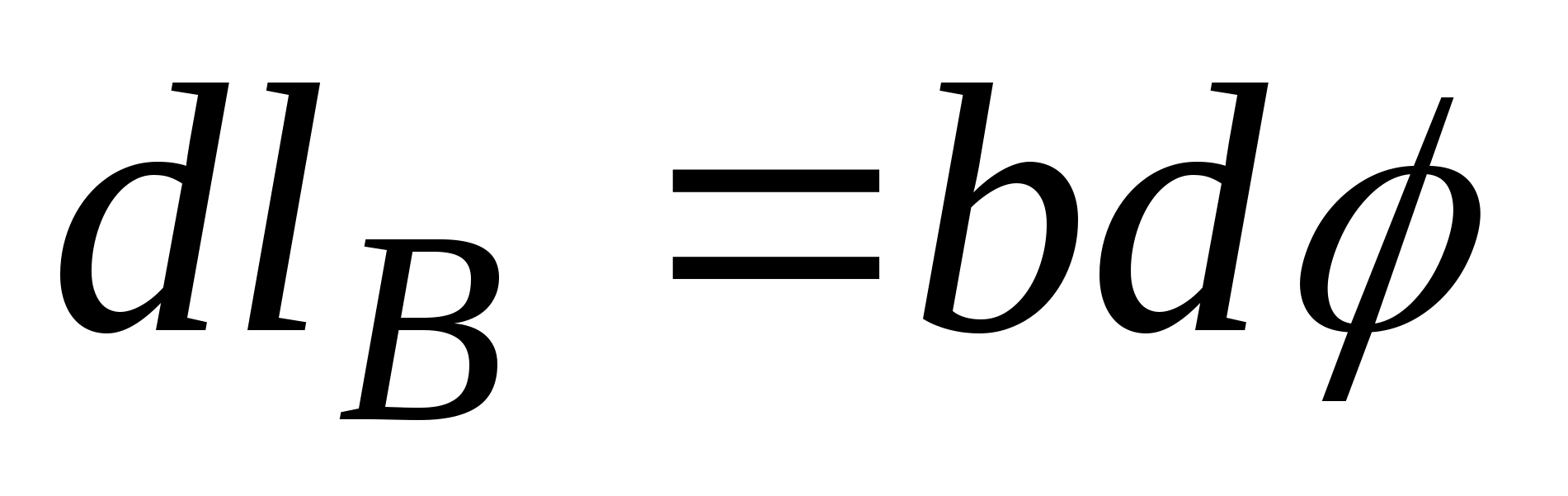 . . |
| Рис. 23.8 |
Магнитная индукция, создаваемая бесконечным прямолинейным током 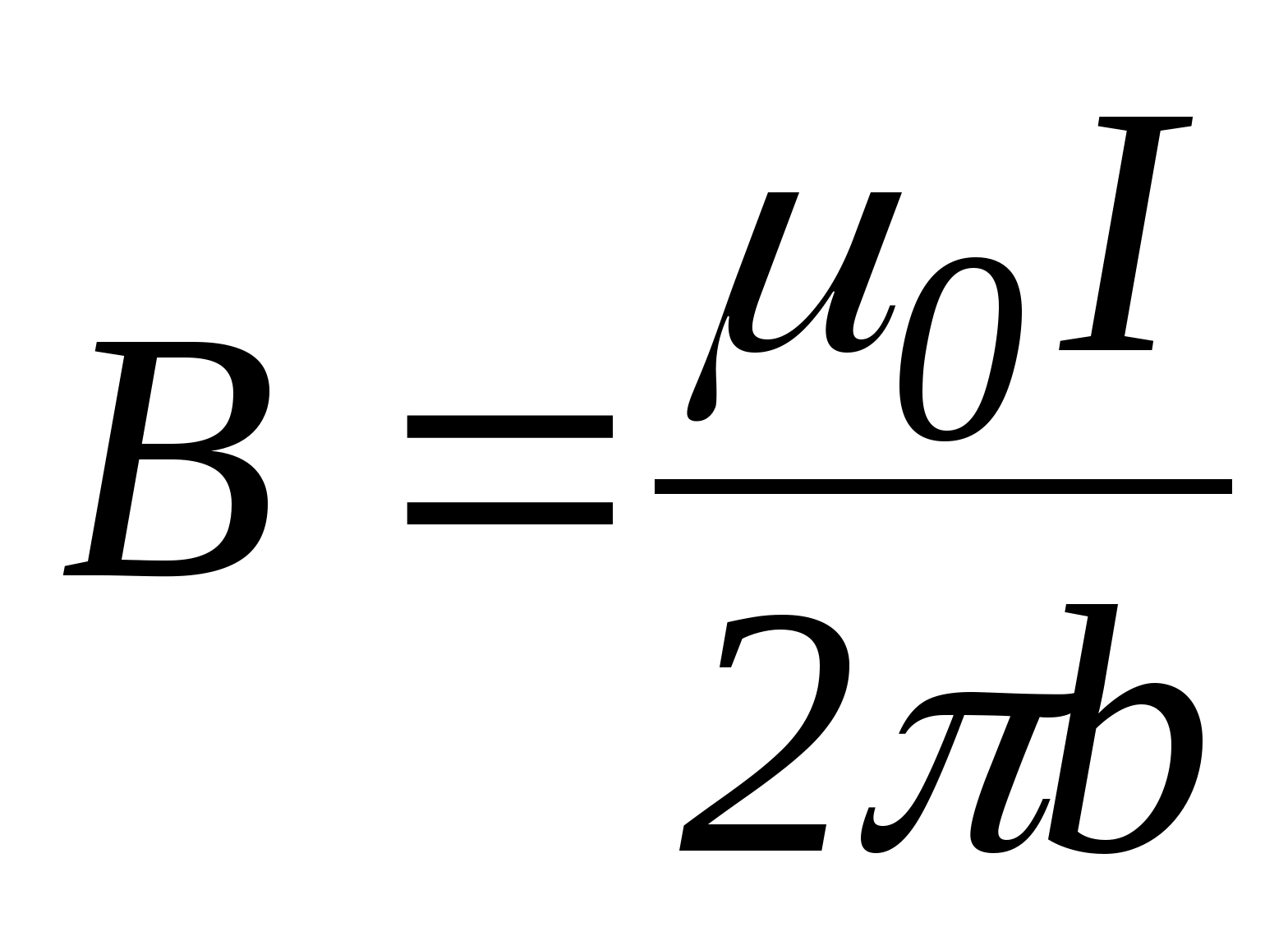 . Тогда
. Тогда 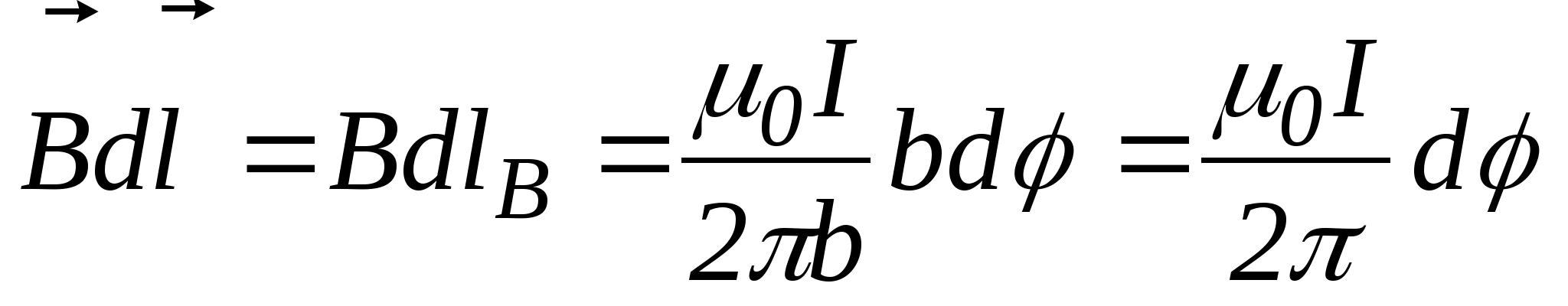 .
.
Интегрируя по контуру 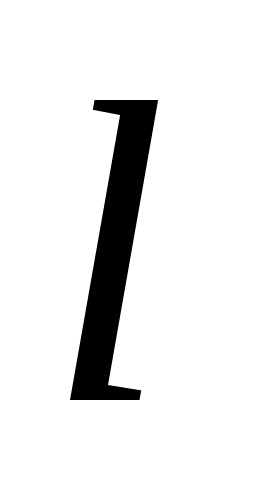 , получим:
, получим:
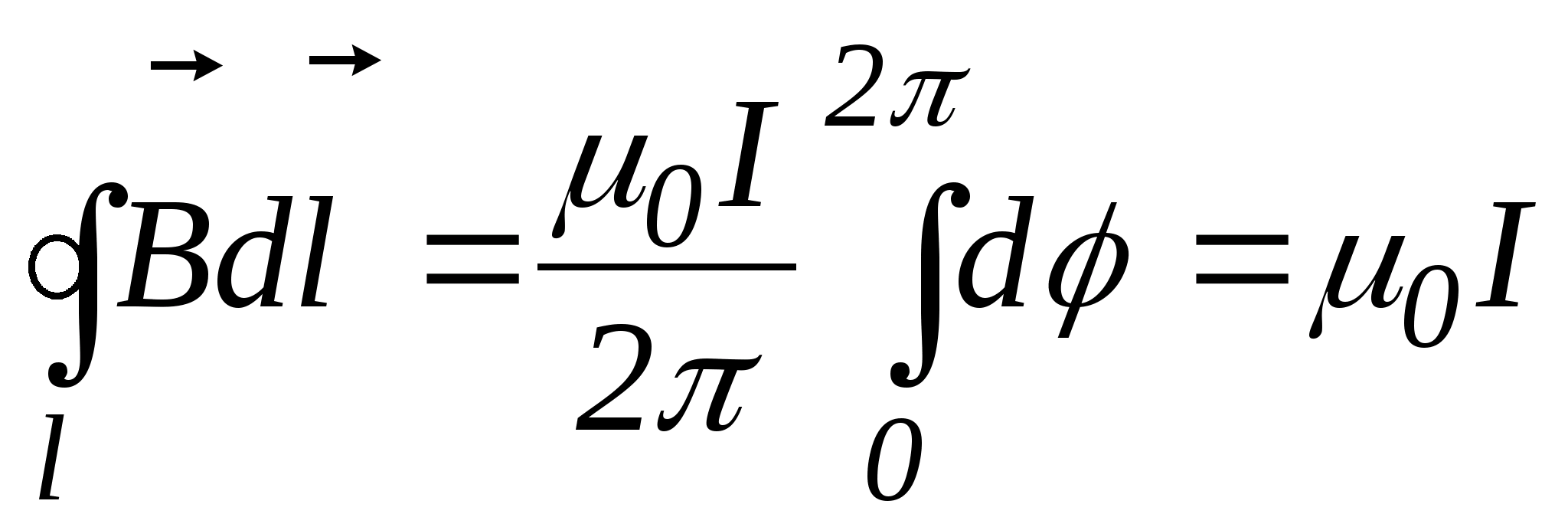 .
.
Обобщая полученный результат на случай произвольного количества токов в силу принципа суперпозиции ( 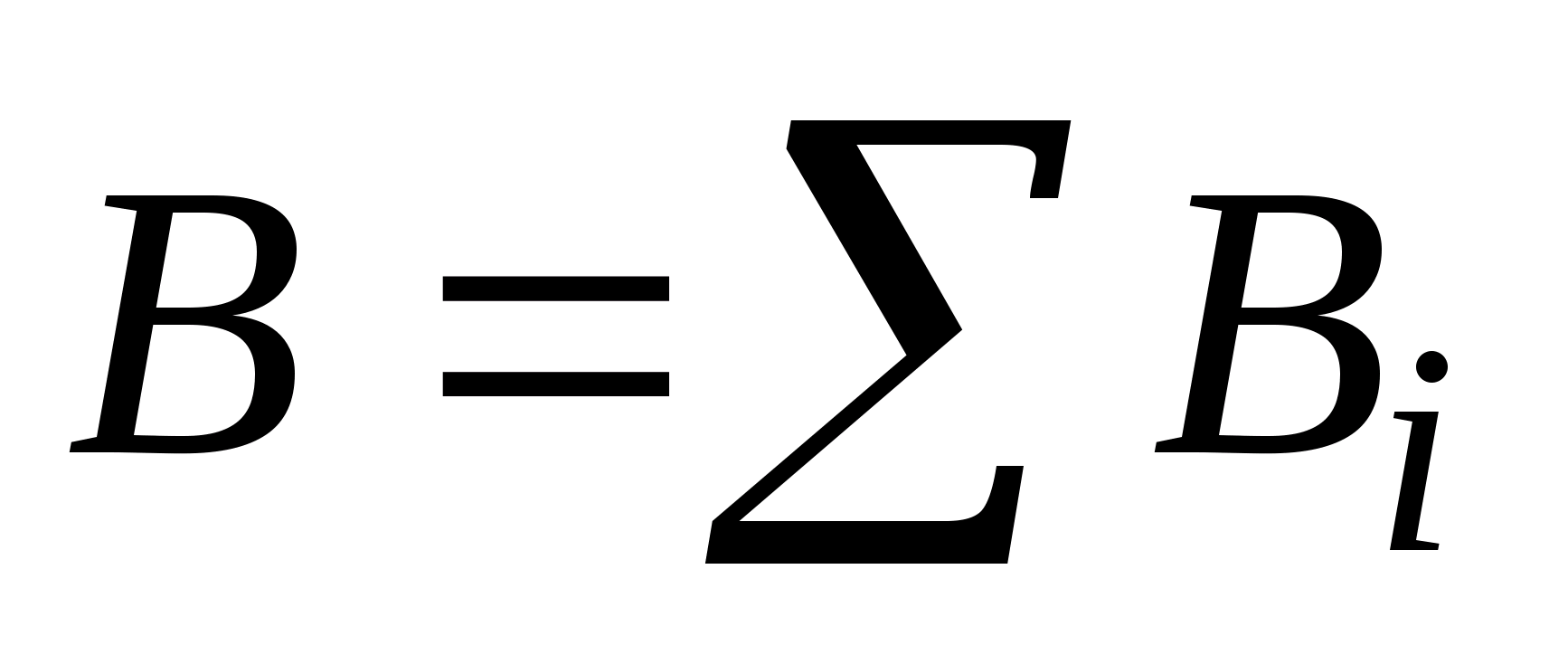 )
)
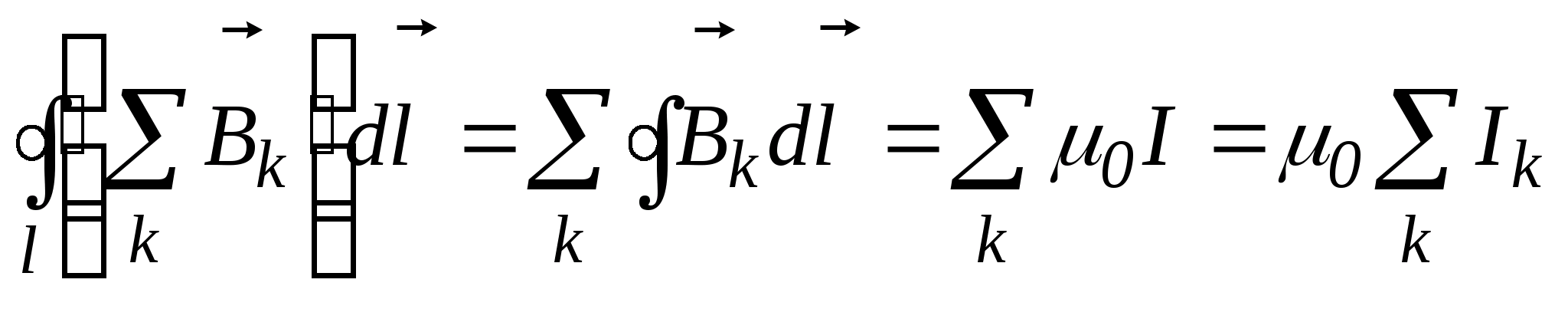 .
.
В результате получаем закон полного тока:
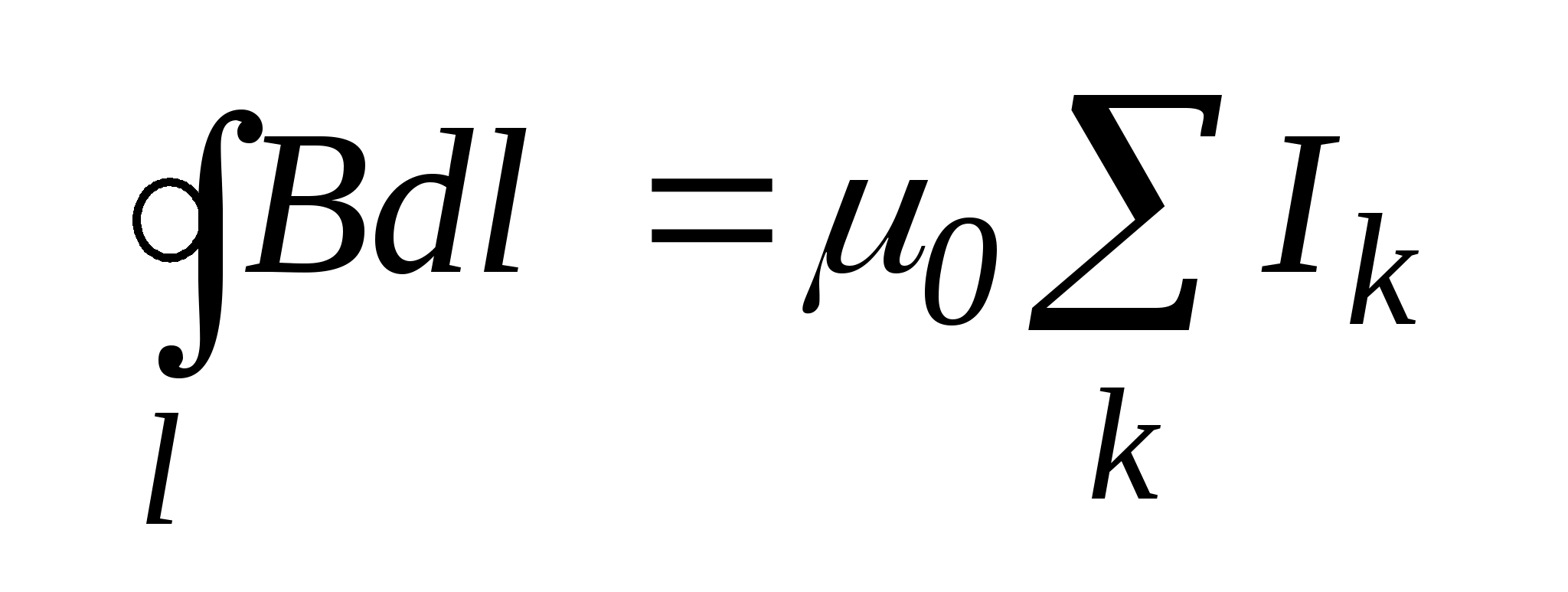
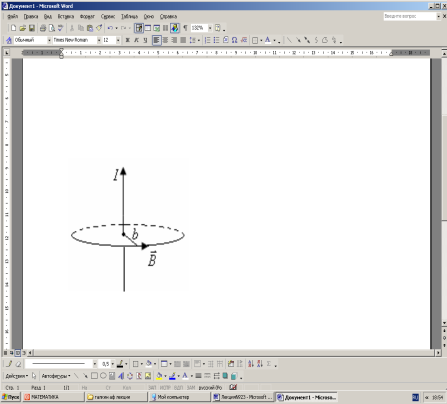 Циркуляция вектора магнитной индукции вдоль произвольного замкнутого контура прямо пропорциональна алгебраической сумме токов, охватываемых этим контуром.
Циркуляция вектора магнитной индукции вдоль произвольного замкнутого контура прямо пропорциональна алгебраической сумме токов, охватываемых этим контуром.
Например, применительно к полю бесконечного прямого тока:
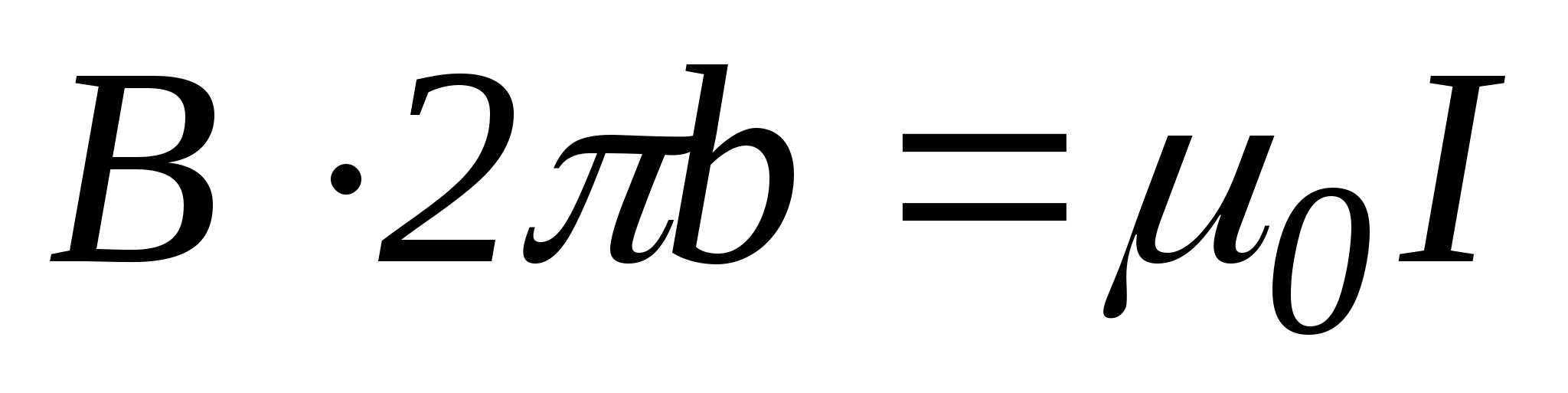
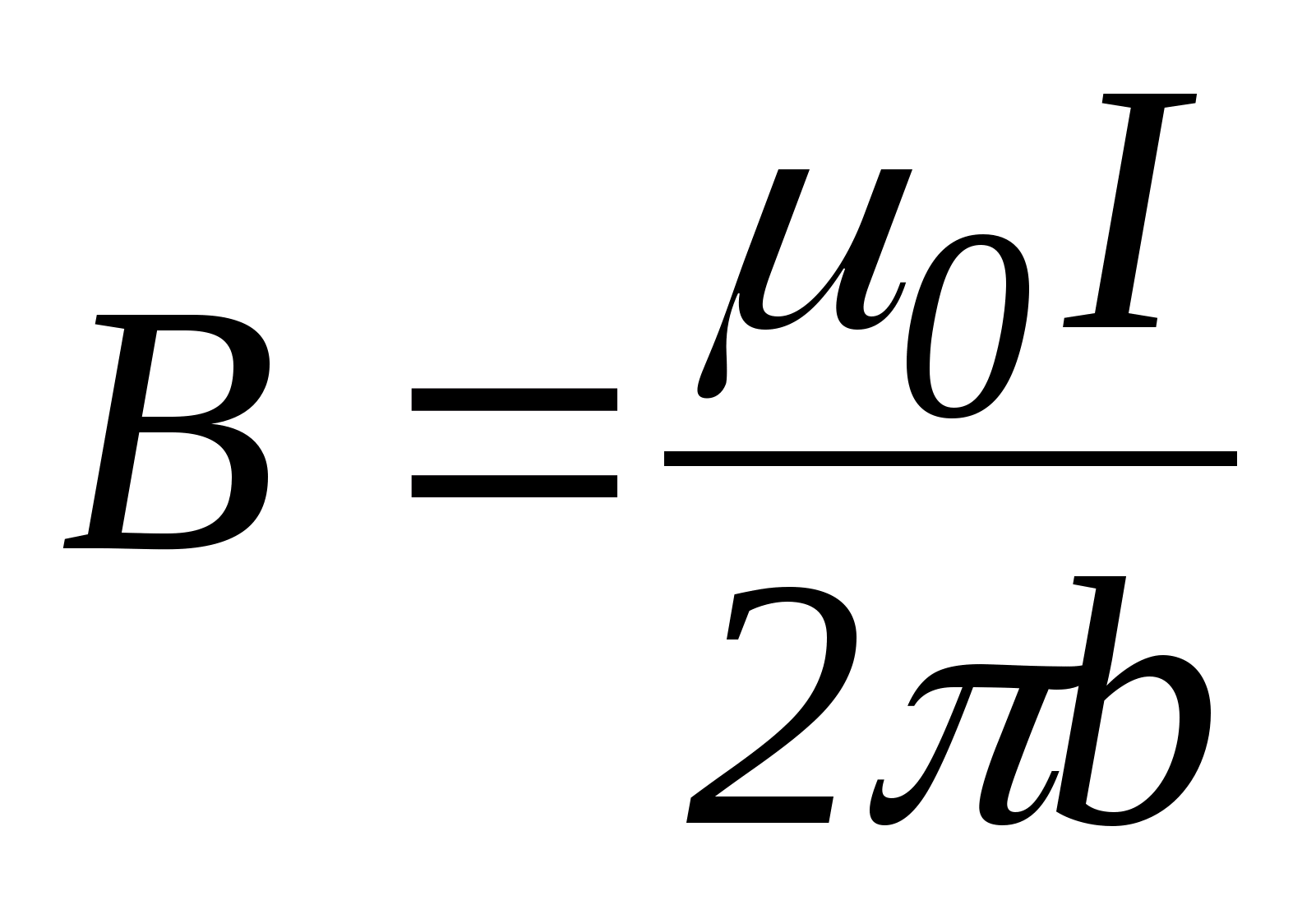 (очень просто!)
(очень просто!)
Агнитное поле длинного соленоида и тороида
а) Соленоид (от греч. «солен» - трубка) – провод, навитый в виде спирали на круглый цилиндрический каркас. Длинным можно считать соленоид, у которого длина в 5-6 раз больше диаметра. Пренебрегая концевыми эффектами, поле внутри соленоида можно считать однородным. Пусть число витков  , длина соленоида
, длина соленоида 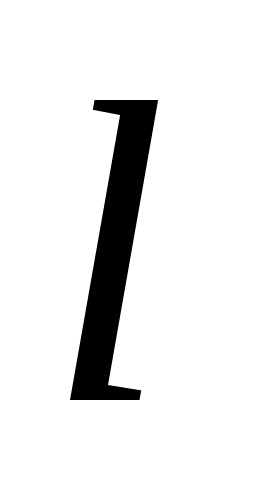 , ток
, ток 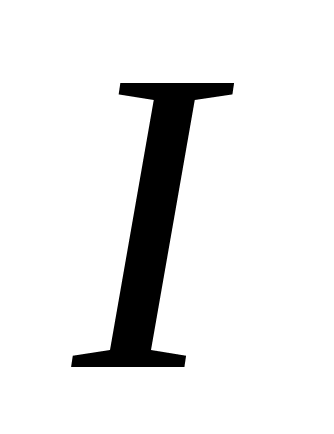 (рис. 23.9).
(рис. 23.9).
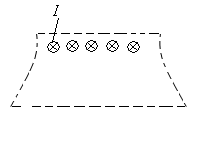
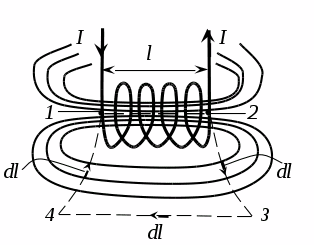 | Выберем контур таким образом, чтобы одна сторона была вдоль оси (1-2) соленоида, другая параллельна ей достаточно далеко (3-4), где  , и две стороны (2-3) и (4-1) перпендикулярны силовым линиям (из соображений симметрии ясно, что они направлены вдоль оси). Циркуляция: , и две стороны (2-3) и (4-1) перпендикулярны силовым линиям (из соображений симметрии ясно, что они направлены вдоль оси). Циркуляция: 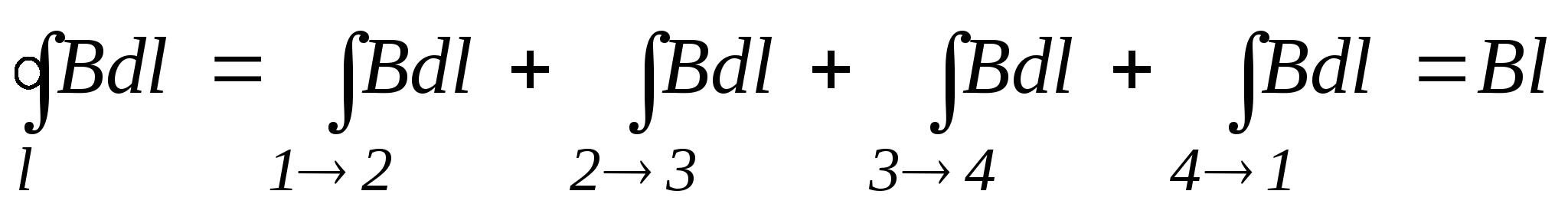 В соответствии с законом полного тока В соответствии с законом полного тока 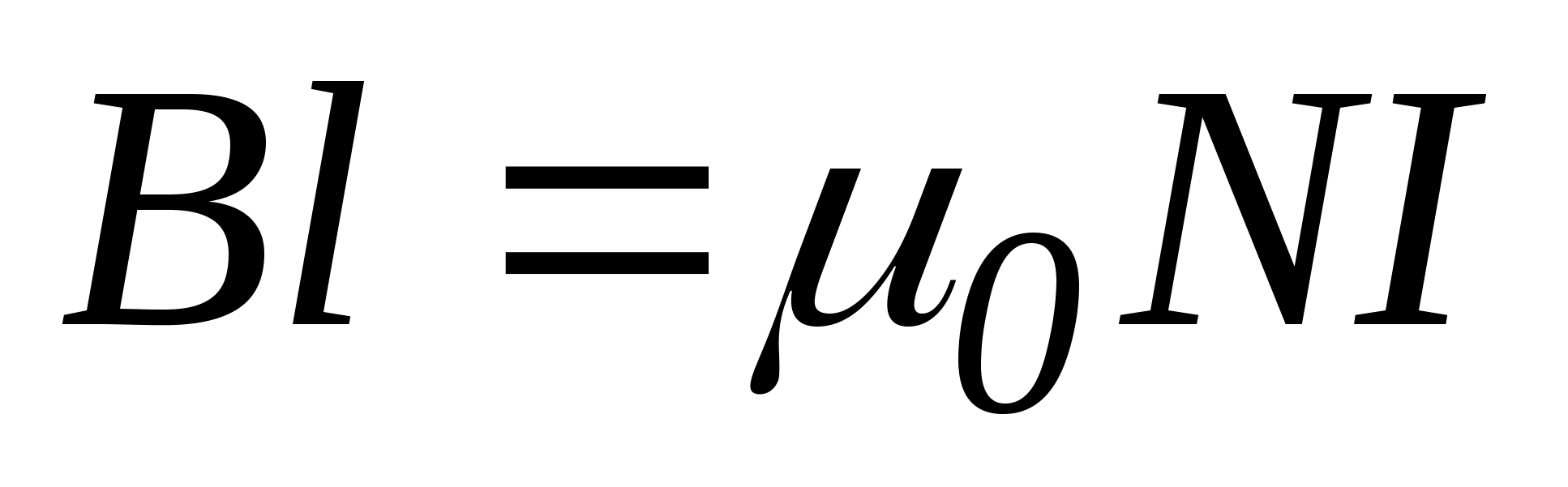 , , 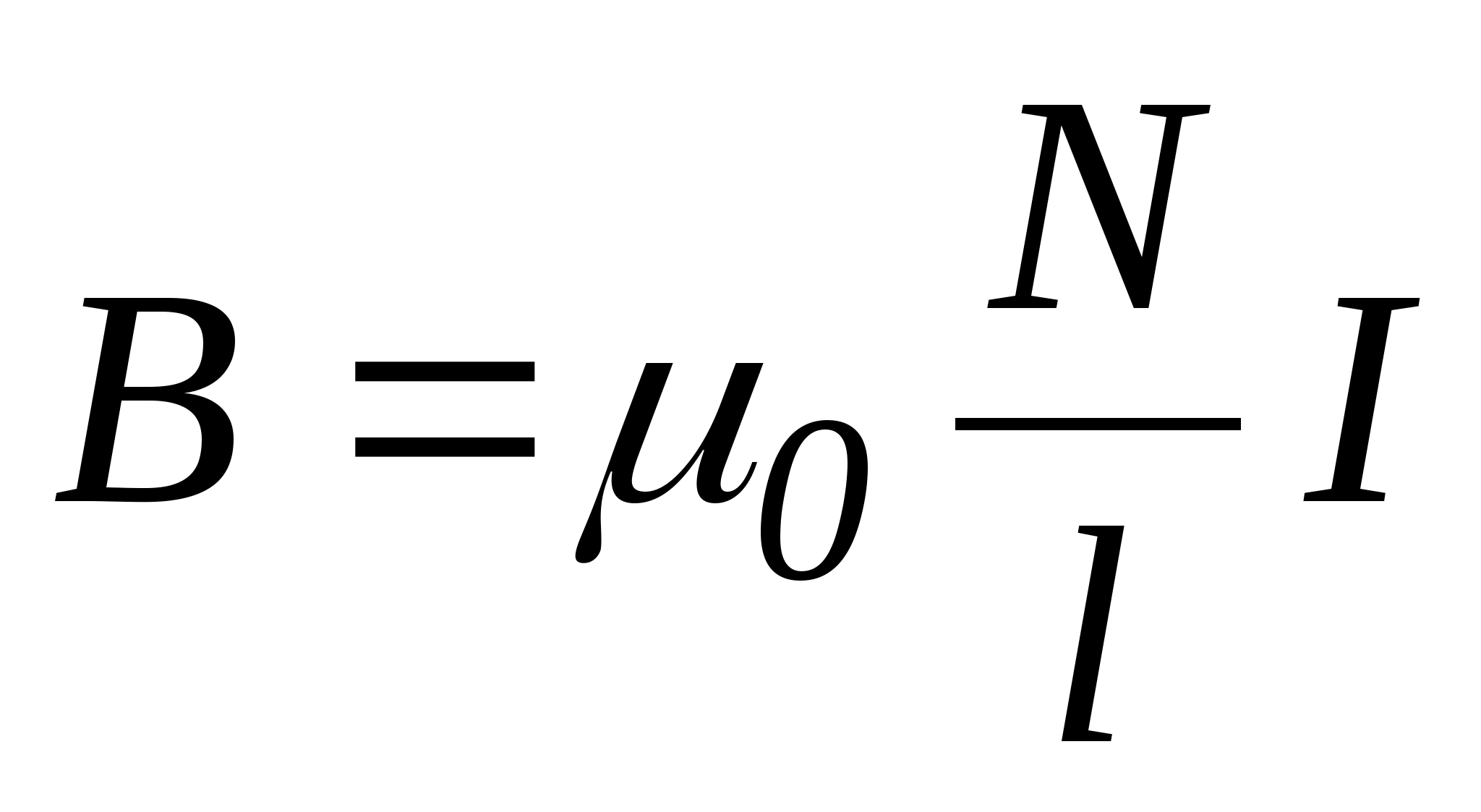 , итак, поле , итак, поле | |
| Рис. 23.9 | ||
 | соленоида: 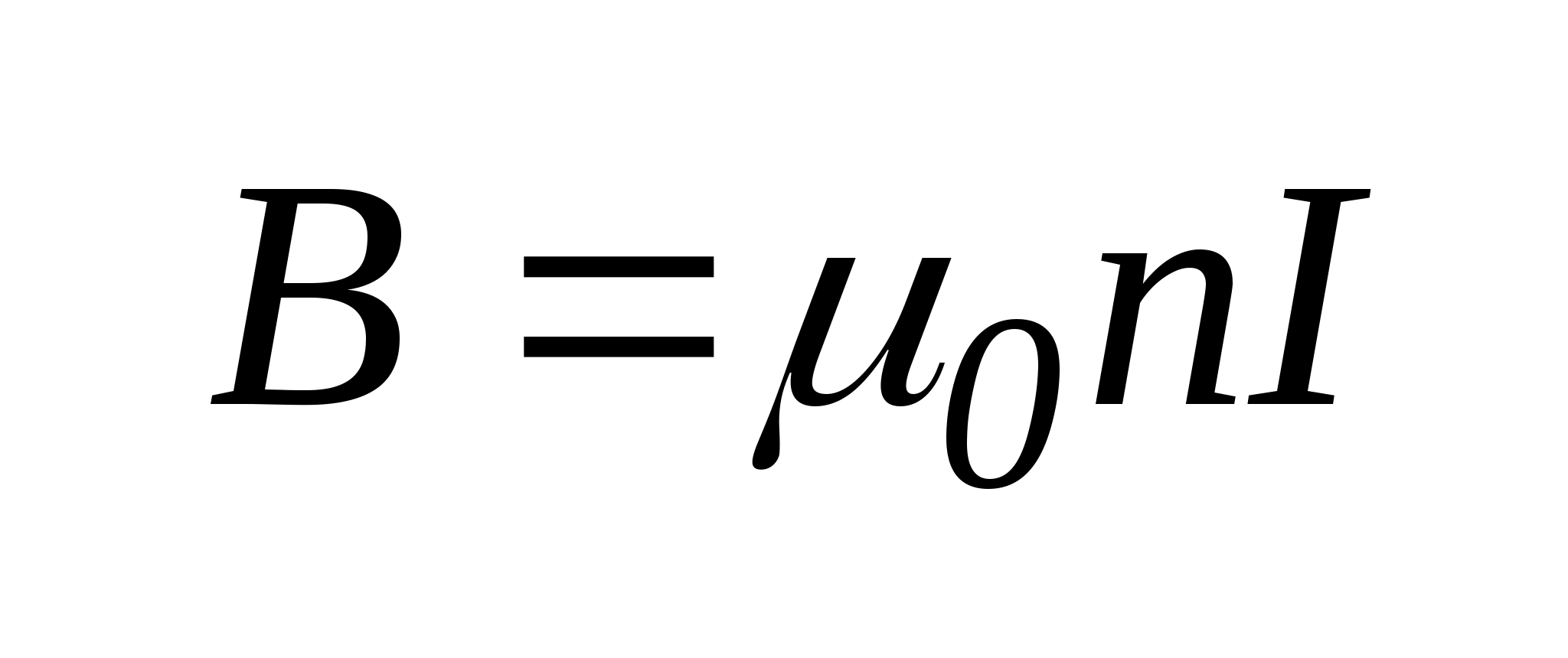 где где 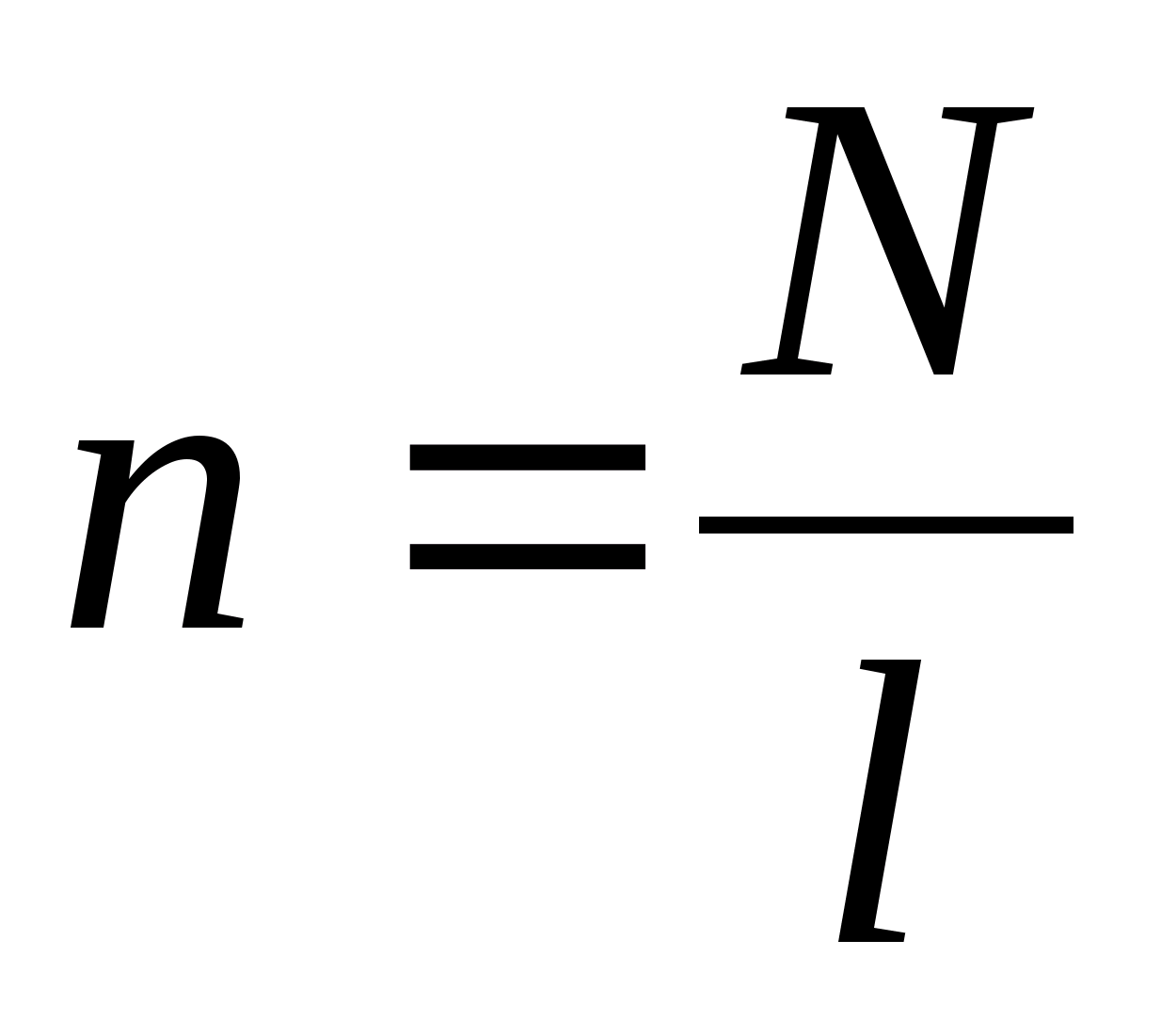 – число витков на единицу длины. – число витков на единицу длины. | |
| Рис. 23.10 |
б 
Рис. 23.11
) Тороид представляет собой провод, навитый как каркас, имеющий форму тора (рис. 23.11). Из соображений симметрии нетрудно понять, что силовые линии вектора 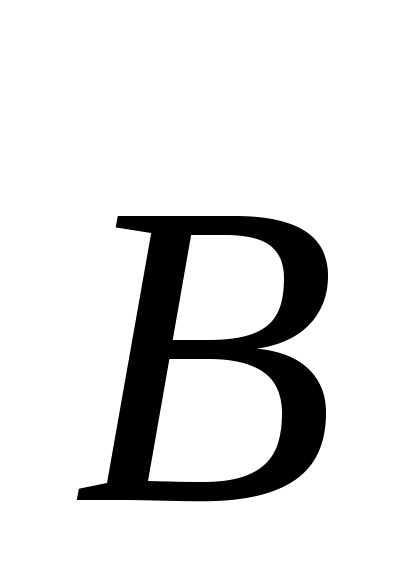 должны быть окружностями, центры которых расположены на оси тороида. Ясно, что в качестве контура следует взять одну из таких окружностей (показана пунктиром). Если контур расположен внутри тороида, он охватывает ток
должны быть окружностями, центры которых расположены на оси тороида. Ясно, что в качестве контура следует взять одну из таких окружностей (показана пунктиром). Если контур расположен внутри тороида, он охватывает ток  , где
, где  – число витков в тороидальной катушке;
– число витков в тороидальной катушке; 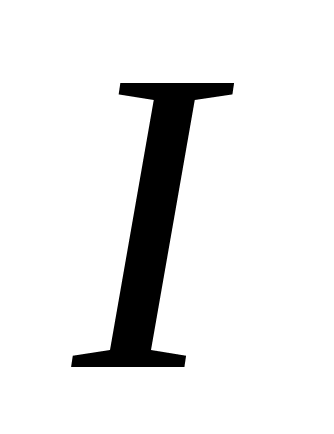 - ток в проводе. Пусть радиус контура
- ток в проводе. Пусть радиус контура 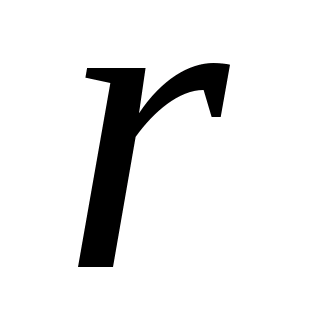 , тогда по теореме о циркуляции
, тогда по теореме о циркуляции 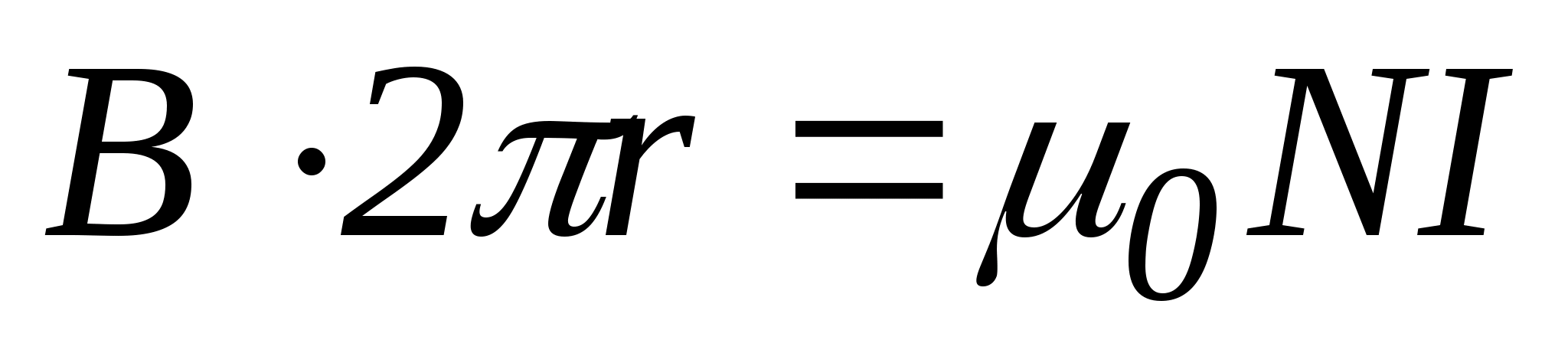 , откуда следует, что внутри тороида
, откуда следует, что внутри тороида 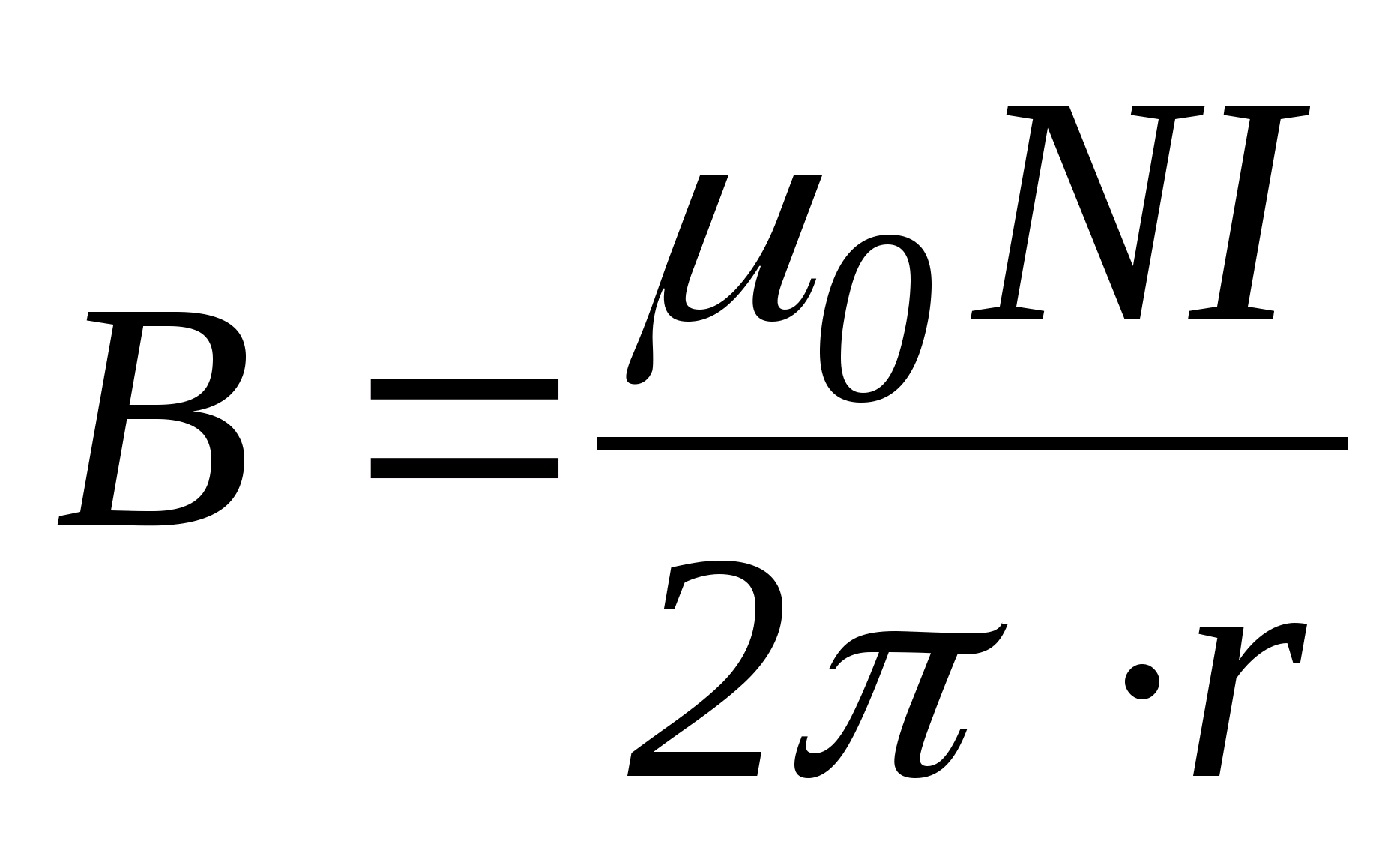 .
.
Будем считать 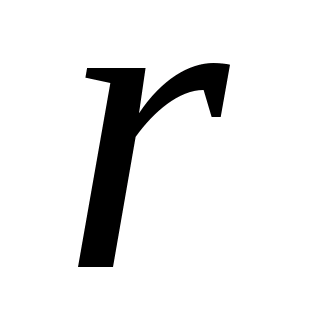 много больше толщины тороида, тогда
много больше толщины тороида, тогда 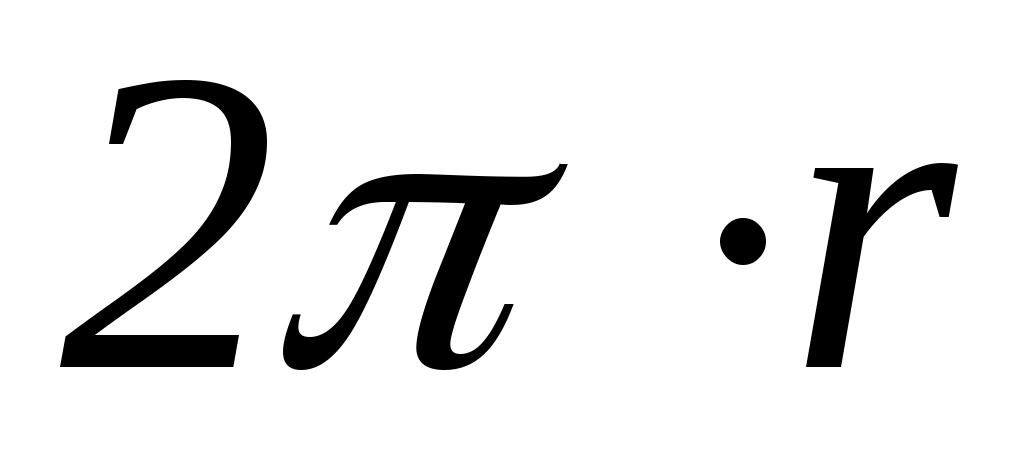 – длина тороида
– длина тороида 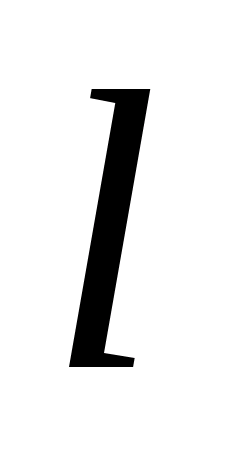 , поле тороида:
, поле тороида:
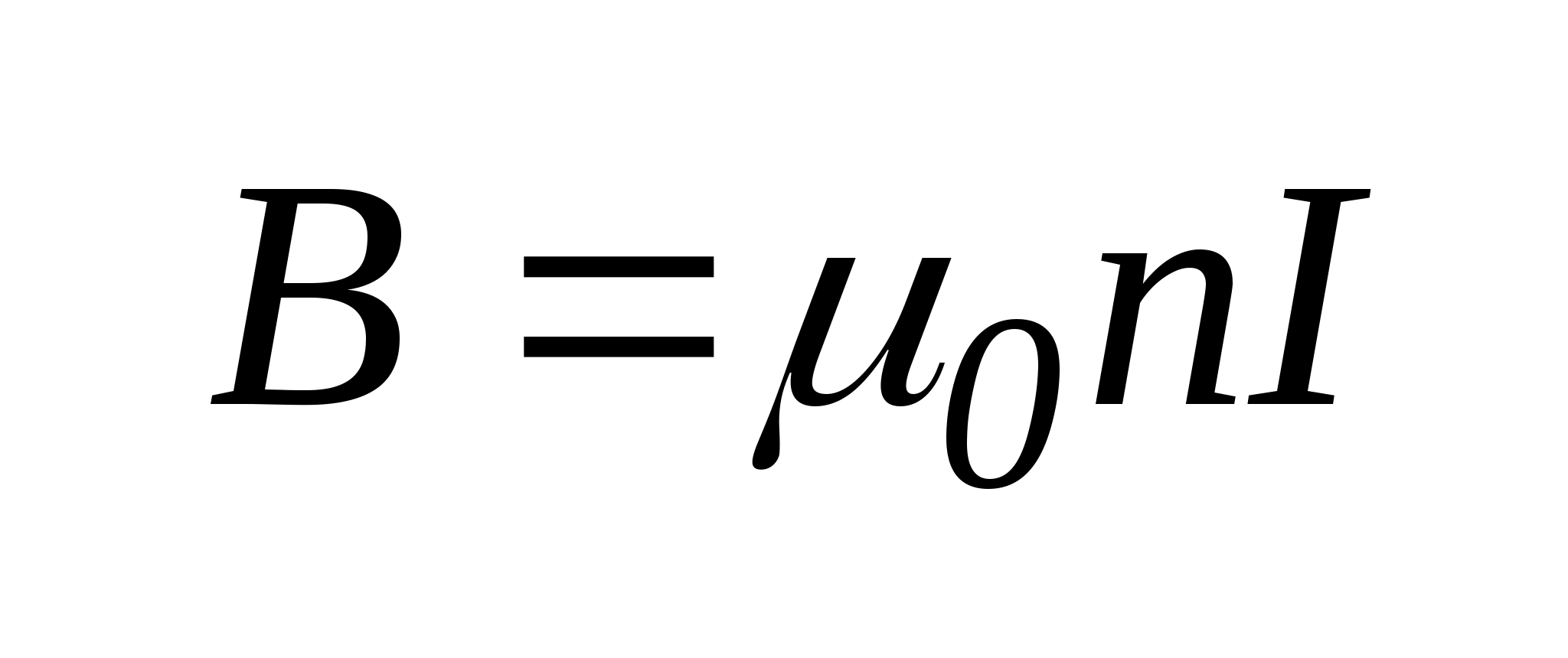
где 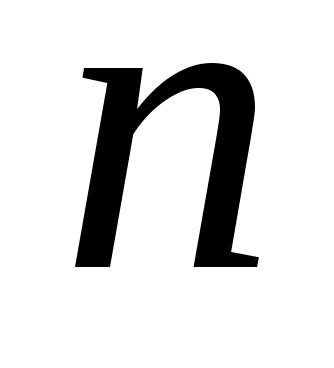 , как и для соленоида, число витков на единицу длины.
, как и для соленоида, число витков на единицу длины.
Магнитный поток
Автор: Субботин Б.П.
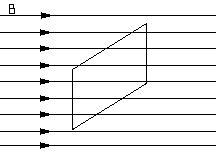
На картинке показано однородное магнитное поле. Однородное означает одинаковое во всех точках в данном объеме. В поле помещена поверхность с площадью S. Линии поля пересекают поверхность.
Определение магнитного потока:
Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.
Формула магнитного потока:
Ф = BS cos α
здесь α - угол между направлением вектора магнитной индукции B и нормалью к поверхности S.
Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.
А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 108 мкс. Соответственно 1 мкс = 10-8 вб.
Магнитный поток является скалярной величиной.
Потокосцепление
Р 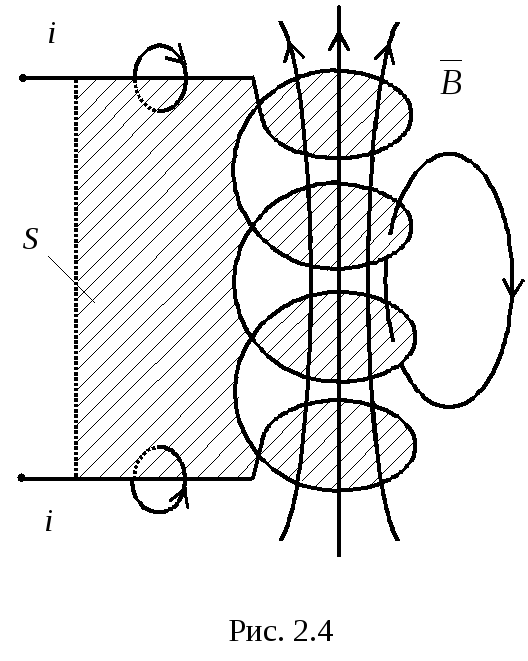 ассмотрим катушку с токомi, состоящую из нескольких витков (рис.2.4). Изобразим линии магнитной индукции, пересекающие поверхность
ассмотрим катушку с токомi, состоящую из нескольких витков (рис.2.4). Изобразим линии магнитной индукции, пересекающие поверхность 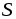 , ограниченную этим контуром, и образующие поток
, ограниченную этим контуром, и образующие поток 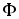 . Из рисунка видно, что различные силовые линии пересекают указанную поверхность различное число раз. Для учета этого обстоятельства используется такое понятие, какпотокосцепление
. Из рисунка видно, что различные силовые линии пересекают указанную поверхность различное число раз. Для учета этого обстоятельства используется такое понятие, какпотокосцепление 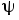 . Потокосцепление можно получить, умножая поток магнитной индукции на число витков, с которым он сцепляется,
. Потокосцепление можно получить, умножая поток магнитной индукции на число витков, с которым он сцепляется,
и складывая полученные произведения. При этом слагаемые берутся со знаком “плюс” для трубок, связанных с направлением тока правилом правого винта, в противном случае соответствующее слагаемое учитывается со знаком “минус”.
Э.д.с., индуктируемая в контуре, определяется величиной потокосцепления 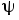 , поэтому
, поэтому
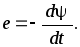
Если может быть принято допущение о том, что все линии магнитной индукции сцепляются со всеми 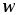 витками катушки, потокосцепление и магнитный поток связаны простым соотношением
витками катушки, потокосцепление и магнитный поток связаны простым соотношением