Называется потоком вектора напряженности через площадку dS

гдеЕ_n—проекция вектора напряжённости на нормаль n к площадке dS.

Единица потока вектора напряженности электростатического поля — 1 В×м.

Примечание.Полный поток вектора напряжённости электрического поля определяется интегрированием выражения для «элементарного» потока через площадку dSпо всей поверхностиS.

Немецким ученым К. Гауссом (1777—1855) была доказана теорем, определяющая поток вектора напряженности электрического поля сквозь произвольную замкнутую поверх­ность.

В соответствии с выводами предыдущего раздела, поток вектора напряженности 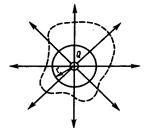сквозь сферичес­кую поверхность радиусаr, охватывающую точечный заряд Q, находящийся в ее центре, будет равен

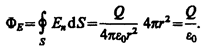
Этот результат справедлив для замкнутой поверхности любой формы.

Действительно, если окружить сферу произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд (рисунок слева), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее.

Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/e₀, т. е. теорема Гаусса не теряет справедливости.

Рассмотрим общий случай произвольной поверхности, окружающей nзарядов.

Вводя суммирование под знак интеграла, записываем, что

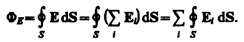
Согласно закону Гаусса, каждый из интегралов, стоящий под знаком суммы, равен Q_i /e₀.Следовательно,

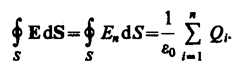
Полученная формула выражает теорему Гаусса для электростатического поля в вакууме:

поток вектора напряженности электростатического поля в вакууме сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e₀.

Примечание.В специальной литературе она также носит название теоремы Остроградского-Гаусса.

В общем случае электрические заряды могут быть размещены с некоторой объемной плотностью r=dQ/dV.. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V,

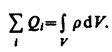
Используя эту формулу, теорему Гаусса можно записать так:

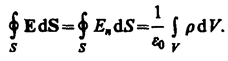
лектростатическое поле можно задать, указав для каждой точки величину и направление вектора 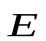. Совокупность этих векторов образует поле вектора напряженности электростатического поля. Графическое изображение электростатического поля с помощью вектора напряженности 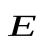в различных точках поля очень неудобно. Векторы напряженности при этом накладываются друг на друга, и получается весьма запутанная картина. Более наглядным является метод, предложенный М. Фарадеем изображения электростатических полей с помощью силовых линий напряженности.Силовые линии напряженности – это линии, касательные к которым в каждой точке совпадают с направлением вектора 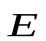.Линии напряженности направлены так же как вектор 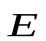поля в рассматриваемой точке. Например, на рис.2 линии напряженности направлены слева направо. Линии напряженности не пересекаются, т.к. в каждой точке поля вектор 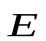имеет только одно определенное направление. Линии напряженности начинаются на положительном заряде и заканчиваются на отрицательном.Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям напряженности, было равно численному модулю вектора 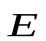.Тогда по картине линий напряженности можно судить о направлении и значении вектора 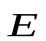в разных точках пространства (рис. 2.1).

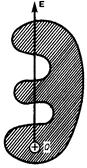
Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению, т.е. 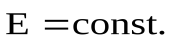Однородное электростатическое поле изображается параллельными силовыми линиями на равном расстоянии друг от друга (такое поле существует, например, между пластинами конденсатора) (рисунок ).

В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из бесконечности входят в отрицательный заряд. Т.к. 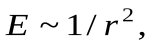то и густота силовых линий обратно пропорциональна квадрату расстояния от заряда. Однако площадь поверхности сферы, через которую проходят эти линии сама возрастает пропорционально квадрату расстояния, поэтому общее число линий остается постоянным на любом расстоянии от заряда.

Для системы зарядов, как видим, силовые линии направлены от положительного заряда к отрицательному (рисунок 2.2).

Рисунок 2.2

Из рисунка 2.3 видно, так же, что густота силовых линий может служить показателем величины .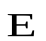

Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их число, которое равно модулю вектора напряженности 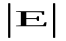, т.е.

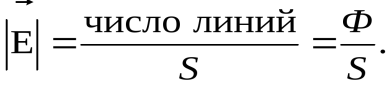
Пример 1: если на рисунке 2.3 выделить площадку, 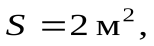то напряженность изображенного поля будет равна

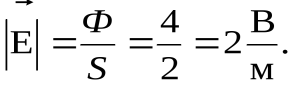
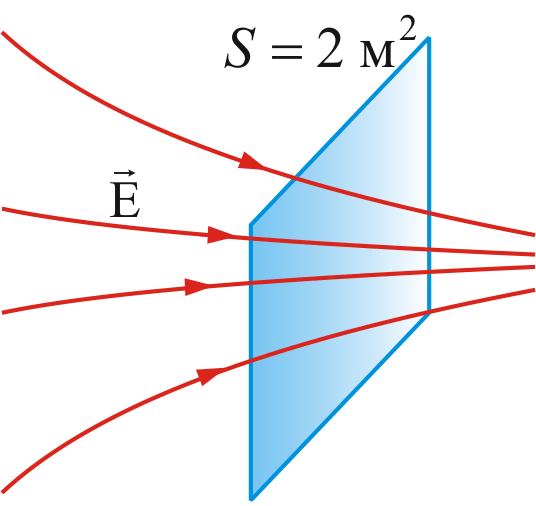
Рисунок 2.3

Пример 2: площадка 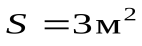находится в однородном поле Сколько линий пересекает эту площадку, если угол составляет 30º (рисунок 2.4).

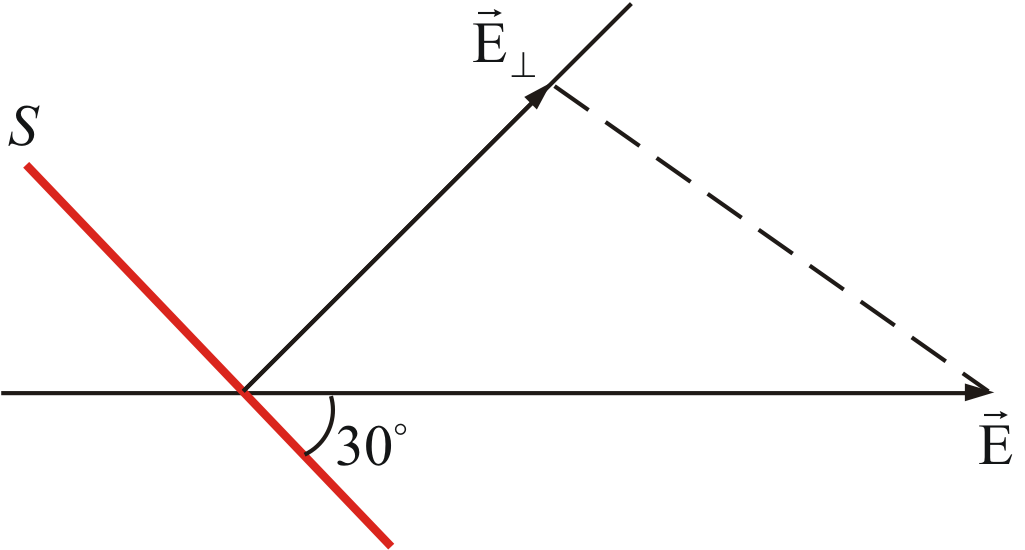
Рисунок 2.4

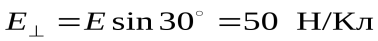
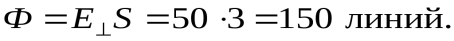
2.3. Теорема Остроградского – Гаусса (теорема Гаусса)

К.Ф. Гаусс (1777–1855) выдающийся немецкий математик, астроном и физик в 1839г. предложил теорему, которая устанавливает связь потока вектора напряженности электрического поля через замкнутую поверхность со значением зарядаq, находящегося внутри этой поверхности.Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :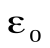

.

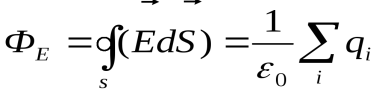Докажем эту теорему. Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностьюSпроизвольной формы. Разобьем замкнутую поверхность на элементарные площадкиdS, к каждой из которых проведем вектор нормали .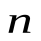

Э лементарный поток вектора напряженности через площадкуdS(рис. 2.8) определится соотношением:

,

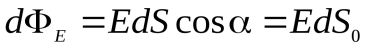где 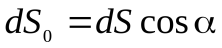–проекция 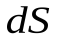на направление нормали 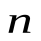. Тогда 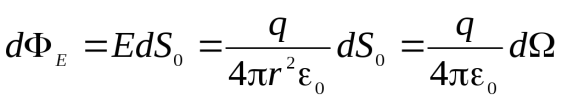, где 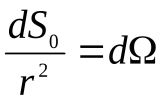- элементарный телесный угол, под которым элемент 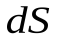виден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхностьSот точечного зарядаq, находящегося внутри этой поверхности.

,

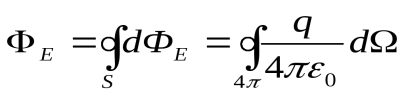
так как 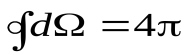, то

.

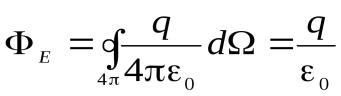Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS₁иdS₂, находящиеся внутри телесного углаdΩ(рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда 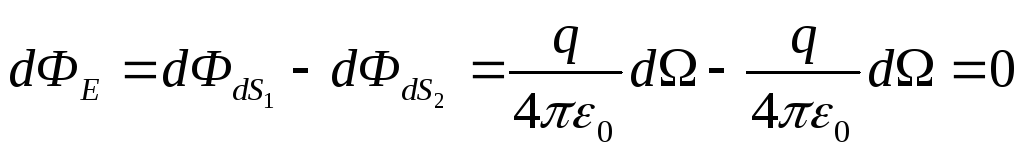, следовательно, поток напряженности электрического поля через любую поверхностьS, не охватывающую заряды равен нулю, т.е.Ф_Е=0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен .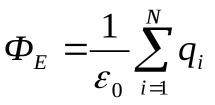

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :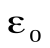

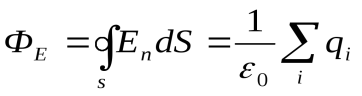(1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью 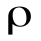, то теорема Гаусса имеет вид:

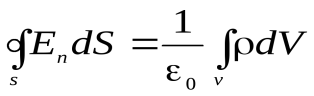(2)

где интеграл справа берется по объему V, охватываемому поверхностьюS.

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле 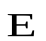зависит от конфигурации всех зарядов, поток 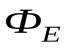сквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхностиS. Это значит, чтоесли передвинуть заряды внутри замкнутой поверхности, то 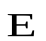изменится всюду, и на поверхностиS, апоток вектора 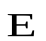через эту поверхность останется прежним.

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 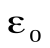, то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

Рассмотрим примеры применения теоремы Гаусса.