Проекция вектора напряжённости электрического поля на данное направление равна быстроте изменения потенциала в этом направлении, взятой с обратным знаком.

Или используя понятие градиента скалярной величины grad U:` 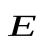= - grad U,

т.е. напряженность в какой-либо точке электростатического поля равна градиенту потенциала в этой точке, взятому с обратным знаком.

В общем случае потенциал U - функция всех трёх декартовых координат рассматриваемой точки поля, причёмgrad U = ( U/ X) + ( U/ Y) + ( U/ Z) .

Поэтому проекции вектора 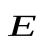на оси координат связаны с потенциаломполя т.o.: E_x = - U/ X;E_Y = - U/ Y;E_Z = - U/ Z;

Если заряд перемещается в направлении dl, перпендикулярном силовой линии, т.е. перпендикулярно ` 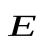, то соs (Е,dl) = 0, Е_l = 0 и dU/dl = 0 или U=const.

Следовательно, во всех точках кривой, ортогональной к силовым линиям, потенциал одинаков.

Геометрическое место точек с одинаковым потенциалом называется эквипотен­циальной поверхностью.

Т.к. потенциал постоянен лишь вдоль кривых, ортогональных к сило­вым линиям поля, то и эквипотенциальные поверхности должны быть везде ортогональны к силовым линиям. Очевидно, что работа, совершаемая при перемещении электрического заряда по одной и той же эквипотенциальной поверх­ности , равна нулю.

Электрическое поле можно изобразить графически не только при помощи силовых линий, но и при помощи эквипотенциальных поверхностей. Вокруг каж­дой системы зарядов можно провести бесконечное множество эквипотен­циальных поверхностей. Обычно их проводят т.о., чтобы разности потен­циалов между любыми двумя соседними эквипотенциальными поверхно­стями были одинаковыми.

Зная расположение силовых линий электрического поля, можно построить эквипо­тенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно в каждой точке поля определить абсолютное значение и направление вектора напряжённости электростатического по­ли.

Густота эквипотенциальных линий пропорциональна напряжённости поля: там, где больше Е, там и эквипотенциальные линии расположены теснее друг к другу.

Геометр место точ с одинаковой потенциальностью наз эквипотен­циальной пов-ю.

Т.к. потенциал постоянен лишь вдоль кривых, ортогональных к сило­вым лин поля, то и эквипотенц пов-ти должны быть везде ортогональны к силовым линиям. Раб, совершпри перемещ эл заряда по одной эквипотенциальной пов-ти = 0.

Эл поле можно изобраз графич не только при пом силовых линий, но и при пом эквипотенц пов-тей. Вокруг каж­д сист зарядов можно провести бесконеч множ-во эквипотен­ц пов-тей. Обычно их проводят т.о., чтобы разности потен­ц между люб 2 соседн эквипотенц пов-ми были одинаковыми.

Зная располож силов лин эл поля, можно построить эквипо­тенц пов-ти. и, наоборот, по известн располож эквипотенц поверхностей можно в кажд точке поля определ абсолютн знач и направл вектора напряжённости электростат по­ля.

Густота эквипотенц линий пропорц напряж-ти поля: там, где больше Е, там и эквипотенц лин располож теснее друг к др.

Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом —энергетической характеристикой поля. Работа по перемещениюединичного точечного положительного заряда из одной точки поля в другую вдоль осих при условии, что точки расположены бесконечно близко друг к другу иx₁–x₂= dx, равнаE_xdx. Та же работа равнаj₁-j₂=dj. Приравняв оба выражения, можем записать

(85.1)

где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осейyиz, можем найти вектор Е:

где i,j,k— единичные векторы координатных осей х, у,z.

Из определения градиента следует, что

т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал jимеет одно и то же значение.

Если поле создается точечным зарядом, то его потенциал, согласно, . Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы. С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного зарядаперпендикулярны эквипотенциальным поверхностям.

Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд,всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Евсегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим поверхностям.

Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности рас положены гуще, напряженность поля больше.

Итак, зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно определить в каждой точке поля модуль и направление напряженности поля. На рис. для примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного заряда (а) и заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом — впадину (б).

Величина