Затухающие колебания. Декремент затухания, коэффициент затухания, время релаксации

Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины.

Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими.

Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения

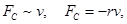
где r - коэффициент сопротивления среды. Знак минус показывает, что F_C направлена в сторону противоположную скорости.

Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона

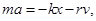
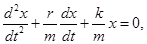
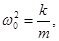
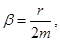
где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

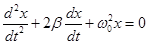
- дифференциальное уравнение затухающих колебаний.

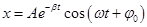
- уравнение затухающих колебаний.

ω – частота затухающих колебаний:

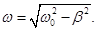
Период затухающих колебаний:

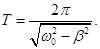
З 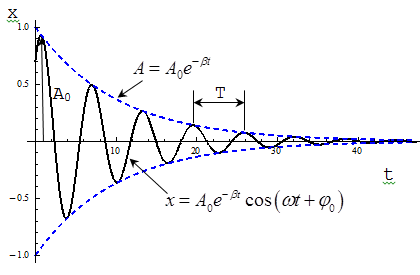атухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово­рить, когда β мало.

Если затухания выражены слабо (β→0), то 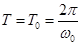. Затухающие колебания можно

рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону

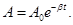
В уравнении (1) А₀ и φ₀ - произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания

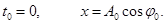
Рассмотрим колебание в течение, некоторого времени τ, за которое амплитуда уменьшится в е раз

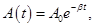
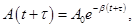
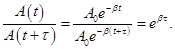
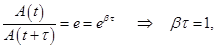
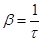
τ - время релаксации.

Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затуханияD, который равен отношению амплитуд, отстоящих по времени на период:

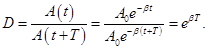
Логарифмический декремент затухания равен логарифму D:

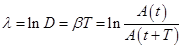
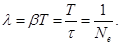
Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний умень­шилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина.

Еще одной характеристикой колебательной система является добротность Q.

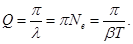
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ.

Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

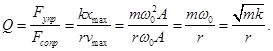
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Пусть

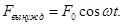
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

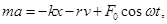
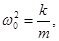
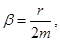
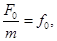
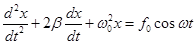(1)

- дифференциальное уравнение вынуж­денных колебаний.

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения. Разложение сложного колебания в ряд Фурье. Спектральный анализ. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.