Геометрический смысл двойного интеграла

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ…………………………………………………….4

1. КРАТНЫЕ ИНТЕГРАЛЫ…………………………………..5

1.1. Двойные интегралы……………………………………….5

1.2. Тройные интегралы………………………………………13

2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ………………………21

2.1. Криволинейные интегралы первого рода……………….21

2.2. Криволинейные интегралы второго рода……………….23

3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ……………………….29

3.1. Поверхностные интегралы первого рода………………..29

3.2. Поверхностные интегралы второго рода………………..36

4. ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ………………………44

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………..45

ПРИЛОЖЕНИЕ………………………………………………..46

ВВЕДЕНИЕ

В программу по высшей математике для большинства технических специальностей входит выполнение курсовой работы. Она приходится на третий семестр, когда студенты изучают кратные, криволинейные и поверхностные интегралы, а на их основе – теорию поля. Именно по этим разделам и составлена курсовая работа.

В курсовой работе требуется рассчитать технические параметры модели летательного аппарата. Подобные вычисления могут потребоваться при решении реальных инженерных задач, где необходимо исследовать оболочки или однородные объекты из различных материалов с точки зрения механики, а также воздействие внешних потоков среды или поля, что пересекается с задачами физики.

Сложность выполнения курсовой работы связана с необходимостью изучения большого объема материала из различных разделов высшей математики.

Методические указания содержат необходимые теоретические основы математики, особое внимание уделено физическим и техническим приложениям. Конечно, для более глубокого понимания теории потребуется изучение литературы, но все необходимые для курсовой работы определения и формулы в этих указаниях приведены. Дано много различных примеров с подробными решениями, часть рассматриваемых задач идентична заданиям курсовой работы, что облегчит ее выполнение.

Указания соответствуют уровню преподавания курса и могут быть использованы также и как конспект лекций.

КРАТНЫЕ ИНТЕГРАЛЫ

ДВОЙНЫЕ ИНТЕГРАЛЫ

Рис. 1.1

Пусть D - ограниченная замкнутая область в плоскости xOy. Функция z=f(x,y) определена и ограничена в области D (рис.1.1). Разобьем эту область на n частей и обозначим их площади соответственно ∆S₁, ∆S₂, ∆S₃, . . . , ∆S_n. В каждой части ∆S_i возьмем произвольно точку M_i (x_i, y_i) и составим сумму

. (1.1)

Эта сумма называется интегральной суммой функции f(x, y) в области D.

Определение. Если при любом разбиении области D на части ∆S_i и произвольном выборе точек M_i(x_i,y_i) существует предел последовательности сумм (1.1) при условии, что максимальный из диаметров частей ∆S_i стремится к нулю, то этот общий предел называют двойным интегралом от функции f(x, y) по области D и обозначают символом

.

Итак,

.

Область D называется областью интегрирования, а dS – элементом площади.

Свойства

Двойной интеграл обладает всеми основными свойствами обыкновенного интеграла функции одной переменной на отрезке.

1. Постоянный множитель можно выносить за знак двойного интеграла,

.

2. Двойной интеграл от суммы функций равен сумме двойных интегралов,

.

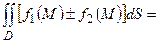
3. Область интегрирования можно разбить на части (рис.1.2),

.

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

ПЕРВОГО РОДА

Рис. 2.1

Пусть в пространстве имеется некоторая гладкая кривая АВ, в каждой точке которой задана непрерывная функция f(x,y,z) (рис. 2.1). Пусть {l_i} - произвольное разбиение кривой АВ на n частей. Выберем в каждой дуге произвольным образом точку M_i и составим сумму

. (2.1)

Определение.Предел интегральных сумм (2.1) при стремлении максимального диаметра разбиения к нулю называется криволинейным интегралом первого рода от функции f по кривой АВ и обозначается

.

Таким образом, .

Криволинейный интеграл первого рода также называют криволинейным интегралом по длине дуги или от скалярной функции.

Необходимо отметить, что криволинейный интеграл первого рода не зависит от направления кривой АВ. Обычный определенный интеграл является частным случаем криволинейного, когда кривая интегрирования совпадает с осью Ox.

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

ВТОРОГО РОДА

Пусть в пространстве заданы: направленная гладкая кривая АВ, функция P(x, y, z) на этой кривой, {l_i} - произвольное разбиение кривой АВ, точка M_iÎl_i, Dx_i - проекция дуги l_i на ось Ох.

Определение. Предел интегральных сумм

,

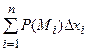если максимальный диаметр разбиения {l_i} стремится к нулю, называется криволинейным интегралом второго рода по координате x и обозначается

.

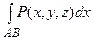Аналогично определяются криволинейные интегралы по координатам у и z, их обозначают

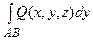и .

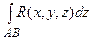Определение. Интеграл

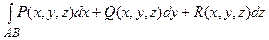
называется общим криволинейным интегралом второго рода или криволинейным интегралом по координатам.

Отметим, что при изменении направления кривой АВ криволинейный интеграл второго рода меняет свое значение на противоположное, т.е.

= .

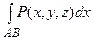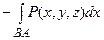Формула Грина

Если C – граница области D и функции P и Q вместе со своими частными производным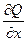и и 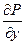непрерывны в области D, то справедлива формула Грина:

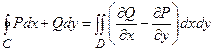, (2.3)

контур обходится так, чтобы область оставалась слева (пример 2.2).

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

ПЕРВОГО РОДА

Рис. 3.1

Пусть заданы некоторая непрерывная функция F(x, y, z) и гладкая поверхность S, определяемая явным уравнением z = f(x, y), пусть область D - проекция поверхности S в плоскости хОу (рис. 3.1). Разобьем произвольным образом поверхность S на n элементов и обозначим i-ый элемент - Ds_i, в каждом из них выберем произвольную точку M_i. Составим сумму

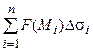. (3.1)

Определение. Поверхностным интегралом первого рода называется предел интегральных сумм (3.1) при стремлении максимального диаметра площадок Ds_i к нулю, т.е.

.

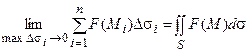Поверхностный интеграл первого рода называют также поверхностным интегралом от скалярной функции.

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

ВТОРОГО РОДА

Пусть в каждой точке поверхности S определен некоторый вектор или задано векторное поле

,

где P, Q, R - непрерывные функции, и пусть - единичный вектор нормали к поверхности.

Определение. Предел интегральных сумм

Рис. 3.4

при стремлении максимального диаметра площадок Ds_i к нулю называется поверхностным интегралом второго рода или поверхностным интегралом от векторной функции,

.

Координаты единичного вектора нормали есть направляющие косинусы, т.е.

,

тогда скалярное произведение можно расписать через координаты

.

Произведение ∆σ ·cosα есть проекция площадки ∆σ на плоскость yOz, т.е. ∆σ_yz. Аналогично получим остальные проекции,

.

Суммируя и переходя к пределу, запишем поверхностный интеграл второго рода в другом виде, по координатам

, (3.7)

где S⁺ - сторона поверхности, задаваемая направлением нормали .

При переходе к другой стороне S ^- поверхности S интеграл второго рода меняет знак на противоположный.

ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

1. Оболочка S летательного аппарата представляет собой полую тонкостенную конструкцию, выполненную из композиционного материала с поверхностной плотностью g(x, y, z) (координаты даны в метрах, поверхностная плотность - кг/м²). Вычислить:

а) массу оболочки m₀;

б) координаты центра тяжести C₀(x_c0, y_c0, z_c0);

в) моменты инерции оболочки относительно координатных осей I_x0, I_y0, I_z0.

2. Укомплектованный, готовый к запуску аппарат можно считать однородным с пространственной плотностью m₁ = const (кг/м³), т.е. массу оболочки не учитывать. Вычислить:

а) массу аппарата m₁;

б) координаты центра тяжести C₁(x_с1, y_с1, z_с1);

в) моменты инерции аппарата относительно координатных осей I_x1, I_y1, I_z1.

3. Летательный аппарат находится в потоке частиц, движущихся со скоростью (x, y, z) (м/c). Вычислить массу частиц m, бомбардирующих боковую поверхность аппарата в единицу времени, если плотность вещества в потоке m₂ = const (кг/м³).

4. Теплота сгорания топлива q =10² МДж/кг, КПД двигателей h= 60%. Рассматривая летательный аппарат как материальную точку, найти массу горючего M, необходимого для перемещения аппарата в силовом поле 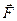(x, y) вдоль траектории L от точки A до точки B (сила 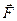дана в килоньютонах, координаты - в километрах).

Данные по вариантам приведены в приложении.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Пискунов, Н. С. Дифференциальное и интегральное исчисления: в 2 т. / Н. С. Пискунов. – Т. 2. – М.: Наука, 1985.

2. Смирнов, В. И. Курс высшей математики: в 8 т. / В. И. Смирнов. – Т. 2. – М.: Наука, 1965.

3. Шестаков, А. А. Курс высшей математики / А. А. Шестаков. – М.: Высш. шк., 1981.

4. Слободецкий, Л. Н. Интегральное исчисление / Л. Н. Слободецкий. – М.: Высш. шк., 1974.

5. Бронштейн, И. Н. Справочник по математике для инженеров и учащихся втузов / И. Н. Бронштейн, К. А. Семендяев. – М.: Наука, 1980.

6. Данко, П. Е. Высшая математика в упражнениях и задачах: в 2 ч. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова и др. – Ч. 2. – М.: Высш. шк., 1980.

7. Письменный, Д. Т. Конспект лекций по высшей математике: в 2 ч. / Д. Т. Письменный. – Ч. 2. – М.: Рольф, 2001.

Приложение

ВАРИАНТЫ ЗАДАНИЙ

№	Поверхность S	Поверх. плотность γ(x, y, z)	Поле скоростей (x, y, z)	Силовое поле (x, y)	Траектория L
	x2 + y2 = 1, z = 2, z = 0	x2	(-x; -y; z)	(x – y; 1)	x2 + y2 = 4, y > 0, A(-2;0), B(2;0)
	, z = 4	y2	(-x; -y; z)	(x –y; x +y)	, y > 0, A(-3;0), B(3;0)
	x2 + y2 + z2 = 4, z > 0	z + 1	(y; -x; 0)	(y2; x)	y = 4x, A(2;8), B(0;0)
	2z = 4 – (x2 + y2), z = 0	x2	(-x; -y; -2z)	(x2y; -y)	отрезок AB, A(-1;0), B(0;1)
	, z = 0	y2	(-x; -y; -z)		y = 2 , A(1;2), B(0;0)
	x2 + y2 = 2z, z = 1/2	x2	(x; y; 2z +10)	(xy - y2; x)	y = 2x2, A(1;2), B(0;0)
	x2 + y2 = z2, z > 0, z = 1	x2	(x - 5; y; z)	(y2 - y; 2xy)	x2 + y2 = 9, y > 0, A(-3;0), B(3;0)
	x2 + y2 + z2 = 9, z > 0	x2	(0; 0; z2 –16)	(xy; 2)	y = sin x, A(π;0), B(0;0)
	y2 + z2 = 10x, x = 10	y2 + z2	(2x +20; y; z)	(x2 + y2; y2)	отрезок AB, A(2;0), B(0;2)

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ…………………………………………………….4

1. КРАТНЫЕ ИНТЕГРАЛЫ…………………………………..5

1.1. Двойные интегралы……………………………………….5

1.2. Тройные интегралы………………………………………13

2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ………………………21

2.1. Криволинейные интегралы первого рода……………….21

2.2. Криволинейные интегралы второго рода……………….23

3. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ……………………….29

3.1. Поверхностные интегралы первого рода………………..29

3.2. Поверхностные интегралы второго рода………………..36

4. ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ………………………44

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………..45

ПРИЛОЖЕНИЕ………………………………………………..46

ВВЕДЕНИЕ

В программу по высшей математике для большинства технических специальностей входит выполнение курсовой работы. Она приходится на третий семестр, когда студенты изучают кратные, криволинейные и поверхностные интегралы, а на их основе – теорию поля. Именно по этим разделам и составлена курсовая работа.

В курсовой работе требуется рассчитать технические параметры модели летательного аппарата. Подобные вычисления могут потребоваться при решении реальных инженерных задач, где необходимо исследовать оболочки или однородные объекты из различных материалов с точки зрения механики, а также воздействие внешних потоков среды или поля, что пересекается с задачами физики.

Сложность выполнения курсовой работы связана с необходимостью изучения большого объема материала из различных разделов высшей математики.

Методические указания содержат необходимые теоретические основы математики, особое внимание уделено физическим и техническим приложениям. Конечно, для более глубокого понимания теории потребуется изучение литературы, но все необходимые для курсовой работы определения и формулы в этих указаниях приведены. Дано много различных примеров с подробными решениями, часть рассматриваемых задач идентична заданиям курсовой работы, что облегчит ее выполнение.

Указания соответствуют уровню преподавания курса и могут быть использованы также и как конспект лекций.

КРАТНЫЕ ИНТЕГРАЛЫ

ДВОЙНЫЕ ИНТЕГРАЛЫ

Рис. 1.1

Пусть D - ограниченная замкнутая область в плоскости xOy. Функция z=f(x,y) определена и ограничена в области D (рис.1.1). Разобьем эту область на n частей и обозначим их площади соответственно ∆S₁, ∆S₂, ∆S₃, . . . , ∆S_n. В каждой части ∆S_i возьмем произвольно точку M_i (x_i, y_i) и составим сумму

. (1.1)

Эта сумма называется интегральной суммой функции f(x, y) в области D.

Определение. Если при любом разбиении области D на части ∆S_i и произвольном выборе точек M_i(x_i,y_i) существует предел последовательности сумм (1.1) при условии, что максимальный из диаметров частей ∆S_i стремится к нулю, то этот общий предел называют двойным интегралом от функции f(x, y) по области D и обозначают символом

.

Итак,

.

Область D называется областью интегрирования, а dS – элементом площади.

Свойства

Двойной интеграл обладает всеми основными свойствами обыкновенного интеграла функции одной переменной на отрезке.

1. Постоянный множитель можно выносить за знак двойного интеграла,

.

2. Двойной интеграл от суммы функций равен сумме двойных интегралов,

.

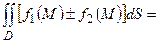
3. Область интегрирования можно разбить на части (рис.1.2),

.

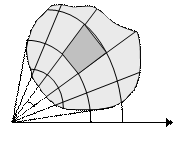
Геометрический смысл двойного интеграла

Если f(x, y) > 0, то двойной интеграл от функции f(x, y) по области D равен объему тела, ограниченного сверху поверхностью z = f(x, y), снизу плоскостью хОу и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости хОу область D,

.

Если f(x, y) = 1, то двойной интеграл равен площади области D, т.е.

.

Если в области D функция f(x, y) меняет знак, то область разбивается на две части: 1) область D₁, где f(x, y) > 0; 2) область D₂, где f(x, y) < 0. Предположим, что области D₁ и D₂ таковы, что двойные интегралы по этим областям существуют. Тогда интеграл по области D₁ будет положителен и равен объему тела, лежащему выше плоскости хОу. Интеграл по области D₂ будет отрицателен и по абсолютной величине равен объему тела, лежащего ниже плоскости хОу. Следовательно, интеграл по всей области D будет выражать разность этих объемов.

Вычисление двойного интеграла

1. В декартовых координатах элемент площади равен площади прямоугольника со сторонами dx и dy, т.е. dS =dxdy, тогда двойной интеграл записывают в виде

.

В общем случае область интегрирования сводится путем разбиения на части к двум основным видам.

Рис. 1.4

Первый вид - область D ограничена слева и справа прямыми х = a и х = b (a < b), а снизу и сверху - непрерывными кривыми y = y_(x) и y = y₂(x) (y₁(x) < y₂(x)). При этом каждая из кривых y₁(x) и y₂(x) пересекаются любой вертикальной прямой только в одной точке (рис.1.4). Для такой области двойной интеграл вычисляется по формуле:

. (1.2)

Последний интеграл называется двукратным и сначала вычисляется внутренний интеграл , в котором х считается постоянным, а затем вычисляется внешний интеграл по dx (пример 1.1), т.е.

.

Рис. 1.5

Второй вид - область D ограничена снизу и сверху прямыми y = c и y = d (c < d), а слева и справа - непрерывными кривыми x = x₁(y) и x = x₂(y) (x₁(y) < x₂(y)). При этом каждая из кривых x₁(y) и x₂(y) пересекаются любой горизонтальной прямой только в одной точке (рис.1.5). Для такой области справедлива формула:

2. Полярные координаты ρ и φ связаны с прямоугольными координатами х, у соотношениями

x = ρ cos φ, y = ρ sin φ.

ρdφ dS dφ   O dρ ρ

Элемент площади dS можно считать равным площади прямоугольника со сторонами dρ и ρdφ, последнее есть длина дуги окружности радиуса ρ с центральным углом dφ (рис.1.6), т.е.

dS = ρ dρ dφ,

тогдадвойной интеграл вычисляется по формуле

ρ cos φ, ρ sin φ) ρ dρ dφ.

Рис. 1.7

Если область интегрирования D ограничена лучами φ = α и φ = β (α<β) и двумя кривыми ρ = ρ₁(φ) и ρ = ρ₂(φ), где ρ₁(φ) и ρ₂(φ) - однозначные функции при α≤ φ ≤ β и ρ₁(φ)≤ρ₂(φ) (рис. 1.7), то двойной интеграл вычисляется по формуле:

ρ cos φ, ρ sin φ) ρ dρ(1.3)

(пример 1.2).